 |
Ответ: дом первого гнома. (6 баллов)
|
|
|
|
ОЛИМПИАДА ПО МАТЕМАТИКЕ 11 КЛАСС
Продолжительность 135 минут
Максимальное количество баллов - 22
1. Квадратный трехчлен 
не имеет корней и 
. Найдите знак коэффициента с.
(3 балла)
2. Два парома одновременно отходят от противоположных берегов реки и пересекают её перпендикулярно берегам. Скорости паромов постоянны, но не равны. Паромы встречаются на расстоянии 720 м от берега, после чего продолжают движение. На обратном пути они встречаются в 400 м от другого берега. Какова ширина реки?
(4 балла)
3. Последовательность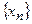 
определяется условиями: 
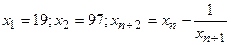. Докажите, что среди членов последовательности найдётся ноль. Найдите номер этого члена.
(4 балла)
4. Чему равна сумма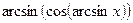 
и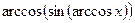 
?
(5 баллов)
5. Три гнома живут в разных домах на плоскости и ходят со скоростями 1, 2 и 3 км/ч соответственно. Какое место для ежедневных встреч нужно им выбрать, чтобы сумма времён, необходимых каждому из гномов на путь от своего дома до этого места (по прямой), была наименьшей?
(6 баллов)
РЕШЕНИЯ.
1. Квадратный трехчлен не имеет корней и . Найдите знак коэффициента с.
Решение:
Данный трехчлен не имеет корней, значит, его график не пересекает ось x. Так как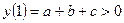 
, то график располагается в верхней полуплоскости, следовательно, 
.
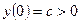Ответ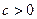 
. (3 балла)
2. Два парома одновременно отходят от противоположных берегов реки и пересекают её перпендикулярно берегам. Скорости паромов постоянны, но не равны. Паромы встречаются на расстоянии 720 м от берега, после чего продолжают движение. На обратном пути они встречаются в 400 м от другого берега. Какова ширина реки?
I решение. Суммарное расстояние, пройденное паромами к моменту первой встречи, равно ширине реки, а к моменту второй встречи равно утроенной ширине реки. Так как скорости паромов постоянны, то до второй встречи каждый из них пройдёт втрое большее расстояние, чем до первой встречи. Так как один из паромов до первой встречи прошёл 720 м, то до второй встречи он прошёл расстояние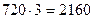 
м. При этом он прошёл путь, равный ширине реки, и ещё 400 м. Следовательно, ширина реки равна 2160 - 400 = 1760 м.
|
|
|
II решение. Пусть ширина реки равна S метров, а скорости паромов равны x и y. Тогда по условию задачи можно составить систему уравнений:
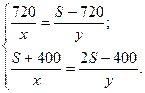
Разделим одно уравнение системы на другое, и после преобразований получаем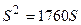 
, откуда S = 1760 (корень S = 0 - посторонний по смыслу задачи).
Ответ: 1760 метров. (4 балла)
3. Последовательность 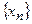определяется условиями: 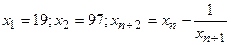. Докажите, что среди членов последовательности найдётся ноль. Найдите номер этого члена.
Решение:
Заметим, что если некоторый член этой последовательности равен нулю, то следующие члены не определены, так как в формуле для определения первого из них содержится деление на 0. Все дальнейшие рассуждения относятся к членам последовательности до этого нуля включительно (или к бесконечной последовательности, если нуля нет). После домножения правой и левой частей на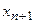 
имеем:
. Рассмотрим условие, при котором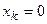 
. Он (k -ый член последовательности) равен нулю тогда и только тогда, когда:
;
;
……………………………………....
;
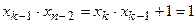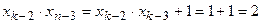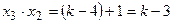Следовательно,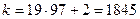 
.
Ответ 1845. (4 балла)
4. Чему равна сумма 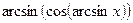и ?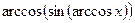
Решение:
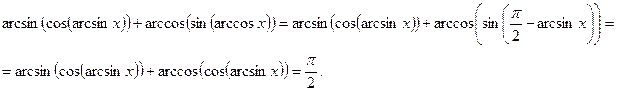
Ответ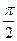 
. (5 баллов)
5. Три гнома живут в разных домах на плоскости и ходят со скоростями 1, 2 и 3 км/ч соответственно. Какое место для ежедневных встреч нужно им выбрать, чтобы сумма времён, необходимых каждому из гномов на путь от своего дома до этого места (по прямой), была наименьшей?
Решение:
Этим местом встречи является дом первого гнома (который ходит со скоростью 1 км/ч). Для доказательства этого обозначим искомое место встречи гномов буквой A, а дома занумеруем цифрами 1, 2, 3 в соответствии с величинами скоростей гномов. Расстояния между домом 1 и домами 2 и 3 обозначим через а и b, а расстояния от точки A до домов 1, 2, 3 - через x, y и z соответственно. Тогда
|
|
|
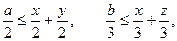
откуда
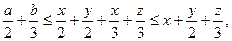
причём равенство достигается при х = 0, т. е. когда точка A совпадает с домом 1.
Ответ: дом первого гнома. (6 баллов)
|
|
|
