 |
Ответ: второй торговец. (5 баллов)
|
|
|
|
5. Один градус шкалы Цельсия равен 1,8 градусов шкалы Фаренгейта, при этом 0° по Цельсию соответствует 32° по шкале Фаренгейта. Может ли температура выражаться одинаковым числом градусов как по Цельсию, так и по Фаренгейту?
Решение: Из условия следует, что температура по Фаренгейту выражается через температуру по Цельсию следующим образом: TF = 1,8TC + 32o. Если TF = TC = x, то x = =1,8x + 32, то есть, x = -40.
Заметим, что корень уравнения можно было и не находить. Достаточно указать, что графики линейных функций с неравными угловыми коэффициентами пересекаются.
(5 баллов)
6. Треугольник АВС равнобедренный: АВ = ВС = 1, / ABC = 36o. Биссектрисы АK и СM пересекаются в точке О. Найдите периметр треугольника АМО.
Решение: Так как треугольник АВС - равнобедренный и / ABC = 36o, то / BАC = / BСA = 72o (см.рис.).
Так как АK и СM - биссектрисы треугольника, то 
ВАK = CAK = BCM = ACM = 36o. AВK = BAK, значит, 
АВК - равнобедренный (АК = ВК). АМС = СКА (по II признаку равенства треугольников), значит, АК = СM и СK = АМ, тогда, ВМ = ВК. АОС - равнобедренный, значит, АО = ОС, так как АК = МС, то МО = ОК.
Р АМО = АО + ОМ + АМ = АО + ОК + АМ = AK + AM = ВK + АМ = ВМ + АМ = АВ = 1.
Ответ: 1 (6 баллов)
ОЛИМПИАДА ПО МАТЕМАТИКЕ 7 КЛАСС
Продолжительность 135 минут
Максимальное количество баллов - 21
1. Таракан Кузьма объявил, что умеет бегать со скоростью 50 м/мин. Ему не поверили, и правильно: на самом деле Кузьма всё перепутал и думал, что в метре 60 сантиметров, а в минуте 100 секунд. С какой скоростью (в "нормальных" м/мин) бегает таракан Кузьма?
(3 балла)
2. У двузначного числа первая цифра вдвое больше второй. Если к этому числу прибавить квадрат его первой цифры, то получится квадрат некоторого целого числа. Найдите исходное двузначное число.
|
|
|
(3 балла)
3. Пять футбольных команд провели турнир - каждая команда сыграла с каждой по разу. За победу начислялось 3 очка, за ничью - 1 очко, за проигрыш очков не давалось. Четыре команды набрали соответственно 1, 2, 5 и 7 очков. А сколько очков набрала пятая команда? (4 балла)
4. В числах МИХАЙЛО и ЛОМОНОСОВ каждая буква обозначает цифру (разным буквам соответствуют разные цифры). Известно, что у этих чисел произведения цифр равны. Могут ли оба числа быть нечётными? (5 баллов)
5. Четырёхугольник с длинами сторон 1, 1, 1 и 2 имеет две параллельные стороны и разбит на четыре одинаковые фигуры (см. рисунок). В результате верхняя сторона разделилась на четыре отрезка. Найдите отношение длины большего отрезка к меньшему.
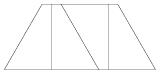
(6 баллов)
РЕШЕНИЯ.
1. Таракан Кузьма объявил, что умеет бегать со скоростью 50 м/мин. Ему не поверили, и правильно: на самом деле Кузьма всё перепутал и думал, что в метре 60 сантиметров, а в минуте 100 секунд. С какой скоростью (в "нормальных" м/мин) бегает таракан Кузьма?
Ответ. 18 м/мин.
Решение. Кузьма пробегает 50*60=3000 см за 100 с, то есть его скорость 30 см/с, что составляет 18 м/мин. (3 балла)
2. У двузначного числа первая цифра вдвое больше второй. Если к этому числу прибавить квадрат его первой цифры, то получится квадрат некоторого целого числа. Найдите исходное двузначное число.
Решение
Первая цифра в два раза больше второй только у следующих двузначных чисел: 21, 42, 63 и 84. Проверкой убеждаемся, что условию задачи удовлетворяет только число 21.
Ответ: 21 (3 балла)
3. Пять футбольных команд провели турнир - каждая команда сыграла с каждой по разу. За победу начислялось 3 очка, за ничью - 1 очко, за проигрыш очков не давалось. Четыре команды набрали соответственно 1, 2, 5 и 7 очков. А сколько очков набрала пятая команда?
Ответ. 12 очков
Решение. Каждая команда провела 4 игры. Ясно, что первая команда один раз сыграла вничью, а остальные игры проиграла. Вторая имеет две ничьи и два поражения. Третья команда пять очков на одних ничьих набрать не могла, стало быть, она один раз выиграла, кроме того, у неё две ничьи и поражение. Четвёртая команда победила два раза (если бы один, то ей пришлось бы набрать в трёх играх на одних ничьих 4 очка, что невозможно). Также у этой команды есть ничья и поражение. В итоге первые четыре команды выиграли 3 раза, а проиграли 7 раз. Однако число побед должно равняться числу поражений. Значит, 4 раза они проиграли пятой команде, и у той 12 очков. Нетрудно привести пример турнира, где такое распределение очков возможно. Пусть пятая команда выиграла у всех, четвёртая - у первой и второй, третья - у первой, а все остальные игры закончились вничью. Тогда у каждой команды будет названное число очков. (4 балла)
|
|
|
4. В числах МИХАЙЛО и ЛОМОНОСОВ каждая буква обозначает цифру (разным буквам соответствуют разные цифры). Известно, что у этих чисел произведения цифр равны. Могут ли оба числа быть нечётными?
Ответ. Нет.
Решение. Заметим, что использованы 10 различных букв, поэтому каждая цифра обозначена какой-нибудь буквой, в частности, среди этих цифр есть нуль. Таким образом, произведение цифр одного (а значит, и второго) числа равно нулю. Следовательно, в записи обоих чисел есть нуль. В словах МИХАЙЛО и ЛОМОНОСОВ общие буквы М, Л и О, поэтому нуль обозначает одна из них. Это не могут быть Л и М, поскольку числа не могут начинаться с нуля. Значит, нуль обозначен буквой О. В числе МИХАЙЛО на конце нуль, то есть оно чётное. (5 баллов)
5. Четырёхугольник с длинами сторон 1, 1, 1 и 2 имеет две параллельные стороны и разбит на четыре одинаковые фигуры (см. рисунок). В результате верхняя сторона разделилась на четыре отрезка. Найдите отношение длины большего отрезка к меньшему.
Решение
Пусть x — длина меньшего отрезка. В верхней стороне четырёхугольника, имеющей длину 1, укладывается 3 маленьких отрезка и один большой. Значит, длина большого отрезка равна 1 - 3 x. В нижней стороне четырёхугольника, имеющей длину 2, укладывается 3 больших отрезка и один маленький. Получаем уравнение
3. (1 - 3 x) + x = 2. Отсюда 3 - 9 x + x = 2. Следовательно, x = 
.
|
|
|
Итак, длина меньшего отрезка равна 1/8. Поэтому длина большего равна 1 - 3. 1/8 = 1 - 3/8 = 5/8. Значит, больший отрезок в пять раз длиннее меньшего.
Ответ. 5 (6 баллов)
|
|
|
