 |
Олимпиадная работа по математике 6 класс
|
|
|
|
Продолжительность - 90 минут
Максимальное количество баллов - 30
1. На острове Буяне 4 государства. Каждое из них граничит с тремя другими. Нарисуйте карту этого острова, если три государства имеют выход к морю.
(2 балла)
2. Имеются двое песочных часов: на 3 минуты и на 7 минут. Яйцо варится 11 минут. Как отмерить это время при помощи имеющихся часов?
(3 балла)
3. Прямоугольник составлен из шести квадратов. Найдите сторону самого большого квадрата, если сторона самого маленького равна 1.
 |
(4 балла)
4. Одному участнику игры было предложено 30 вопросов. За каждый правильный ответ ему начисляют 7 баллов, а за неправильный снимают 12 баллов. Сколько верных ответов дал участник игры, если он набрал 77 баллов.
(4 балла)
5. В двузначном числе десятков втрое больше чем единиц. Если от этого числа отнять число, записанное теми же цифрами, но в обратном порядке то получиться 36. Найти это число.
(5 баллов)
6. Какой цифрой оканчивается число 22010
(6 баллов)
7. Таракан Кузьма объявил, что умеет бегать со скоростью 50 м/мин. Ему не поверили, и правильно: на самом деле Кузьма всё перепутал и думал, что в метре 60 сантиметров, а в минуте 100 секунд. С какой скоростью (в "нормальных" м/мин) бегает таракан Кузьма?
(6 баллов)
РЕШЕНИЯ.
1. На острове Буяне 4 государства. Каждое из них граничит с тремя другими. Нарисуйте карту этого острова, если три государства имеют выход к морю.
Решение. Море
(2 балла)
2. Имеются двое песочных часов: на 3 минуты и на 7 минут. Яйцо варится 11 минут. Как отмерить это время при помощи имеющихся часов?
Решение. Перевернуть обои часы. Когда пройдет 3 минуты, в семиминутных часах останется 4 минуты. Поставить яйцо в данный момент вариться. Когда 4 минуты закончатся, перевернуть семиминутные часы обратно. Получим 4 + 7 = 11.
|
|
|
Ответ: 11 (3 балла)
3. Прямоугольник составлен из шести квадратов. Найдите сторону самого большого квадрата, если сторона самого маленького равна 1.
|
Обозначим длину стороны самого большого квадрата за а. Тогда двигаясь от большого квадрата по часовой стрелке, последовательно выразим через а стороны других квадратов: а-1, а-2, а-3. Из равенства верхней и нижней сторон прямоугольника получаем уравнение а + (а – 1) = (а - 2) + (а - 3) + (а - 3). Корнем данного уравнения является число 7. Тогда сторона большого квадрата равна 7.
Ответ: 7 (4 балла)
4. Одному участнику игры было предложено 30 вопросов. За каждый правильный ответ ему начисляют 7 баллов, а за неправильный снимают 12 баллов. Сколько верных ответов дал участник игры, если он набрал 77 баллов.
Решение. Пусть х число верных ответов, тогда (30 – х) число неверных ответов. 7х очков начисляют за верный ответ, тогда 12(30 – х) очков за неверный ответ. Всего участник набрал 77 очков. Получаем уравнение: х – 12(30 – х) = 77. Откуда х = 23.
Ответ: 23 верных ответа. (4 балла)
5. В двузначном числе десятков втрое больше чем единиц. Если от этого числа отнять число, записанное теми же цифрами, но в обратном порядке то получиться 36. Найти это число.
Решение. Пусть х – число единиц, 3х – число десятков, тогда число: 3х∙10 + х, «обратное число» х∙10+3х 30х + х – 10х + 3х = 36 Из уравнения получаем: х = 2. 2 – число единиц, 6 число десятков. Тогда число – 62.
Ответ: 62. (5 баллов)
6. Какой цифрой оканчивается число 22010
Решение. 2 
= 2, 2 
= 4, 2 
=8, 2 
=16, 2 
=32, 2 
=64 и т.д. Замечаем закономерность, что цифры 2,4,8,6 дальше повторяются. 2010=502∙4+2, значит, 2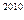 
оканчивается той же цифрой, что и 2 , то есть цифрой 4.
Ответ: 4 (6 баллов)
7. Таракан Кузьма объявил, что умеет бегать со скоростью 50 м/мин. Ему не поверили, и правильно: на самом деле Кузьма всё перепутал и думал, что в метре 60 сантиметров, а в минуте 100 секунд. С какой скоростью (в "нормальных" м/мин) бегает таракан Кузьма?
|
|
|
Ответ. 18 м/мин.
Решение. Кузьма пробегает 50*60=3000 см за 100 с, то есть его скорость 30 см/с, что составляет 18 м/мин.
Ответ: 18. (6 баллов)
ОЛИМПИАДА ПО МАТЕМАТИКЕ 5 КЛАСС
|
|
|
