Олимпиада по математике 10 класс

Продолжительность 135 минут

Максимальное количество баллов - 29

 

1. Барон Мюнхгаузен рассказывал, что у него есть карта страны Оз с пятью городами. Каждые два города соединены дорогой, не проходящей через другие города. Каждая дорога пересекает на карте не более одной другой дороги (и не более одного раза). Дороги обозначены желтым или красным (по цвету кирпича, которым вымощены), и при обходе вокруг каждого города (по периметру) цвета выходящих из него дорог чередуются. Могут ли слова барона быть правдой? Решение задачи можно представить чертежом.

(3 балла)

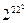2. Расположите в порядке возрастания числа: 222 ; 22²²; 2²²²; ; ; . Ответ обоснуйте.

(4 балла)
3. Корни уравнения x ² + ax + 1 = b - целые, отличные от нуля, числа. Докажите, что число

a ²+ b ² является составным.
(5 балла)

4. На сторонах AB и AC треугольника ABC нашлись такие точки M и N, отличные от вершин, что MC=AC и NB=AB. Точка P симметрична точке A относительно прямой BC. Докажите, что PA является биссектрисой угла MPN.

(5 баллов)

5. Три гнома живут в разных домах на плоскости и ходят со скоростями 1, 2 и 3 км/ч соответственно. Какое место для ежедневных встреч нужно им выбрать, чтобы сумма времён, необходимых каждому из гномов на путь от своего дома до этого места (по прямой), была наименьшей?

(6 баллов)

6. Графики функций у = х² + ах + b и у = х² + сх + d пересекаются в точке с координатами (1; 1). Сравните a ⁵ + d ⁶ и c⁶- b⁵.

(6 баллов)

 

РЕШЕНИЯ.

1. Барон Мюнхгаузен рассказывал, что у него есть карта страны Оз с пятью городами. Каждые два города соединены дорогой, не проходящей через другие города. Каждая дорога пересекает на карте не более одной другой дороги (и не более одного раза). Дороги обозначены желтым или красным (по цвету кирпича, которым вымощены), и при обходе вокруг каждого города (по периметру) цвета выходящих из него дорог чередуются. Могут ли слова барона быть правдой?

Решение

Пример изображен на рисунке:

 

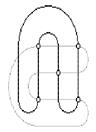
Ответ: могут. (3 балла)

 

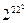2. Расположите в порядке возрастания числа: 222 ; 22²²; 2²²²; ; ; . Ответ обоснуйте.
Решение:

Сначала рассмотрим показатели степеней с основанием 2 и сравним их: = 2⁴ = 16 < 222 < 22² = 484 < 512 = 2⁹ < 2²². Следовательно, < 2²²² < < .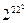
Затем оценим остальные степени: = 22⁴ > 16⁴ = 2¹⁶ = и = 22⁴ < 22²² < 64³⁷ = (2⁶) = 2²²²; 222² < 256² = 2¹⁶ = .
Ответ:

222² < < 22² < 22²² < 2²²² < 2 < 2 . (4 балла)

 

3. Корни уравнения x ² + ax + 1 = b - целые, отличные от нуля, числа. Докажите, что число

a ² + b ² является составным.

Решение: Запишем данное квадратное уравнение в стандартном виде: x ² + ax + (1 - b) = 0. По теореме Виета: x ₁ + x ₂ = - a, x ₁^. x ₂ = 1 - b, где x ₁ и x ₂ — корни данного уравнения. Значит, a = - (x ₁ + x ₂), b = 1 - x ₁^. x ₂. Следовательно, a ² + b ² = (x ₁ + x ₂)² + (1 - x ₁^. x ₂)² = x ₁² + x ₂² + 1 + x ₁^2. x ₂² = (x ₁² + 1) (x ₂² + 1). Полученное число является составным, так как, если x ₁ и x ₂ — целые, то каждый из множителей принимает целое значение, отличное от единицы.

(5 баллов)

4. На сторонах AB и AC треугольника ABC нашлись такие точки M и N, отличные от вершин, что MC=AC и NB=AB. Точка P симметрична точке A относительно прямой BC. Докажите, что PA является биссектрисой угла MPN.

 

Решение.

 

Из равенства MC=AC вытекает, что AMC = BAC, а из симметрии следует, что BPC = BAC. Отсюда BPC + BMC = BAC +(180^o - AMC) = 180^o, поэтому четырехугольник BMCP – вписанный. Отсюда MPA= MPC- APC= MBC PAC= ABC-(90^o- ACB)= ABC+ ACB-90^o Аналогично, NPA= ABC+ ACB-90^o.

Замечание. Еще одно решение можно получить как следствие известного факта о том, что высоты треугольника ABC являются биссектрисами треугольника с вершинами основаниях высот: при гомотетии с центром A и коэффициентом точки P, N и M переходят в основания высот треугольника ABC. (5 баллов)

 

5. Три гнома живут в разных домах на плоскости и ходят со скоростями 1, 2 и 3 км/ч соответственно. Какое место для ежедневных встреч нужно им выбрать, чтобы сумма времён, необходимых каждому из гномов на путь от своего дома до этого места (по прямой), была наименьшей.

Решение:

Этим местом встречи является дом первого гнома (который ходит со скоростью 1 км/ч). Для доказательства этого обозначим искомое место встречи гномов буквой A, а дома занумеруем цифрами 1, 2, 3 в соответствии с величинами скоростей гномов. Расстояния между домом 1 и домами 2 и 3 обозначим через а и b, а расстояния от точки A до домов 1, 2, 3 - через x, y и z соответственно. Тогда

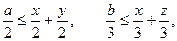
откуда

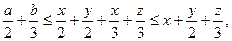
причём равенство достигается при х = 0, т. е. когда точка A совпадает с домом 1.

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: