Выявление взаимосвязи исследуемых признаков

Количественные признаки:

· если признаки измерены в шкале интервалов или отношений и распределились нормально, то применим коэффициент корреляции Пирсона r_xy.

Примечание: для больших выборок от 5 человек и более. Значения признаков должны быть распределены нормально.

· если признаки измерены в порядковой (ранговой) шкале, шкале интервалов или отношений, то применим коэффициент корреляции Спирмена r_s.

Примечание: для малых выборок обычно 5≥n≥40

· Если признаки измерены в порядковой (ранговой) шкале, то применим коэффициент корреляции Кендалла τ.

Примечание: не допускается использование одинаковых рангов.

Качественные признаки:

· если признаки измерены в дихотомической шкале, то применим коэффициент ассоциации Пирсона φ;

· если один признак измерен в дихотомической шкале, а другой в ранговой шкале, то применим рангово-бисериальный коэффициент корреляции R_rb;

· если один признак измерен в дихотомической шкале, а другой в шкале отношений или интервалов, то применим бисериальный коэффициент корреляции R_бис.

 

Выявление структуры взаимосвязей признаков:

· метод максимального корреляционного пути Л.К. Выханду (структура с доминирующими и подчиненными признаками);

· метод усредненного рангового места коэффициента корреляции (выявляет признаки, имеющие наибольший удельный вес в структуре взаимосвязей);

· метод корреляционных плеяд;

· метод факторного анализа (сокращение числа переменных [редукция данных] и определение структуры взаимосвязей, классификация переменных. Метод структурной классификации.)

 

 

Выявление влияния отдельных факторов на результаты экспериментов:

· дисперсионный анализ (анализ изменчивости признака под влиянием каких-либо контролируемых переменных факторов, т.е. выявление причинно-следственной связи);

· регрессионный анализ (функциональная, чаще линейная зависимость одного признака от другого или нескольких признаков);

· корреляционное отношение (вклад одних признаков в общее влияние всех признаков, воздействующих на коррелируемый признак – показатель уровня связи, употребляющийся в случае нелинейной зависимости между признаками).

Нулевая гипотеза (обозначается Н₀) предполагает, что в эксперименте не будет выявлено различий. Например: «Между учениками 1 класса А и 1 класса Б нет различий по уровню интеллекта».

Альтернативная гипотеза (обозначается Н₁) предполагает, что будут выявлены различия (что различия будут достоверны). Например: «Ученики 1 класса А и 1 класса Б отличаются по уровню интеллекта».

Гипотезы также могут быть ненаправленными (см. предыдущий пример) и направленными: «Ученики 1 класса А превосходят по уровню интеллекта учеников 1 класса Б».

Уровни статистической значимости

Статистическая значимость (p-уровень) представляет собой оцененную меру уверенности в его «истинности». Более высокий уровень значимости соответствует более низкому уровню доверия к полученным результатам.

В психологии обычно используется три уровня значимости:

5-процентный, 1-процентный и 0,1- процентный (хотя последний намного реже). Если указывают, что различия достоверны на 5%-ом уровне значимости (p < 0.05), то имеют ввиду, что вероятность ошибочного вывода составляет 0,05, если на 1%-ом, то – 0,01 (p < 0.01) и т.д. При этом 5%-й уровень считается низшим, а 0,1%-й – высшим уровнем значимости (p < 0.001).

Различают эмпирическое значение критерия и его критическое значение. При использовании большинства критериев, если эмпирическое значение больше критического, то H₀ отвергается.

 

Алгоритм математико-статистической обработки результатов

Психологического исследования

1. Сформулировать исследовательскую задачу.

2. Оценить размер выборки, характер распределения значений и выбрать параметрический или непараметрический метод (критерий).

3. Сформулировать нулевую и альтернативную гипотезы исследования.

4. Вычислить эмпирическое значение критерия.

5. В справочной таблице найти критические значения критерия.

6. Сопоставить эмпирическое значение с критическими и сделать вывод о принятии или опровержении гипотез исследования

Алгоритм ранжирования

1. Меньшему значению начисляется меньший ранг. Наименьшему значению начисляется ранг 1. Наибольшему значению начисляется ранг, соответствующий количеству ранжируемых значений. Например, если n=7, то наибольшее значение получит ранг 7, за возможным исключением тех случаев, которые предусмотрены правилом 2.

2. Если несколько значений равны, то им начисляется ранг, представляющий собой среднее значение из тех рангов, которые они получили бы, если бы не были равны. Например, три наименьших значения равны десяти. Если бы время измеряли более точно, то эти значения могли бы различаться и составляли бы, скажем, 10,2 с, 10,5 с, 10,7 с. В этом случае они получили бы ранг 1, 2 и 3 соответственно. Но поскольку полученные значения равны, каждое из них получает средний ранг: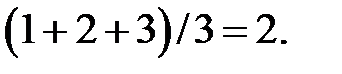

3. Общая сумма рангов должна совпадать с расчетной, которая определяется по формуле:

где N – общее количество ранжируемых наблюдений (значений). Несовпадение реальной и расчетной сумм рангов будет свидетельствовать об ошибке, допущенной при начислении рангов или их суммировании. Прежде чем продолжить работу, необходимо найти ошибку и устранить ее.

 

⇐ Предыдущая45678910111213Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: