Математические модели притока к горизонтальному стволу скважины

 

При стационарной фильтрации однофазного флюида (нефти или газа) задача сводится к решению уравнения Лапласа относительно функции Лейбензона. Одно их частных решений этого уравнения было получено Б. Риманом в виде функции:

, (1.23)

где - постоянные.

В случае притока однофазного флюида к точечному стоку это решение может быть представлено в виде:

, (1.24)

где 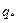- массовый расход флюида (нефти и газа), - значение функции Л.С. Лейбензона на контуре питания.

В случае если сток является отрезком линии равных стоков, то решение может быть получено путем прямого интегрирования этого уравнения по переменным , которые представляют собой текущие координаты точек на линии равных стоков. В частности, если линия равных стоков есть отрезок координатной оси «ох» , то находим для нефти

, (1.25)

где - значение давления в точках и .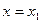

 

Соответственно для газа имеем

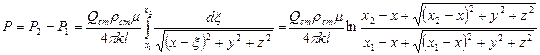,(1.26)

где - функция Лейбензона, - плотность нефти и объемный дебит нефтяной скважины; для газа - плотность газа и объемный дебит газовой скважины, приведенные к нормальным и стандартным условиям, - длина горизонтального ствола.

Рассмотрим линию равных стоков с началом в центре системы координат, то есть в точке (0,0,0) и концом в точке (,0,0). После интегрирования предыдущего уравнения получаем для нефти

, (1.27)

соответственно для газа получаем

, (1.28)

где .

Для оценки характера изменения давления нефти или функции Л.С.Лейбензона для горизонтального ствола введем функцию для нефти и функцию для газа. Эта функция на стенке горизонтального ствола, то есть пр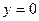и и , в соответствии с предыдущим уравнением, принимает значения

. (1.29)

В последних работах по обработке результатов интерференции горизонтальных скважин, показано, что представление о скважине, как о линии равных стоков, дает хорошую основу для решения обратных задач, в частности, определения работающей длины горизонтального ствола [15].

Подводя итоги по рассмотрению проблем расчета дебитов и продуктивности, Д.К. Бабу высказал мнение, что «ни бесконечная проводимость, ни равномерность притока не адекватны пластовым условиям. В этом контексте может быть очень полезно теоретическое решение следующей задачи. Совместное рассмотрение течения в пласте и стволе есть наиболее общий подход. Необходимо совместно использовать уравнения течения в пласте по закону Дарси и уравнения Навье-Стокса для движения флюида в горизонтальном стволе. Эта система решается для определения давления и потока вдоль и вокруг скважины».

Гидродинамические основы этого подхода к расчету дебита горизонтальных скважин изложены в работах В.А. Черных. Проведенные исследования позволили разработать методику оценки влияния потерь давления в горизонтальном стволе на результаты стационарных гидродинамических исследований [93,94].

При малых депрессиях на пласт в скважинах с высокой производительностью - падение давления в горизонтальном стволе может быть существенным. При этом допущение о равенстве давлений или притоков вдоль горизонтального ствола скважины является некорректным. Таким образом, при обработке результатов стационарных исследований горизонтальных скважин может быть установлена корректность допущения о равенстве давлений или притоков вдоль горизонтального ствола. Для этого необходимо решить систему уравнений притока флюида и движения его в горизонтальном стволе. Соответствующая функция влияния потерь давления в горизонтальном стволе скважины имеет вид

; (1.30)

, (1.31)

где - коэффициент гидравлического сопротивления горизонтального ствола; 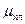- динамическая вязкость флюида в пластовых условиях; - проницаемость; - длина горизонтального ствола; - радиус горизонтального ствола и контура питания соответственно.

В случае фильтрации по закону Дарси все уравнения притока однофазного флюида как к одиночной горизонтальной, так и к многоствольной скважине имеют общую форму:

- для нефти

; (1.32)

- для газа

, (1.33)

где - давление, - функция Лейбензона, 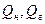- массовый дебит нефти и газа, , , - функция, зависящая только от геометрических параметров пласта и скважины, - длина горизонтального ствола.

 

Математические модели притока к радиальной системе горизонтальных скважин. Самое первое и наиболее простое уравнение притока флюида к радиальной системе горизонтальных скважин было получено Д.Читрини путем представления стволов к щелям и сведения пространственной фильтрации к плоскорадиальному потоку. С помощью этого допущения и применения конформных отображений удалось получить формулу для определения радиуса эквивалентной по производительности совершенной скважины, заменяющей систему щелей (трещин)

, (1.34)

где - длина горизонтального ствола, - число горизонтальных стволов.

При этом суммарный массовый дебит всех горизонтальных стволов предлагается рассчитывать по формуле Дюпюи

, (1.35)

где 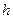- толщина пласта, - радиус контура питания, - значение потенциала скорости на контуре питания и в горизонтальном стволе.

Как показывает анализ, результат Д. Читрини приводит к значительному завышению дебита радиальной системы горизонтальных скважин, так как в представленном решении отсутствует хотя бы приближенное приведение вертикальных щелей (трещин) к реальным горизонтальным скважинам. Способ Д. Читрини с какой-то степенью приближения применим лишь в случае очень большой длины горизонтальных стволов по сравнению с толщиной продуктивного пласта [28].

Строгое решение задачи, учитывающее изменение интенсивности притока по длине горизонтального ствола, было получено Д.Кокки, но оно оказалось очень громоздким и малопригодным для практических расчетов.

Первое аналитическое решение задачи о притоке однофазного флюида к радиальной системе горизонтальных скважин было получено Полубариновой-Кочиной для полупространства, на верхней границе которого задано давление [15].

Но решение данной задачи может иметь некоторое практическое применение только для пластов очень большой толщины или при расположении горизонтальных стволов непосредственно вблизи верхней или нижней границы (кровли или подошва) пласта.

С практической точки зрения больший интерес представляет решение для пласта конечной толщины. Если горизонтальные скважины равномерно расположены симметрично относительно кровли и подошвы пласта под углами между собой, то понижение потенциала на скважине с углом 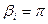будет равно (Г.А Разумов 1962г.)

. (1.36)

Соответственно выражение для дебита -го горизонтального ствола имеет вид

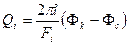, (1.37)

где

. (1.38)

 

Дебит радиальной системы горизонтальных скважин, расположенной несимметрично относительно кровли и подошвы пласта, можно определить по формуле

, (1.39)

где коэффициент определяется по табл. 1.1

Таблица 1.1

Определение коэффициента .

 

		0,10	0,25	0,50
1,0	0,30	0,70	0,89	1,0
2,5	0,40	0,75	0,91	1,0
5,0	0,45	0,80	0,93	1,0
7,5	0,50	0,825	0,94	1,0
10,0	0,53	0,85	0,95	1,0

 

где - вертикальная координата оси горизонтального ствола, отсчитываемая от кровли или подошвы пласта, 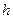- толщина пласта, - длина горизонтального ствола.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: