 |
Применение теории потенциала для решения задач установившегося притока жидкости к горизонтальной скважине
|
|
|
|
Потенциал точечного стока, горизонтальной дрены и несовершенной галереи в полосообразном однородно-анизотропном пласте. Здесь рассматривается приток к точечному стоку с координатами 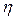 и
и  [27], расположенному несимметрично в полосообразном горизонтальном однородно-анизотропном пласте с подошвенной водой (рис. 1.1).
[27], расположенному несимметрично в полосообразном горизонтальном однородно-анизотропном пласте с подошвенной водой (рис. 1.1).

Рис. 1.1. Схема притока к точечному стоку, горизонтальной скважины и несовершенной щели в полосообразном пласте
 , (1.1)
, (1.1)
где  и
и  - функции Дирака,
- функции Дирака,  - плотность точечного стока.
- плотность точечного стока.
Введем потенциал [28]:
 , (1.2)
, (1.2)
и характеристику анизотропного пласта:
 , (1.3)
, (1.3)
где  - проницаемость по горизонтали,
- проницаемость по горизонтали, 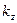 - проницаемость по вертикали.
- проницаемость по вертикали.
Тогда уравнение (1.1) принимает вид [28]:
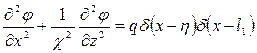 . (1.4)
. (1.4)
Кровля и подошва (первоначальная граница раздела) считаются непроницаемыми, то есть имеем:
 при
при  ,
,  . (1.5)
. (1.5)
На контуре питания для простоты принимается:
 при
при  ,
, 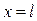 . (1.6)
. (1.6)
Уравнение (1.4) с граничными условиями (1.5) и (1.6) можно решить методом интегральных преобразований, применяя последовательно косинус-преобразование и синус-преобразование Фурье с конечными пределами и формулы обращения. Такое решение получается в виде [28, 32]:
 ; (1.7)
; (1.7)
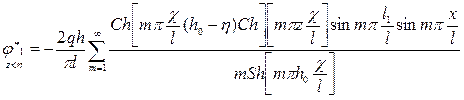 . (1.8)
. (1.8)
Формула (1.7) и (1.8) дают распределение потенциала, вызванного точечными стоками или источником в элементе анизотропного полосообразного пласта. Их можно использовать при экспериментировании на щелевом лотке и для горизонтальной дрены.
Можно получить потенциал и для несовершенной щели (трещины гидравлического разрыва пласта) в том же пласте. При этом щель будем рассматривать как линию стоков, расположенных вдоль прямой х=l1 от z=0 до z=b, при постоянной мощности стока q (рис. 1.1). Тогда потенциал линии стоков определится интегралом [28]:
|
|
|
 . (1.9)
. (1.9)
Подставляя (1.7) и (1.8) в (1.9), интегрируя последнее уравнение и делая некоторые преобразования, получаем [28]:
 ; (1.10)
; (1.10)
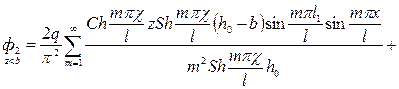

(1.11)
Если b=h0, то из формулы (1.11) получается выражение для потенциала совершенной щели (трещины) в полосообразной залежи:
 (1.12)
(1.12)
Если за высоту горизонтальной дрены принять длину горизонтальной скважины с=πd, произвольно расположенной в пласте, то потенциал такой дрены на единицу ширины потока определится интегралом [28]:
 ; (1.13)
; (1.13)

 ; (1.14)
; (1.14)
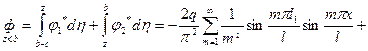
 . (1.15)
. (1.15)
Для вывода формулы для дебита горизонтальной скважины необходимо усреднить потенциал (1.15) (по диаметру  ) в вертикальном направлении на отрезке линии стоков, равном длине окружности
) в вертикальном направлении на отрезке линии стоков, равном длине окружности  в соответствии с конвергенцией трещины. Введем следующие безразмерные параметры [28]:
в соответствии с конвергенцией трещины. Введем следующие безразмерные параметры [28]:
 (1.16)
(1.16)
Вводя в формулу (1.15) потенциал Ф0 на контуре x=1, определяем усредненный потенциал на отрезке линии стоков:
 . (1.17)
. (1.17)
Внося уравнение (1.15) в (1.17), учитывая (1.16), производя интегрирование и переходя от потенциала к давлению, получаем следующую формулу дебита горизонтальной скважины для одностороннего притока [28]:
 (1.18)
(1.18)
 (1.19)
(1.19)
 . (1.20)
. (1.20)
Для двухстороннего притока в формулах (1.19) и (1.20) следует принять:  .
.
Дебит вертикальной гидравлической трещины определяется по формуле [28]:
 , (1.21)
, (1.21)
где 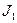 и
и  - фильтрационные сопротивления определяемые по формулам (1.19) и (1.20) при
- фильтрационные сопротивления определяемые по формулам (1.19) и (1.20) при  ,
,  -проницаемость вдоль напластования,
-проницаемость вдоль напластования,  – длина горизонтальной скважины или протяженность трещины в горизонтальном положении.
– длина горизонтальной скважины или протяженность трещины в горизонтальном положении.
Оценка погрешности формул (1.19) и (1.20) показала, что она зависит от параметра  и числа принятых членов n в бесконечных рядах. Так, при
и числа принятых членов n в бесконечных рядах. Так, при  (сильно анизотропные пласты), при n=1 погрешность составляет не более 0,19%; при
(сильно анизотропные пласты), при n=1 погрешность составляет не более 0,19%; при  и
и  погрешность
погрешность  . Поэтому, для практических расчетов в приведенных рядах достаточно удержать не более
. Поэтому, для практических расчетов в приведенных рядах достаточно удержать не более  члена при
члена при  .
.
В заключение отметим, решения (1.11) и (1.14) успешно могут быть использованы в теории конусообразования для расчета предельных безводных и безгазовых дебитов и депрессии при дренировании продуктивных пластов горизонтальными и «несовершенными» вертикальными трещинами ГРП.
|
|
|
Если за горизонтальную дрену принять горизонтальную скважину диаметром  , произвольно расположенную в пласте (рис.1.1), то дебит скважины (при
, произвольно расположенную в пласте (рис.1.1), то дебит скважины (при 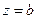 и
и  ) выразится приближенной формулой [28]:
) выразится приближенной формулой [28]:
 (1.22)
(1.22)
где

 (1.23)
(1.23)
 (1.24)
(1.24)
где  – проницаемость пласта вдоль напластования,
– проницаемость пласта вдоль напластования,  – продуктивная толщина пласта,
– продуктивная толщина пласта,  – длина горизонтальной скважины,
– длина горизонтальной скважины,  – длина пласта,
– длина пласта,  – давление на границе пласта (на контуре питания),
– давление на границе пласта (на контуре питания),  – давление на забое скважины,
– давление на забое скважины, 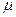 - динамическая вязкость нефти,
- динамическая вязкость нефти,  – расстояние от кровли до положения горизонтальной скважины,
– расстояние от кровли до положения горизонтальной скважины,  - коэффициент анизотропии,
- коэффициент анизотропии, 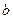 – вертикальная проницаемость.
– вертикальная проницаемость.
Если скважина расположена симметрично относительно области дренирования, то в формуле (1.22) следует принять 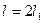 .
.
Формула (1.21) справедлива для расчета дебита горизонтальной скважины с открытым забоем и может быть использована для обработки индикаторных линий. В условиях перфорированной колонны следует использовать формулу приведенного радиуса скважины, в которой добавочные фильтрационные сопротивления С0 можно определить по формуле [28]:
 . (1.25)
. (1.25)
где  – длина перфорированного канала радиуса
– длина перфорированного канала радиуса 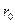 ,
,  – число каналов на погонный метр.
– число каналов на погонный метр.
Пласт однородно-анизотропный полубесконечный. Для полубесконечного пласта можно получить наиболее простое приближенное решение задачи, если воспользоваться методом зеркального бесконечного отображения точечного стока (источника) в кровлю и подошву пласта.
Многократно отражая скважину-сток с интенсивностью  в кровлю и подошву, получаем две бесконечные цепочки: скважин-стоков и скважин-источников с координатами
в кровлю и подошву, получаем две бесконечные цепочки: скважин-стоков и скважин-источников с координатами  ,
,  (рис. 1.1). Суперпозиция полей двух таких цепочек дает потенциал, который для однородной пористой среды определяется выражением [6]:
(рис. 1.1). Суперпозиция полей двух таких цепочек дает потенциал, который для однородной пористой среды определяется выражением [6]:

 . (1.26)
. (1.26)
С целью получения постоянства потенциала  на контуре
на контуре  , через которую проходит ось Z, отобразим все скважины полученных двух бесконечных цепочек на ось Z и возьмем величину
, через которую проходит ось Z, отобразим все скважины полученных двух бесконечных цепочек на ось Z и возьмем величину  с обратным знаком. Таким образом, получаются еще две равнодебитные бесконечные цепочки, являющиеся зеркальным отображением первых двух относительно оси Z.
с обратным знаком. Таким образом, получаются еще две равнодебитные бесконечные цепочки, являющиеся зеркальным отображением первых двух относительно оси Z.
|
|
|
Результат суперпозиции полей последней пары бесконечных цепочек выражается формулой [28]:
 .(1.27)
.(1.27)
Результирующий потенциал, очевидно, запишется в форме 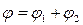 :
:
 .(1.28)
.(1.28)
Постоянная интегрирования  определяется из граничного условия: при
определяется из граничного условия: при
 . Из формулы (1.28) следует, что
. Из формулы (1.28) следует, что
 . (1.29)
. (1.29)
Для однородно-анизотропной среды, где  и
и  - проницаемости по горизонтали и вертикали пласта соответственно, требуется решить уравнение фильтрации [28]:
- проницаемости по горизонтали и вертикали пласта соответственно, требуется решить уравнение фильтрации [28]:
 . (1.30)
. (1.30)
Введем новую переменную и характеристику анизотропии  :
:
 ,
,  . (1.31)
. (1.31)
Тогда уравнение (1.30) переходит в обычное уравнение Лапласа для изотропной среды с координатами  :
:
 . (1.32)
. (1.32)
Пласт в новых координатах  , где вертикальные размеры действительного анизотропного пласта изменены в
, где вертикальные размеры действительного анизотропного пласта изменены в  раз, назовем приведенным однородным пластом.
раз, назовем приведенным однородным пластом.
Сравним дебит (на единицу ширины потока)  скважины в однородно-анизотропном пласте с дебитом
скважины в однородно-анизотропном пласте с дебитом  скважины приведенного пласта [28]:
скважины приведенного пласта [28]:
 . (1.33)
. (1.33)
Таким образом, решив задачу для приведенного изотропного пласта, воспользуемся старыми координатами, чтобы получить решение для однородно-анизотропного пласта. Нетрудно видеть, что уравнению (1.32) удовлетворяет решение, аналогичное решению (1.28), которое с учетом (1.29) и (1.30) при  записывается в безразмерном виде:
записывается в безразмерном виде:
 , (1.34)
, (1.34)
 ;
;  ;
;  . (1.35)
. (1.35)
Если принять за горизонтальную скважину линию стоков с плотностью расхода  на ширину потока по длине горизонтального ствола
на ширину потока по длине горизонтального ствола  , тогда дебит скважины
, тогда дебит скважины  , а уравнение (1.34) при переходе от потенциала
, а уравнение (1.34) при переходе от потенциала  к давлению
к давлению  при
при  представится в виде:
представится в виде:
 , (1.36)
, (1.36)
где
 . (1.37)
. (1.37)
Заметим, уравнение (1.34) может быть использовано для расчета предельных безводных (безгазовых) дебитов и депрессий в соответствии с теорией статического конусообразования Маскета-Чарного.
|
|
|


