Анализ методов оценки эффективности работы горизонтальных и наклонных скважин

 

Современным направлением формирования оптимальной системы разработки и повышения производительности малодебитных скважин сложнопостроенных залежей на поздней стадии разработки нефтяных месторождений является строительство пологих, горизонтальных и разветвленных скважин. Большое влияние на получаемый результат оказывает эффективность проектирования профиля, которая обеспечивает дальнейшую эксплуатационную надежность добывающих скважин. Согласование проектной траектории ствола скважин с естественными особенностями геологического строения в интервале продуктивного коллектора, в частности, с анизотропией пласта по проницаемости, может существенным образом расширить возможности регулирования процессов извлечения нефти. Очевидна высокая технологическая эффективность оптимизации траектории стволов скважин в нефтеносных зонах месторождений, для которых характерны достаточно большая послойная и зональная неоднородность коллекторов по проницаемости и наличии глинистых пропластков. Для выбора наилучшего технического решения необходимо надежное обоснование вскрытия продуктивной зоны наклонными и горизонтальными стволами.

На продуктивность скважин любого профиля в значительной степени оказывает влияние анизотропия пласта. Коэффициент продуктивности совершенных по степени и характеру вскрытия вертикальных скважин определяется по известной формуле:

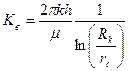, (2.1)

где - проницаемость, толщина пласта и коэффициент вязкости нефти, - радиус контура питания, 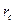- радиус скважины.

Если исходить из предположения, что анизотропия пласта равна 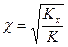, причем проницаемость по горизонтали неизменна во всех точках пласта по вертикали, то из формулы следует, что коэффициент продуктивности не зависит от анизотропии. Однако реальные пласты часто состоят из чередующихся проницаемых, непроницаемых и слабопроницаемых пропластков. Поэтому если пласт состоит из двух проницаемых пропластков толщиной и 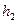(пропластки работают с одной депрессией) при общей толщине пласта 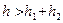, то коэффициент продуктивности определится следующим образом:

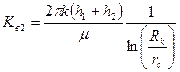. (2.2)

Из этого следует, что коэффициент продуктивности совершенных вертикальных скважин зависит от анизотропии пласта, если считать, что увеличение анизотропии пласта заключается в увеличении суммарной толщины непроницаемых пропластков.

Коэффициент продуктивности совершенной по степени вскрытия пласта наклонной скважины определяется по формуле:

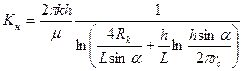, (2.3)

где - зенитный угол ствола скважины в интервале продуктивного пласта, - длина горизонтального ствола.

Коэффициент продуктивности горизонтальных скважин определяется по формуле:

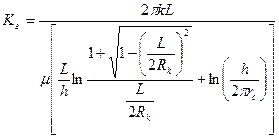. (2.4)

Очевидно, что коэффициенты продуктивности наклонных и горизонтальных скважин также зависят от анизотропии.

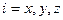В одной из работ М. Маскет предложил способ перехода от изотропного пласта к анизотропному путем умножения линейных размеров системы пласт-скважина по осям на величину , где , а 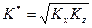- эквивалентная проницаемость пласта [28].

Это обеспечивает возможность найти отношение коэффициентов продуктивности для анизотропного пласта, подставив в формулы (2.1) и (2.4) соответствующие значения эквивалентных величин.

Для вертикальной скважины коэффициент продуктивности равен:

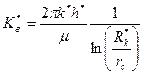, (2.5)

для горизонтальной:

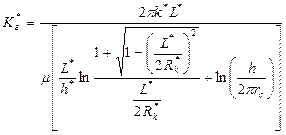, (2.6)

где ; ; .

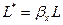Для получения аналогичной зависимости для наклонной скважины следует учитывать угол ее наклона. Проекция наклонной скважины на горизонталь 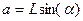изменится и станет равной 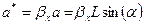. Вертикальная проекция, равная толщине пласта, станет равной . Таким образом, угол наклона станет равным 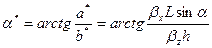. Длина наклонного ствола . Тогда коэффициент продуктивности наклонной скважины определяется по формуле

. (2.7)

Теперь можно построить зависимость отношения коэффициентов продуктивности горизонтальной, наклонной и вертикальной скважин от анизотропии, толщины пласта, зенитного угла и длины горизонтального ствола скважины.

 

Эффективность работы. Ряд авторов предложили уравнения для расчета коэффициента продуктивности горизонтальных скважин в однофазных системах. Наиболее широкое приложение нашли уравнения, полученные Джайджером, Джоши, Бейбу и Оде, Гудом и Кучуком. Все они рассмотрели поведение горизонтальной скважины в пределах замкнутой площади дренирования, принимая ряд упрощающих допущений [28, 102].

Уравнение Джоши получено как развитие формулы Джайджера. Уравнение Бейбу и Оде соответствует наиболее общему случаю и пригодно для большинства встречающихся ситуаций. Уравнение Джоши дается в самом простом виде и таким образом пригодно для ручных вычислений.

Уравнение Джоши для коэффициента продуктивности записано в виде:

, (2.8)

где ;

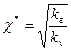. (2.9)

 

Основные ограничения состоят в том, что это уравнение справедливо только при и 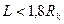и применимо только при стационарном режиме фильтрации.

В вышеприведенной формуле, а также в последующих формулах этого пункта приняты следующие условные обозначения: - половина большой оси эллипса дренирования, м; - пластовый объемный фактор нефти, м³ (в пластовых условиях)/м³ (в стандартных условиях); - геометрический фактор (в уравнении Бейбу – Оде, безразмерный); 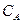- фактор формы для площади, дренируемой скважиной, безразмерный; 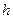- толщина пласта, м; 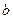- длина перфорированного интервала, м; - проницаемость, мкм², 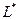- длина дренируемого пласта, м; - длина горизонтального ствола скважины, м; 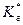- коэффициент продуктивности, м³/(сут·Па) в стандартных условиях; 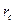- радиус скважины, м; - скин-эффект; - 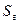скин-эффект для приствольной зоны горизонтальной скважины; - скин-эффект для приствольной зоны вертикальной скважины; 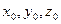- координаты от центра горизонтальной скважины; 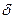- расстояние по вертикали от горизонтального ствола до средне точки продуктивного пласта, м; 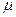- вязкость, мПа·с; - проницаемость в плоскости напластования; 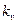- проницаемость, направленная перпендикулярно к плоскости напластования; - коэффициент, учитывающий загрязнение пласта; 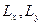линейные размер по осям и .

Уравнение Бейбу и Оде для горизонтальной скважины в направлении оси имеет вид:

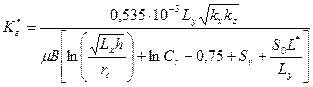. (2.10)

Параметры и зависят от площади дренирования и проницаемости. Это уравнение допускает псевдостационарные условия с отсутствием течения на границе; его более сложно применять для выполнения оценок, но оно может быть легко запрограммировано для осуществления расчетов на компьютере. Достоинство уравнения Бейбу и Оде состоит в том, что в нем используются разные значения проницаемости - и . Приведенное уравнение получено для горизонтальной скважины в направлении . Это уравнение свидетельствует о целесообразности бурения скважин перпендикулярно к направлению, в котором проявляется более высокая проницаемость. Согласно уравнению Бейбу и Оде горизонтальная скважина может пересечь всю площадь дренирования и, следовательно, ему неприсущи ограничения, характерные для уравнения Джоши. Однако существуют определенные ограничения в использовании уравнения Бейбу и Оде.

Наряду с уравнением, для которого справедливо отсутствие течения на границах, Гуд и Кучук получили уравнение для оценки коэффициента продуктивности горизонтальной скважины в бесконечной по площади системе с постоянным давлением на кровле и подошве продуктивного пласта, что соответствует условиям на границе с газовой шапкой и крупным водоносным горизонтом. Это уравнение представлено в следующем виде [28]:

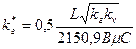, (2.11)

где

. (2.12)

Аналитические уравнения можно легко применять, чтобы продемонстрировать влияние различных параметров на продуктивность скважины.

 

Продуктивность пласта. В практике эксплуатации горизонтальных скважин существует несколько выражений для подсчета дебита. Рассмотрим основные, наиболее применяемые формулы:

по Джайджеру

 

; (2.13)

по Ренарду и Дюпюи

; (2.14)

 

 

по Джоши

, (2.15)

где 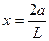- для эллипсоидной площади дренажа;

- половина большой оси эллипса.

В приведенных выражениях:

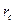- радиус скважины;

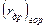- радиус области дренирования для горизонтальной скважины;

- вязкость нефти;

- объемный коэффициент нефти;

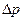- депрессия между границей области дренирования и забоем скважины.

 

Влияние анизотропии пласта на продуктивность пласта. Для пласта с различными горизонтальной и вертикальной проницаемостями уравнение Лапласа, которое описывает установившийся режим фильтрации притока, имеет вид:

(2.16)

или

, (2.17)

где

.

Эффективная проницаемость пласта определяется по формуле:

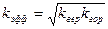. (2.18)

Влияние анизотропии пласта можно учесть, если представить толщину пласта как:

. (2.19)

Выражения, определяющие продуктивность, представляет собой решения для установившегося режима фильтрации и являются суммой двух слагаемых, один из которых описывает горизонтальный приток, а другой – вертикальный. Таким образом, влияние анизотропии пласта может быть учтено путем включения соответствующего параметра в член уравнения, описывающего вертикальный приток.

Подобная модификация выражения продуктивности по Джоши выглядит следующим образом [28]:

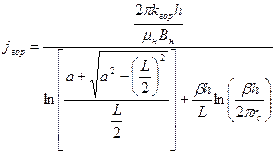, (2.20)

где .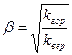

Модификация формулы Ренарда и Дюпюи, с учетом анизотропии пласта имеет вид:

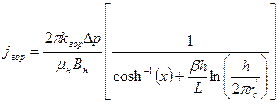, (2.21)

где .

Влияние расположения скважины на ее продуктивность. Тип пласта определяет допустимые глубинные отклонения при бурении горизонтальной скважины. Так, в пластах с непроницаемыми кровлей и подошвой (отсутствуют подошвенная вода и газ у кровли) идеальной является скважина, пробуренная по центру вертикального плана пласта. Как будет показано ниже, отклонение от центра снижает продуктивность скважины, причем тем меньше, чем длиннее ствол.

В пластах, для которых характерны явления конусообразования газа и воды, выбор места расположения скважины в вертикальном плане пласта очень важен. Поэтому, если с одной стороны отклонение горизонтальных скважин с большой длиной ствола от центра пласта незначительно снижает продуктивность, то с другой – является определяющим во времени прорыва в скважину газа и воды и соответственно в изменении газового и водонефтяного факторов. Таким образом, расположение скважины влияет на конечную величину запасов, извлекаемых конкретной горизонтальной скважиной.

При сравнении коэффициентов продуктивностей для горизонтальных скважин, пробуренных с отклонением от центра и по центру 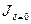для различного эксцентриситета 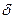, можно заметить, что если горизонтальная скважина имеет значительную длину по сравнению с толщиной пласта, то скважина может располагаться в любом месте вертикального плана без значительных потерь продуктивности. В общем случае показатели эксплуатации горизонтальной скважины не сильно зависят от эксцентриситета, если скважина отклонена от центра на 25% толщины пласта. Строго говоря, это верно для пластов, в которых отсутствуют подошвенная вода и газ удовлетворительно кровли.

Определение коэффициента продуктивности наклонно направленной скважины производится по формулам Кинко, Миллера и Рамэ. По ним же подсчитан скин-фактор для данных скважин и показано, что он зависит только от геометрии скважины [28].

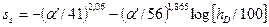(2.22)

для 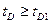и .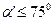

В представленной формуле:

; (2.23)

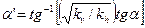; (2.24)

; (2.25)

; (2.26)

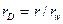(2.27)

где - угол наклона ствола скважины, 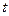– измеряется в часах

Выражение для эффективного радиуса ствола скважины:

(2.28)

и индекс продуктивности наклонной скважины может быть сравнен с индексом продуктивности вертикальной скважины без стимуляции с помощью уравнения:

. (2.29)

Van der Vlis и другие также представили формулу для расчета продуктивности наклонной скважины. Их формула, относительно эффективного радиуса ствола скважины, имеет следующий вид:

, (2.30)

где .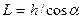

Обратите внимание, что уравнение получено путем замены 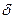на 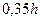и оно верно только для углов . Как отмечено ранее, уравнение может использоваться для расчета индекса продуктивности. Результаты расчета эффективного радиуса ствола скважины и скин-фактора, произведенные с помощью уравнений Van der Vlis, Cinco и других, уравнения очень близки. Поэтому любое из перечисленных уравнений может использоваться для расчетов.

Как было отмечено ранее, использование горизонтальных скважин эффективно в пластах небольшой толщины, в то время как наклонно направленные скважины высокоэффективны в пластах большой толщины. В связи с этим важно найти оптимальное решение при выборе профиля забоя в процессе заканчивания скважины в пласте данной толщины. Одним из путей является предположение, что бурящаяся скважина имеет фиксированную длину забоя, ствол которого может быть вертикальным, горизонтальным или наклонно направленным. Сравнение продуктивностей скважин при разных стволах забоя позволяет определить оптимальный вариант заканчивания скважины.

Горизонтальная скважина имеет значительное преимущество по сравнению с наклонно направленной в пласте толщиной 30 м, даже при низких значениях . Для пласта толщиной 120 м коэффициент продуктивности горизонтальной скважины выше соответствующей наклонно направленной для однородного пласта 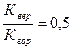. Однако, если вертикальная проницаемость составляет 1/10 горизонтальной, то показатели эксплуатации наклонно направленной скважины лучше, чем горизонтальной. Это указывает на то, что в пластах большой толщины использование горизонтальных скважин может быть эффективным, если вскрыты пласты высокой проницаемости в вертикальном направлении. С другой стороны, это указывает на то, что в пластах большой толщины и низкой вертикальной проницаемости может быть необходимо применение методов воздействия на призабойную зону для повышения экономичности предлагаемого проекта разработки месторождения горизонтальными скважинами.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: