 |
Математические модели притока к наклонным скважинам
|
|
|
|
Модели притока к наклонным скважинам в неограниченном пространстве и полупространстве. Первые уравнения притока флюида к наклонной скважине были получены также Полубариновой-Кочиной для неограниченного и полуограниченного пространства с использованием известного решение уравнения Лапласа для линии равных стоков
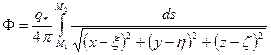, (1.40)
где 
- начальная и конечная точка оси горизонтального ствола, 
- длина дуги от точки 
вдоль 
, 
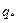- отнесенный к длине наклонного ствола массовый расход (дебит) скважины,
, 
, 
, 
, 
, 
, 
.
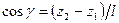С учетом этих соотношений впервые был получено аналитическое выражение для потенциала поля скоростей в случае притока флюида к наклонной скважине в безграничном пространстве.
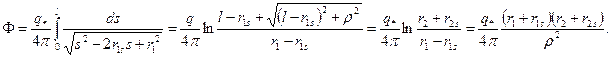
В работе [16] приведено также решение задачи о притоке флюида к наклонной скважине в полупространстве. Как и прежде считаем, что наклонный ствол скважины, концы которого имеют координаты 
, равномерно нагружен стоками интенсивностью 
. Для того чтобы обеспечить непроницаемость верхней границы полупространства отрезок 
отразим относительно плоскости 
и получим отрезок нагрузить равномерными стоками интенсивностью , то искомое решение можно представить в виде суммы решений для обоих отрезков.
, (1.41)
где 
- длина наклонного ствола,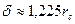 
, 
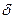- эквивалентный радиус наклонного ствола, 
определяется по формуле
. (1.42)
Если отрезок вращать вокруг середины 
, сохраняя его длину, то
, (1.43)
где 
.
Для системы наклонных скважин решение задачи получается путем сложения потенциалов, создаваемых отдельными стволами, т.е. линейными стоками. При этом считается, что эквивалентные поверхности, охватывающие отрезки, нагруженные стоками, на достаточно малых расстояниях от них будут близки к экспоненциальным. На этом основании система действенных скважин заменяется системой эквивалентных поверхностей, охватывающих линейные стоки. Потенциалы скорости фильтрации, создаваемые этими поверхностями складываются.
|
|
|
В работе [15] рассмотрен также случай наклонных скважин одинаковой длины, расположенных в полупространстве по поверхности конуса, ось которого совпадает с осью 
. При этом одна скважина помещена в плоскости 
, а другие – в плоскостях, составляющих соответственно углы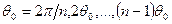 
с плоскостью . Для решения задачи используются цилиндрические координаты: 
. Уравнение для дебита каждой из скважин, т.е. уравнение притока к скважине, получено в следующем виде
, (1.44)
где 
- массовый дебит и длина наклонного ствола, 
, 
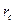- радиус наклонного ствола, 
- значение потенциала на контуре питания, т.е. на бесконечном удалении ствола.
Математические модели притока к наклонным скважинам в пласте конечной толщины. Наиболее простая модель притока однофазного флюида к наклонной скважине в пласте конечной длины была предложена Борисовым Ю.П. в следующем виде [2]:
, (1.45)
где 
- массовый дебит наклонной скважины, 
- дебит наклонной газовой скважины и плотность газа, приведенные к стандартным условиям, - длина наклонного ствола, 
- проницаемость породы,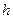 
- толщина пласта, 
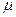- динамическая вязкость газа, 
- радиус ствола и контура питания, соответственно, 
- угол наклона ствола вертикали, 
- псевдодавление, 
- плотность газа в пластовых условиях, 
, 
- давление газа в пластовых условиях, 
- коэффициент сжимаемости газа, 
- газовая постоянная, 
- пластовая температура, 
- псевдодепрессия, 
- значение функции на контуре питания пласта и стенке наклонного ствола скважины, соответственно, в стандартных условиях 
.
В случае идеального газа уравнение (1.45) примет вид:
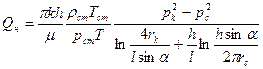. (1.46)
В уравнениях (1.45) и (1.46) входит величина радиуса контура питания, который невозможно измерить непосредственно, но который остается постоянным или слабо меняется в процессе разработки. Для определения этого параметра используем уравнение притока газа к наклонной скважине
|
|
|
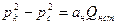, (1.47)
где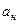 
- коэффициент линейного фильтрационного сопротивления, определяемый после обработки результатов гидродинамических исследований на стационарных режимах фильтрации.
Уравнение (1.46) с учетом (1.47) можно представить в следующем виде
. (1.48)
Из этого уравнения находим, что
, 
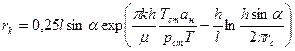(1.49)
Здесь неизвестным является параметр 
, который можно определить по имеющимся картам проводимости пласта и его толщины. Уравнение (1.49) позволяет найти некоторый условный радиус контура питания, с помощью которого можно определить реальные фильтрационные параметры пласта и скважины.
При проектировании разработки месторождения системой наклонных скважин необходимо оценить эффективность из применения по сравнению с вертикальными скважинами. В то же время в период разведки первоначально бурят только вертикальные скважины и при расчетах продуктивности наклонных скважин приходится пользоваться данными, полученными при гидродинамических исследованиях вертикальных скважин, дебиты которых определяются по формуле:
. (1.50)
Пусть первоначально известны результаты гидродинамических исследований вертикальной скважины, из которых находим проводимость пласта 
. Дебит наклонной скважины, пробуренной в той же точке, определяется по формуле
, (1.51)
где 
- параметры скважины №1.
Для оценки гидродинамической эффективности применения наклонной скважины 
вводят понятие обобщенного индекса продуктивности скважины, определяемого по формуле
. (1.52)
Для вертикальной скважины 
; для наклонного ствола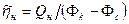 
, коэффициент гидродинамической эффективности определяется отношением 
при одной и той же обобщенной псевдодепрессии 
.
|
|
|
