Метод построения кривой восстановления давления и их обработка

Результирующая величина D P в формуле в течение непродолжительного времени t определяется главным образом вторым слагаемым, определяемым по формуле:

,

где р _с – текущее давление на забое скважины после остановки, атм;

r _с – радиус скважины.

То есть можно записать:

,

где за р _заб принимается давление на забое перед остановкой скважины.

Поэтому при анализе кривой восстановления можно пользоваться следующей формулой:

.

Обозначив: ; ,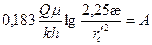

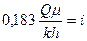где А – отрезок на оси D Р, отсекаемый прямолинейным участком кривой восстановления в координатах D Р и lg t;

i – угловой коэффициент наклона прямолинейного участка к оси lg t.

Можно выразить æ по формуле:

.

Если при построении кривой восстановления в координатах D Р и lg t начало координат перенесено или графически трудно отыскать отрезок A, то вместо выше приведенной формулы можно использовать следующую:

.

Обработка кривых восстановления давления (КВД). В основу упрощенного метода обработки кривых восстановления давления положено приближенное уравнение притока:

,

которое при 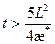допускает логарифмическую аппроксимацию:

,

где С _г вычисляется по формулам (1.2).

Алгоритм обработки КВД по упрощенному методу. Первоначально производится проверка условия 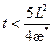или .

Если 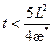, то по данным исследования скважин строят график КВД в координатах 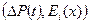, где . По углу наклона асимптоты i вычисляется гидропроводность пласта 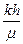, а по точке пересечения асимптоты с осью абсцисс вычисляется С _г.

Если , то график КВД строится в координатах . При этом гидродинамические параметры 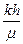и С _г вычисляются аналогично вертикальным скважинам.

Уточненный метод Бадри. Данный метод предусматривает идентификацию режимов течения по форме графика КВД в координатах 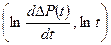, обеспечивающие возможность предварительного определения гидродинамических параметров, характеризующих свойства продуктивного пласта.

Анализ процессов идентификации режимов течения и оценка пара­метров пласта требует необходимости определения профиля притока в скважину. Время начала и конца каждого режима течения зависит от про­ницаемости К _ги анизотропии æ^* пласта, эффективной длины горизонталь­ного ствола L _эф и расстояний до кровли и подошвы пласта Z ₀.

Согласно методу Бадри, представленному в работе [101], модель скважины с горизонтальным стволом и соответствующие режимы течения включают первый, второй и третий пе­риоды радиального течения, а также промежуточные периоды линейных течений (рис. 1.4 и 1.5).

Алгоритм обработки КВД по уточненному методу Бадри. Первый период радиального течения идентифицируется по первому горизонтальному участку кривой 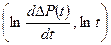(рис 1.4). Определив угловой коэффициент i для прямолинейного участка кривой (рис 1.5), рассчитывается гидропроводность пласта:

, (1.18)

где К_у и K_z – проницаемости по осям Y и Z соответственно, мкм²;

L _эф– эффективная (работающая) длина горизонтального ствола, м;

q _г– дебит скважины перед закрытием на исследования, м³/сут;

m– вязкость нефти, мПа×с.

Второй период радиального течения наступает после окон­чания влияния кровли или подошвы пласта и может быть идентифицирован по второму горизонтальному участку кривой (рис. 1.4). Угловой коэф­фициент i соответствующего прямолинейного участка кривой (рис. 1.5) в 2 раза больше первого радиального течения. Тогда формула (1.18) запи­шется в виде:

. (1.19)

Если длина горизонтального ствола намного превосходит толщину пласта (L>>h), то после окончания эффектов, связанных с кровлей и по­дошвой пласта, может наступить промежуточный период линейного течения (рис. 1.4). Этот период идентифицируется прямой с угловым коэффициентом i = 0,5. В этом случае применяется формула следующего вида:

.

После второго линейного режима течения в плоскости горизонталь­ного ствола развивается третий период радиального течения (рис 1.4). На графике в полулогарифмическом масштабе (рис 1.5) соответст­вующая прямая линия имеет угловой коэффициент i. Тогда гидропроводность пласта рассчитывается по следующей формуле:

.

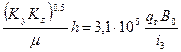Идентификация режимов течения необходима для предварительной оценки параметров продуктивного пласта, которые впоследствии уточня­ются при сравнениях фактических данных с расчетными.

Если расстояние Z ₀ от горизонтального ствола до границы пласта из­вестно, то можно определить проницаемость по напластованию и перпендикулярное ему К_z. Формулы (1.18) и (1.19) позволяют опреде­лить параметр . Определив по формулам (1.5) и (1.7) верти­кальные проницаемости К_z и принимая при известной длине гори­зонтального ствола, по формулам (1.4) и (1.6) можно определить про­ницаемость вдоль напластования.

Принимая 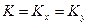, из формулы (1.9) можно определить про­ницаемость в плоскости напластования, затем из формул (1.8) и (1.4) нетрудно определить эффективную длину горизонтального ствола .

 

⇐ Предыдущая21222324252627282930Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: