Анализ режимов притока к горизонтальному стволу

В общем комплексе гидродинамических исследований скважин ме­тод восстановления давления нашел широкое применение. Анализы кривых восстановления давления (КВД) при неустановившейся фильтрации жидко­сти в пласте, которые уже давно применяются при гидродинамических ис­следованиях вертикальных скважин, позволяют раздельно оценить пара­метры призабойной и удаленной зон пласта, неоднородность пласта по про­ницаемости и выявить литологические экраны. Кроме задач, связанных с изучением коллекторских свойств пласта и его строения, этот метод широко используется в решении задач контроля процессов разработки. Немалое значение приобретает метод при оценке эффективности воздействия на призабойную зону скважины и на весь продуктивный пласт.

При интерпретации КВД в горизонтальных скважинах особо важным является объяснение и оценка факторов, определяющих форму КВД. К ним относятся как технологические факторы (приток жидкости в скважину по­сле ее остановки, нарушение режима работы скважины перед исследовани­ем), так и факторы, связанные с неоднородностью пласта, скин-эффектом, с влиянием границ пласта и последовательным развитием различных режи­мов течения после закрытия скважины, детальный анализ режимов течения произведен в работах [101, 99, 87].

Факторы, определяющие форму КВД:

На форму кривых вос­становления давления особое влияние оказывают границы пласта, наруше­ние геометрии потока в призабойной зоне, приток жидкости в скважину после ее остановки, нарушение режима работы скважины перед ее останов­кой, профиль притока и др. Перечисленные факторы искажают КВД и за­трудняют их интерпретацию. Однако при успешной интерпретации таких кривых появляется возможность оценки: неоднородности пласта и типа коллектора, последовательности перехода одного режима течения в другой, неньютоновских свойств жидкости, емкостных характеристик пористого и трещиновато-пористого пластов в процессе разработки и др.

Обычно принимаемая модель бесконечного пласта не соответствует действительности. Реальные пласты имеют конечные размеры. Но посколь­ку продолжительность обычных гидродинамических исследований невели­ка, то за время таких исследований границы пласта по протяженности или совсем не оказывают влияния на форму КВД или это влияние практически не ощутимо. Поэтому схема бесконечного пласта при обычных гидродина­мических исследованиях скважин практически вполне приемлема. Однако кровля, подошва продуктивного пласта, а также сбросы, находящиеся вблизи горизонтальной скважины, будут существенно влиять на развитие режи­мов течения, их продолжительности и, в конечном счете, на форму КВД.

Неоднородность пласта обычно характеризуется по изменениям коллекторских свойств пласта и физических свойств насыщающих его жидко­стей. В периоды гидродинамических исследований скважин можно считать параметры пласта (гидропроводность и пьезопроводность æ) в каждой точке неизменными. Это допущение позволяет путем сопоставления КВД, снятых в разные периоды времени, судить о характере вытеснения.

Многочисленными теоретическими и экспериментальными исследо­ваниями показано влияние гидродинамического несовершенства вертикаль­ных скважин и скин-эффекта призабойной зоны на характер КВД. Для гори­зонтальных скважин указанные факторы, а также профиль притока (эффек­тивно работающая часть фильтра горизонтальной скважины) сказываются в наибольшей степени. Поэтому в уравнение, описывающее кривую восста­новления давления, необходимо ввести добавочные фильтрационные со­противления, обусловленные несовершенством скважины, скин-эффектом и анизотропией пласта, или приведенный радиус скважины.

Существенными факторами, влияющими на форму КВД, являются нарушение стационарного режима фильтрации перед исследованием и на­личие притока жидкости в скважину после ее остановки. Указанные факто­ры можно назвать технологическими, которые могут быть исключены при изменении технологии исследования. Например, если снимать КВД при закрытии скважины на забое, то нет необходимости учета притока жидко­сти в скважину. При вскрытии продуктивного пласта горизонтальным ство­лом увеличивается коэффициент продуктивности, что сокращает продолжи­тельность притока в скважину при закрытии ее на устье. Поэтому можно ограничиться рассмотрением обработки КВД без учета притока.

Нарушение режима работы скважины перед ее остановкой и особен­ности интерпретации КВД в этих случаях подробно рассмотрены в работе [56].

Упрощенный метод обработки КВД в скважинах с горизон­тальным стволом (бесконечный пласт). Рассматривается бесконечный по простиранию одно­родно-анизотропный горизонтальный пласт постоянной толщины h, насы­щенный однородной жидкостью, дренирующий скважиной с горизонталь­ным стволом длиной L, произвольно расположенным относительно непро­ницаемых кровли и подошвы.

Предлагается обрабатывать аналогично кривым для вертикальных скважин, используя приближенное уравнение притока:

(1.1)

при

(1.2)

где q - дебит скважины в момент остановки;

k - проницаемость пласта по горизонтали;

К_{z -} проницаемость пласта по вертикали;

h - толщина продуктивного пласта;

æ - коэффициент пьезопроводности;

t - время восстановления давления;

r _с - радиус скважины;

С _r - добавочные фильтрационные сопротивления, обусловленные гео­метрическими параметрами и анизотропией (геометрический псевдоскин-эффект);

L - длина горизонтального ствола скважины;

æ^* - коэффициент анизотропии пласта;

m - коэффициент вязкости жидкости.

Формулой (1.2) можно с достаточной точностью пользоваться при любом расположении горизонтального ствола относительно кровли и по­дошвы. При симметричном расположении скважины в формуле (1.2) сле­дует вместо 4p принять значение 2p.

Продолжительность остановки, после которой КВД можно обрабаты­вать без учета притока, можно оценить по формуле, вытекающей из выра­жения для наклонной скважины [99]:

(1.3)

где коэффициент емкости ствола, когда он полностью заполнен жидкостью, определяется из выражения:

,

здесь V – объем ствола скважины;

b_æ - коэффициент сжимаемости жидкости.

Если ствол заполнен жидкостью не полностью, то коэффициент емкости можно определить из выражения:

,

где V_n – объем ствола на 1 метр длины, м³;

r - плотность жидкости, кг/м³.

Скин-эффект S в формуле (1.3) может быть быть определен известными методами. Новый эффективный метод определения S предложен в работе Кутасова [15].

При подсчете продолжительности исследования скважины в формуле (1.3) принимаются следующие размерности:

[ V ]=м³; [ b _æ]=Па^-1; [ h ]=м; [ r_c ]=м; [ k ]=м²; [m]=Па×с, [ t ]=c.

Стоит отметить, что в уравнении притока (1.1) не учитываются: добавочные фильтрационные сопротивления С₀, обусловленные перфорацией горизонтального ствола; скин-эффект S, обусловленный изменением проницаемости призабойной зоны; эффективная длина горизонтального ствола, дренирующего продуктивный пласт, обусловленная профилем притока; режимы течений (радиальный, линейный, сферический, двухлинейный), имеющие место при гидродинамических исследованиях горизонтальных скважин, их последовательный переход из одного вида в другой и продолжительность [101, 99, 87].

Уточненный метод Бадри гидродинамических исследований горизонтальных скважин и интерпретации КВД. Методика интерпретации данных исследований при анализе КВД в скважинах с горизонтальным стволом такая же, как и в вертикальных, поскольку в обоих случаях идентифицируются режимы течения, которые обеспечивают возможность предварительного определения гидродинамических параметров, характеризующих свойства продуктивного пласта. Предварительные оценки затем уточняются с использованием программы для решения обратных задач [27].

Анализ процессов идентификации режимов течения и оценки параметров пласта требует необходимости определения профиля притока в скважину.

Пласт бесконечный, однородно-анизотропный с непроницаемыми кровлей и подошвой, дренируемый горизонтальной скважиной. Кривая восстановления давления описывается обобщенным уравнением пьезопроводности для горизонтальной скважины. По результатам исследования согласно [101] строятся кривые зависимости в логарифмическом масштабе:

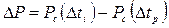
и производная изменения:

где t - время, обусловленное суперпозицией потоков до и после остановки скважины;

,

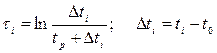где P _c(Dt_i) – восстановленное забойное давление после закрытия скважины;

t_p – время работы скважины до ее закрытия;

P _c(t_p) – давление на забое скважины перед ее остановкой;

t_i – время восстановления давления на забое;

i – интервал отсчета.

Применительно к скважинам с горизонтальным стволом время начала и конца каждого режима течения зависит от проницаемости и анизотропии пласта, скин-эффекта, эффективной длины горизонтального ствола и расстояний до границы пласта (кровли или подошвы). Согласно методу Бадри, изложенному в работе [27], модель скважины с горизонтальным стволом и соответствующие режимы течения включают первый, второй и третий периоды радиального течения, а также промежуточные периоды линейных течений (рис. 1.4).

Первый период радиального течения идентифицируется по первому горизонтальному участку кривой производной в логарифмическом масштабе. Определив угловой коэффициент n для прямолинейного участка кривой в полулогарифмическом масштабе (рис. 1.5), параметр произведения К (проницаемости) и L (длины ствола) можно рассчитать по формуле [27]:

, (1.4)

где K_y и K_z – проницаемость по оси Y и перпендикулярно ей по оси Z соответственно, мкм²;

L_эф – эффективная (работающая) длина горизонтального ствола, м;

q – дебит скважины перед закрытием ее на исследование, м³/сут;

m – вязкость нефти, мПа×с.

Конец периода радиального течения соответствует моменту, когда начинает проявляться влияние ближайшей границы пласта. Время, необхо­димое для проявления этого эффекта, зависит от проницаемости по вертикали K_z и расстояния Z₀ от горизонтального ствола до ближайшей границы пласта. Если расстояние Z₀, известно, то проницаемость К_z можно оценить по времени t, когда кривая в логарифмическом масштабе начинает отклонятся от горизонтального участка, соответствующего радиальному режиму течения (рис. 1.4):

(1.5)

где m – коэффициент пористости, %;

b^* – коэффициент упругоемкости пласта, Па^-1;

t ₀₁ – время начала отклонения производной давления по времени от

горизонтального участка, час;

Z ₀ – расстояние от горизонтального ствола до ближайшей непроницае­мой границы (кровли или подошвы), м;

h – толщина продуктивного пласта, м;

K_z – вертикальная проницаемость, мкм².

 

 

Рис. 1.4. Зависимость производной изменения забойного давления по времени от време­ни восстановления давления после закрытия скважины в билогарифмическом масштабе (схема полной типовой КВД в горизонтальной скважине, дренирующей бесконечный пласт при фильтрации однородной жидкости):

1 — влияние емкости ствола скважины; 2 — первый период радиального течения; 3 — пере­ходный период от радиального к линейному режиму течения; 4 — первый период линейного течения; 5 — переходный период от первого линейного ко второму радиальному режиму тече­ния; 6 — второй период радиального течения; 7 — переходный период от второго радиального ко второму линейному режиму течения; 8 — второй период линейного режима течения; 9— переходный период от второго линейного к третьему радиальному режиму течения; 10 — третий период режима радиального течения

 

Рис. 1.5. Зависимость производной изменения забойного давления по времени от време­ни восстановления давления после закрытия скважины в полулогарифмическом масштабе (схема полной КВД в горизонтальной скважине):

1 — влияние емкости ствола скважины; 2, 6, 10 — периоды радиального течения; 3, 5, 7, 9 — переходные периоды от радиальных к линейным режимам течения; 4, 8 — первый и второй периоды линейного режима течения

 

 

Второй период радиального течения наступает после окончания влияния ближайшей непроницаемой границы пласта (кровли или подошвы) и может быть идентифицирован по второму горизонтальному участку кри­вой (рис. 1.4). Угловой коэффициент соответствующего прямолиней­ного участка кривой (рис. 1.5) в 2 раза больше, чем для первого ради­ального течения. Тогда формула (1.4) запишется в виде:

. (1.6)

Влияние дальней непроницаемой границы пласта соответствует кон­цу второго периода радиального течения (рис. 1.4). Если в этом случае известно расстояние Z ₀, то для определения значения К_z применяется фор­мула [27]:

, (1.7)

где t ₀₂ – время начала отклонения кривой от горизонтального участка, со­ответствующего второму радиальному режиму течения (рис. 1.4).

Если длина горизонтального ствола намного превосходит толщину пласта (L >> h),то после окончания эффектов, связанных с кровлей и по­дошвой пласта, может наступить промежуточный период линейного тече­ния (обозначение 8 на рис. 1.4). Этот период идентифицируется прямой с угловым коэффициентом п = tg a= 0,5 (рис. 1.4). Тогда из построенной графи­ческой зависимости определяется [27]:

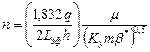. (1.8)

Если на любой границе продуктивного нефтенасыщенного пласта (случай, когда дренируется нефтяной пласт нефтегазовой залежи с подош­венной водой и верхним газом горизонтальной скважиной, а границами яв­ляются ВНК и ГНК) поддерживается постоянное давление, то этот период режима линейного течения отсутствует.

После второго линейного режима течения в плоскости горизонталь­ного ствола развивается третий период радиального течения (рис. 1.4). На графике в полулогарифмическом масштабе (рис. 1.5) соответст­вующая прямая линия имеет угловой коэффициент [27]:

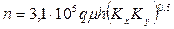. (1.9)

Идентификация режимов течения необходима для предварительной оценки параметров продуктивного пласта, которые впоследствии уточняют­ся при сравнении фактических данных с расчетными. Если расстояние Z ₀ от горизонтального ствола до границы пласта известно, то можно определить проницаемость по напластованию (K_xK_y)^0,5и перпендикулярно ему K_z.

Формулы (1.4) и (1.6) позволяют определить параметр . Оп­ределив по формулам (1.5) и (1.7) вертикальную проницаемость K_z при исходных параметрах т, m и b ^*, принимая при известной эффек­тивной длине горизонтального ствола по формулам (1.4) и (1.6), можно определить проницаемость вдоль напластования.

Принимая ,из формулы (1.9), можно определить про­ницаемость в плоскости напластования, затем из формулы (1.8) или (1.4) нетрудно определить эффективную длину горизонтального ствола скважины.

Скважина с постоянным давлением на границе пласта. Если на одной из непроницаемых границ пласта (ГНК или ВНК) поддержи­вается постоянное давление, то второй линейный и третий радиальный пе­риоды течений проявляться не будут. В этом случае оценить параметры продуктивного пласта можно только по первому и второму периодам ради­ального течений, используя формулы (1.4)-(1.7).

Если эффективная (рабочая) длина горизонтального ствола меньше действительной величины ствола (L _эф < L), то при использовании величины L в расчетах будут получаться заниженные значения .

Для скважин с горизонтальным стволом, характеризующихся посто­янным давлением на границе пласта, при оценке параметров коллектора требуется дополнительная информация об эффективной длине ствола. На­личие установок для принудительного спуска гибкой колонны насосно-компрессорных труб (НКТ) с проходящим внутри кабелем через герметизи­рованное устье делает возможным снятие профиля притока в горизонтальный ствол, что позволяет исключить из модели скважины переменный па­раметр L _эф и уменьшить риск некорректного определения параметров пла­ста.

Для скважины с горизонтальным стволом и двумя непроницаемыми границами продуктивного пласта (ГНК и ВНК) продолжительность време­ни, необходимая для достижения промежуточного периода радиального течения, много выше, чем время, требуемое для достижения радиального течения в вертикальной скважине. Этот факт должен учитываться при про­ведении исследования горизонтальной скважины. Установление величины L _эф из профиля притока повышает достоверность анализа результатов испы­тания скважины даже в том случае, если его продолжительность явно не­достаточна для достижения промежуточного периода радиального течения.

Установление режима течения. На построенных в логариф­мическом масштабе кривых перепада давления и его производной выделя­ется важный период времени, в котором кривая производной давления име­ет горизонтальный участок, свидетельствующий о радиальном режиме те­чения. При использовании модели, допускающей существование границы с постоянным давлением, этот участок интерпретируется как соответствую­щий второму периоду радиального течения. На графике, построенном по методу Хорнера, четко выделяется прямолинейный участок, причем влияние границы с постоянным давлением начинает проявляться приблизитель­но через 2 часа.

Параметры, полученные в результате интерпретации результатов ис­следования скважины, таковы:

радиус ствола, м	0,078
пористость, %	23,0
толщина пласта, м	12,5
приблизительно эффективная длина горизонтального ствола, м	50,0
расстояние до нижней границы пласта, м	8,3
пластовый объемный фактор нефти В 0,м3/м3	1,0
коэффициент вязкости нефти, мПа×с	8,0
общий коэффициент сжимаемости, кПа-1	2×10-6
объемная скорость притока, м3/сут:
D t = 0 час.	172,4
D t =9,61 час.

При использовании этих данных и D t = 2 час по уравнению (1.7) проницаемость, в направлении перпендикулярном к плоскости напластова­ния, была оценена в 0,007 мкм², то есть оказалась намного ниже, чем ожида­лась.

При значении эффективной длины горизонтального ствола, опреде­ленной на основании профиля притока в скважину, по уравнению (1.6) была оценена проницаемость в направлении, перпендикулярном к плоско­сти напластования, при этом предполагалось, что в горизонтальной плоско­сти пласт изотропен 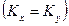. Оцененная проницаемость в плоскости на­пластования в 67,44 мкм² невозможна; следовательно, предположение о существовании второго периода радиального течения некорректно.

Совмещение данных восстановления давления с эталонными кривы­ми показало, что расчетное значение проницаемости в плоскости напласто­вания (1,295 мкм²) оказалось сравнительно близким ожидаемому значению (1,0 мкм²). Эффективная длина горизонтального ствола (67 м) хорошо со­гласуется с результатами, полученными при определении профиля притока в скважину. Тем не менее, проницаемость в направлении, перпендикулярном к плоскости напластования (0,0083 мкм²), оказалась гораздо ниже ожидав­шегося значения (0,5 мкм²).

Как свидетельствуют данные, полученные в соседних скважинах, продуктивный пласт характеризуется повышенной сланцеватостью у конца горизонтального ствола. Поскольку, согласно измеренному профилю при­тока в скважину, большая часть притока приходится на конечный участок горизонтального ствола, разумно ожидать, что расчетная эффективная про­ницаемость в направлении, перпендикулярном к плоскости напластования, гораздо ниже, чем в более высококачественном коллекторе. Без данных о распределении притока в скважину по длине ствола вообще невозможно расчетным путем оценить проницаемость пласта в направлении, перпенди­кулярном к плоскости напластования.

В попытке выявить причину, по которой не удалось идентифициро­вать режим течения с целью разумной оценки проницаемости в плоскости напластования, были подготовлены дополнительные эталонные кривые без учета эффектов, искажающих данные о давлении в малые периоды времени после закрытия скважины. Эталонная кривая производной давления, полу­ченная без учета притока в скважину и скин-эффекта, показывает, что гори­зонтальный участок на зарегистрированной кривой производной давления обусловлен не радиальным течением, а комбинацией притока в скважину и скин-эффекта. Таким образом, удалось объяснить, почему оценка прони­цаемости в плоскости напластования по уравнению (1.6) для радиального течения оказалась некорректной. Уравнения (1.4) и (1.6) справедливы только для радиального режима течения.

В заключение следует отметить, что при исследовании скважин с гори­зонтальным стволом достоверность анализов данных для неустановившего­ся режима повышается, если известны эффективная длина ствола и профиль притока в скважину. Подобная информация действительно необходима для предварительной оценки проницаемости в плоскости напластования путем идентификации режима течения в случае постоянства давления на границе пласта. Располагая такой информацией, мы можем селективно заканчивать и обрабатывать наиболее продуктивные интервалы в горизонтальном ство­ле, что позволяет поддерживать оптимальную производительность на про­тяжении всего срока эксплуатации скважины.

Идентификация режима течения в скважине с горизонтальным стволом, тем не менее, сопряжена со значительными трудностями. Начало и окончание периодов, соответствующих отдельным режимам течения, зави­сят не только от параметров коллектора (проницаемость, анизотропия, скин-эффект), но и от эффективной длины горизонтального ствола, а также от положения относительно верхней и нижней границ пласта. Неприемле­мые или нереальные оценки параметров, исходя из идентификации режима течения, свидетельствуют о том, что начальные допущения относительно режимов течения некорректны.

Как продемонстрировано на промысловом примере, совмещение фактических данных с эталонной кривой с использованием программ для решения обратных задач чрезвычайно важно при анализе результатов ис­следования скважин с горизонтальным стволом при неустановившемся ре­жиме. После получения решения возможность использования дополнитель­ных эталонных кривых, построенных без учета эффектов в начальные пе­риоды времени после закрытия скважины, может улучшить представления о режимах течения. Такие дополнительные эталонные кривые могут также объяснить разногласия в процессе интерпретации данных.

⇐ Предыдущая20212223242526272829Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: