Интерпретация результатов гидродинамических исследований горизонтальных скважин по методике В. С. Евченко

В основу обработки результатов гидродинамических исследований В.С. Евченко заложена приближенная формула:

,

где . (1.20)

Примечательным в приближенном выражении (1.20) является то, что величина коэффициента a определяется ис­ключительно геометрическими размерами. Это обстоятельство позволяет построить методы обработки данных гидропрослушивания в горизонталь­ных скважинах по аналогии с вертикальными.

Расчетные формулы для определения гидропроводности 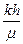и пьезопроводности æ с конкретизацией пометодам графической обработки данных гидропро­слушивания в горизонтальных скважинах имеют следующий вид:

Метод эталонных кривых.

, (1.21)

где D Р _ф и t _ф – координаты фактической кривой, соответствующие единичным координатам эталонной кривой.

Дифференциальный метод.

, (1.22)

где в – отрезок, отсекаемый на оси ординат .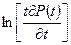

Интегральный метод. Если в является отрезком, отсекаемым на оси ординат 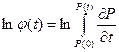, то используются формулы следующего вида:

. (1.23)

 

Если в является отрезком, отсекаемым на оси ординат , то используются формулы следующего вида:

, (1.24)

где t ₀ – некоторая положительная величина, имеющая размерность времени;

n – некоторое целое положительное число.

Приближенный метод. В данном методе используется формула (1.23) при условии, что в является отрезком, отсекающим на оси ординат .

В формулах (1.22)-(1.24) наклон преобразованного графика рассматривается относительно оси абсцисс .

Существуют расчетные зависимости для определения пьезопро­водности по характерным точкам кривой изменения давления в реагирую­щей скважине:

по точке перегиба: по точке «начала реагирования»:

; ;

 

по точке касания: по точке максимума:

; ,

где t _п, t _н, t _к, t _max – время, соответствующее последовательно точкам перегиба, начала реагирования, касания и максимума на графике ;

t ₀ – промежуток времен между моментами первого и второго измерений режима работы возмущающей скважины.

Все приведенные в этом пункте формулы для обработки результатов гидропрослуши­вания следует применять только тогда, когда одна из скважин, участвующих в исследовании, (возмущаю­щая или реагирующая) горизонтальная, а другая - вертикальная. В случае если возмущающая (длина а)и реагирующая (длины в) скважины горизон­тальны и, кроме того, параллельны, то при условиях, исследо­ванных выше, можно записать:

,

где 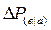– изменение давления в реагирующей горизонтальной скважине длины в, параллельной возмущающей горизонтальной скважине длины а;

x ₁ и x ₂ – абсциссы концов реагирующей горизонтальной скважины.

Если возмущающая и реагирующая горизонтальные скважин взаимно-перпендикулярны, то:

,

где – изменение давления в реагирующей горизонтальной скважине длины в, перпендикулярной возмущающей горизонтальной скважине длины а;

y ₁ и y ₂ – ординаты концов реагирующей горизонтальной скважины.

В соответствии с этими формулами при определении пара­метров пласта следует в расчетные зависимости (1.21)-(1.24) взамен множителей и aподставлять для параллельных возмущающей и реагирующей скважин и b, а для взаимно перпендикулярных - и g.

В связи с эксплуатацией горизон­тальных скважин актуальными для них являются также вопросы обработки кривых восстановления давления. Для того чтобы обработка кривых восстановления давления могла проводиться методами графической интерпретации, обычно применяемой в нефтепромысловой практике, пере­менная часть решения, зависящая от времени, должна быть представлена соответствующим образом.

Приближенное решение позволяет применять для определения пара­метров пласта известные методы графической обработки результатов гид­родинамических исследований. Предлагаемое решение имеет вид:

,

где .

При сравнении результатов полученных по приближенному и точному методам отмечается незначительная погрешность, особенно при протяженности ствола , что дает основание применять приближенный метод для графической обработки данных исследования.

При кривые восстановления давления могут обрабатываться методом касательной в координатах , а гидродинамические показатели могут быть рассчитаны по следующим формулам:

,

где i – угловой коэффициент;

в – отрезок, отсекаемый на оси ординат продолжением прямолинейного участка А ₀, определяемого по формуле вида:

,

где J ₁(t ₁) – параметр, соответствующий изменению забойного давления с начала остановки скважины на момент времени , который при больших временах или можно считать равным нулю.

При применимы другие методы обработки кривых восстановления давления, идентичных методам обработки гидропрослушивания вертикальных скважин:

Метод эталонных кривых.

,

где D Р _ф и t _ф – координаты фактической кривой, соответствующие единичным координатам эталонной кривой.

 

Дифференциальный метод.

,

где в – отрезок, отсекаемый на оси ординат .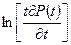

Интегральный метод.

,

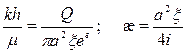где в – отрезок, отсекаемый на оси ординат .

В формулах дифференциального и интегрального методов наклон преобразованного графика рассматривается относительно оси абсцисс .

1.5. Интерпретация результатов гидродинамических исследований горизонтальных скважин при нестационарных режимах фильтрации (по В. А. Черных) [93,94,95]

Методы интерпретации результатов гидродинамических исследований горизонтальных скважин при нестационарных режимах фильтрации основаны на обработке кривых падения давления при постоянном дебите и восста­новления давления после остановки скважины. Первый из этих методов не получил широкого распространения, поскольку трудно выдержать режим постоянства отбора при изменяющемся давлении. Второй из этих методов является более простым и удобным, поэтому кривые восстановления дав­ления оказались наиболее доступным источником информации о пласте.

Интерпретация кривых восстановления давления может быть реализо­вана на основе интегрированной модели процесса, то есть аналитического ре­шения в самой общей форме. Однако в этом случае в процессе адаптации расчётных данных к реальным значениям потребуется многократное реше­ние задачи и создание специальных компьютерных программ. Кроме того, в случае применения интегрированной модели приходится считаться с не единственностью решения задачи и возможностью появления ложных ре­зультатов интерпретации даже при хорошем приближении к реальным дан­ным испытаний скважины. Поэтому далее будет использован сегментный подход, при котором уравнение восстановления давления записывается для каждого периода притока флюида к горизонтальному стволу. В отечествен­ной литературе этот метод был использован впервые в работах автора для обработки кривых восстановления давления в горизонтальных газовых скважинах на Оренбургском ГКМ. В соответствии с предлагаемой методи­кой обработку кривой восстановления давления необходимо начинать с выделения периодов притока на основе уравнений восстановления давления. В частности периоды радиального притока выделяются после обработки данных в координатах , а линейного при­тока , где р - давление в горизонтальном стволе; Z -коэффициент сверхсжимаемости газа; t - время работы скважины до её ос­тановки; t- время восстановления давления после остановки скважины. Наличие и время существования каждого периода определяется по нали­чию и размерам прямолинейного участка на кривых восстановления дав­ления в соответствующих координатах. Важнейшее значение при этом имеет угол наклона прямолинейного участка к временной оси. После выде­ления периодов течения можно начать определение параметров пласта по следующим формулам:

 

1-й период .

 

2-й период .

 

3-й период .

 

4-й период .

 

Здесь l - длина работающего интервала горизонтального ствола, k_х, k_y, k_z - проницаемости вдоль осей координат; m_пл - динамическая вязкость газа в пластовых условиях, T_пл, T_ат, р_пл, р_ат - температура и давление газа в пластовых и атмосферных условиях; Q_aт - объёмный дебит газа, приве­денный к атмосферным условиям; (a_п - угол наклона прямолинейного участка кривой восстановления давления к оси абсцисс; то есть времени; n - номер периода притока; h - работающая толщина пласта; m -пористость; b - размер залежи в направлении оси горизонтального ствола.

Интерпретация результатов гидродинамических исследований горизонтальных скважин при стационарных режимах фильтрации (по В.А. Черных). Известные в настоящее время уравнения притока газа к горизонтальным и многозабойным скважинам при линейном законе фильтрации можно пред­ставить в следующем виде:

и вести обработку результатов гидродинамических исследований в координатах ,

где – объемный дебит скважины, приведенный к стандартным условиям,

– текущее пластовое и забойное давления соответственно;

k – проницаемость;

m_ср –динамическая вязкость газа;

L – длина горизонтального ствола или суммарная длина боковых стволов многоствольной скважины;

р_ат –атмосферное давление;

z_cp – коэффициент сверхсжимаемости газа;

Т_пл, Т_ст – пластовая и стандартная температура;

f – функция, зависящая только от геометрических параметров пласта и скважины.

В случае фильтрации по закону Дарси все методики обработки ре­зультатов исследований на стационарных режимах фильтрации отличаются только формой функции f. Это позволяет использовать при обработке ре­зультатов исследований горизонтальных газовых скважин уравнения прито­ка, полученные для нефтяных скважин. В настоящее время для обработки результатов исследований горизонтальных газовых скважин на стационар­ных режимах фильтрации в основном применяется методика Алиева З.С.:

 

, (Алиев З.С.)

 

 

, (Меркулов В.П.)

 

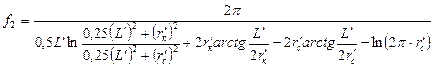, (Пилатовский В.П.)

 

, (Борисов Ю.П.)

 

, (Рейсс)

 

, (Джоши)

 

где ;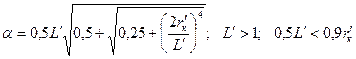

 

, (Ренард и Дюпюи)

 

, (Гайгер)

 

где

h – толщина продуктивного пласта;

L – длина горизонтального ствола;

r_с, r_к – радиусы горизонтального ствола и контура питания соответственно.

 

При проведении сравнительной оценки всех этих методик, необходимо рассмотреть результаты одного и того же ис­следования, то есть при одних и тех же значениях и . В этом случае должны выполнятся равенства ,где k ₀, k ₁,..., k ₇– значения проницаемости, получающиеся при обработке результатов исследования по различным методикам.

Из этих равенств следуют соотношения , которые позволяют оценить степень близости всех этих методик между собой. Как показывают расчёты, с увеличением длины горизонтального ствола разница между проницаемостями определёнными по этим методикам уменьшается (рис. 1.7). Этот результат является следствием того, что базовая методика (Алиев З.С.) разработана для горизонтального ствола полностью вскрывающего залежь. В качестве сравниваемых методов были взяты мето­ды Меркулова В.П., Пилатовского В.П., Борисова Ю.П., Рейсса, Джоши, Ренарда и Гайгера.

Рис. 1.7. Сравнительная оценка методов обработки результатов исследований горизонтальных скважин на стационарных режимах фильтрации (k₀ - проницаемость, полученная при обработке результатов исследований по методу Алиева 3. С.):

1 - соответствует обработке по формулам Лейбензона Л. С., Чарного И. А., Щелкачёва В.Н., 2 - Меркулова В. П., 3 - Пилатовского В. П.,

4 - Борисова Ю. П., Рейсса, Джоши, Ренарда, Дюпюи, Гайгера

 

Результаты расчётов показали, что методика Алиева З.С. очень близка к методике Меркулова В.П. (как было показано ранее, она полностью совпадает с методами Лейбензона Л.С. и Чарного И.А.). Разница между ними состоит в том, что первая группа методов (Алиев З.С. и др.) использует решения для бес­конечно длинного ствола, а вторая для горизонтального ствола конечной длины. Важно отметить, что в последнем случае на контуре питания под­держивалось постоянное давление, а, следовательно, и постоянный приток из окружающей области к горизонтальному стволу, что, конечно, увеличи­вало продуктивность горизонтального ствола. С другой стороны в первой группе методов этот поток считается равным нулю. Приве­денный анализ свидетельствует о том, что обработку результатов исследо­ваний горизонтальной газовой скважины на стационарных режимах фильт­рации необходимо проводить с использованием первой группы методов (Алиев З.С. и др.) для изолированной залежи, а по второй группе для залежей с проявлением водонапорного и упру­го-водонапорного режима разработки. Игнорирование этого требования при­водит к значительным ошибкам, в 2-5 раз, при расчёте проницаемости по данным гидродинамических исследований.

 

⇐ Предыдущая21222324252627282930Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: