 |
Примеры к контрольной работе № 2
|
|
|
|
Примеры к контрольной работе № 2
- Какие из следующих функций являются бесконечно малыми, бесконечно большими при
 (правило 2):
(правило 2):
а)  ;
; 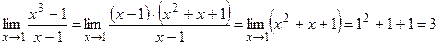
 имеет конечный предел при
имеет конечный предел при  .
.
б) 
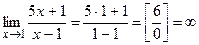
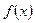 является бесконечно большой при
является бесконечно большой при 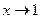 .
.
в) 

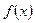 является бесконечно малой при
является бесконечно малой при 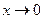 .
.
- Найти пределы функций. Пользуемся правилами 1, 2, 3, 4, 5.
а) 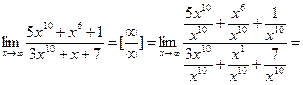
 , так как
, так как 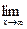
 ,
, 
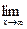
 ,
, 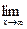
 ,
, 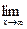
 .
.
б) 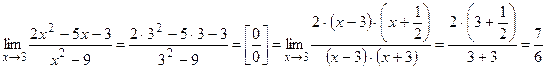 .
.
При этом разложим квадратный трёхчлен в числителе на множители 
 , где
, где  и
и  – корни,
– корни,  ,
, 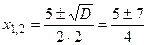 ;
;
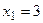 ;
;  ;
; 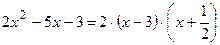 .
.
В знаменателе 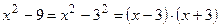 , т. к.
, т. к.  .
.

 в)
в) 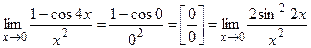 = Пусть
= Пусть  ,
,  ,
,  =
=
 .
.

 г)
г) 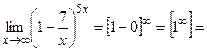 Пусть
Пусть  ,
,  ,
, 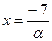 =
=
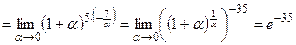 .
.
- Задана функция
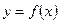 . Найти точки разрыва функции, если они существуют. Сделать чертёж.
. Найти точки разрыва функции, если они существуют. Сделать чертёж.

 – определена и непрерывна на всей числовой оси. Она может иметь разрывы в точках
– определена и непрерывна на всей числовой оси. Она может иметь разрывы в точках 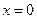 и
и  . Найдем односторонние пределы (слева и справа) в этих точках.
. Найдем односторонние пределы (слева и справа) в этих точках.











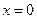 ;
;  ;
; 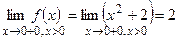 ;
; 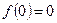 . Левый и правый пределы конечные, но не равны между собой;
. Левый и правый пределы конечные, но не равны между собой; 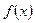 имеет в точке
имеет в точке 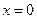 конечный разрыв скачок равен
конечный разрыв скачок равен 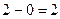 .
.
 ;
;  ;
;  ;
;  . Пределы слева и справа конечны и равны
. Пределы слева и справа конечны и равны  . В точке
. В точке 
 – непрерывна.
– непрерывна.
Задания к контрольной работе № 2
Содержит 3 контрольных задания:
1) Какие из следующих функций являются бесконечно малыми и бесконечно большими при  .
.
2) Найти пределы функции.
3) Задана функция 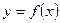 . Найти точки разрыва функции, если они существуют. Сделать чертеж.
. Найти точки разрыва функции, если они существуют. Сделать чертеж.
| № вар-та | Задания | № вар-та | Задания |
1) а)  ; б) ; б) 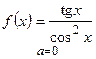 ;
в) ;
в)  .
2) а) .
2) а) 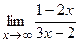 ; б) ; б)  ;
в) ;
в) 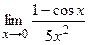 ; г) ; г)  .
3) .
3) 
| 1) а)  ; б) ; б) 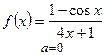 ;
в) ;
в)  .
2. а) .
2. а)  ; б) ; б)  ;
в) ;
в) 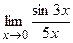 ; г) ; г)  .
3) .
3) 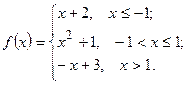
| ||
1) а) 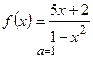 ; б) ; б)  ;
в) ;
в)  .
2) а) .
2) а) 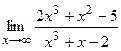 ; б) ; б)  ;
в) ;
в)  ; г) ; г)  .
3) .
3) 
| 1) а) 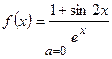 ; б) ; б)  ;
в) ;
в) 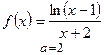 .
2) а) .
2) а)  ; б) ; б)  ;
в) ;
в) 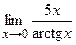 ; г) ; г)  .
3) .
3) 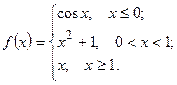
| ||
1) а) 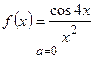 ; б) ; б)  ;
в) ;
в)  .
2) а) .
2) а) 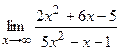 ; б) ; б)  ;
в) ;
в) 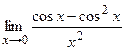 ; г) ; г) 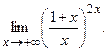 3)
3) 
| 1) а)  ; б) ; б) 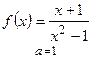 ;
в) ;
в)  .
2) а) .
2) а) 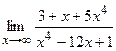 ; б) ; б)  ;
в) ;
в)  ; г) ; г)  3)
3) 
| ||
1) а)  ; б) ; б)  ;
в) ;
в)  .
2) а) .
2) а) 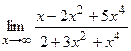 ; б) ; б)  ;
в) ;
в)  ; г) ; г)  3)
3) 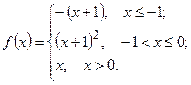
| 1) а)  ; б) ; б) 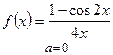 ;
в) ;
в)  .
2) а) .
2) а) 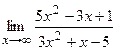 ; б) ; б)  ;
в) ;
в)  ; г) ; г) 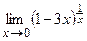 .
3) .
3) 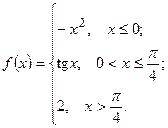
| ||
1) а)  ; б) ; б)  ;
в) ;
в) 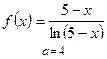 .
2) а) .
2) а)  ; б) ; б) 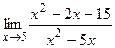 ;
в) ;
в) 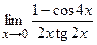 ; г) ; г) 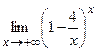 .
3) .
3) 
| 1) а) 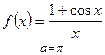 ; б) ; б)  ;
в) ;
в) 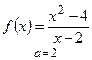 .
2) а) .
2) а) 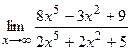 ; б) ; б) 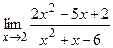 ;
в) ;
в)  ; г) ; г)  .
3) .
3) 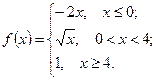
|
Контрольная работа № 3
|
|
|
Тема: Производные
Основные методические указания
1. Таблица основных производных
 ,
,  – функции от х
– функции от х
с, а, const – постоянные числа, 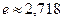
1–1)  ;
;
1–2) 

1–3) 

1–4) 

1–5) 
1–6) 
1–7) 

1–8) 
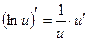
1–9) 
1–10) 
1–11) 
1–12) 
2. Основные правила дифференцирования
2–1) 
2–2) 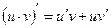
2–3) 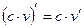 (с – число)
(с – число)
2–4) 
3. Производная функции, заданной параметрически

3–1) 
4. Производные высших порядков 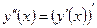 ,
, 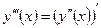 и так далее
и так далее
Чтобы найти производную второго порядка 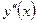 , надо сначала найти первую производную
, надо сначала найти первую производную  и затем найти производную от полученной функции.
и затем найти производную от полученной функции.
Примеры нахождения производных
1.  ;
; 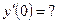
Применяем формулы 2–3, 1–3
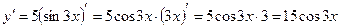 ,
, 
2. 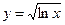
Применяем формулы 1–2, 1–8
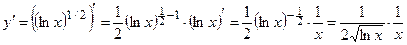
3.  ;
; 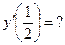
Применяем формулы 2–2, 1–2, 1–11

 ;
; 
4. 
Применяем формулы 2–4, 2–1, 1–7, 1–4
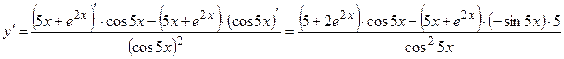
5. 
Применяем формулы 3–1, 1–3, 1–5, 1–7, 1–2
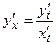

 ;
;

6. 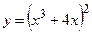
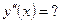
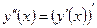
Найдем  :
:
Применяем формулы 1–1, 1–2, 2–1
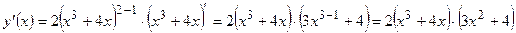
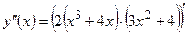
Применяем формулы 2–2, 2–3, 2–1, 1–1, 1–2
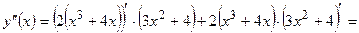

Задания к контрольной работе № 3
Контрольная работа содержит 6 заданий. В заданиях 1–5 надо найти производные функции  , в задании 6 – найти вторую производную
, в задании 6 – найти вторую производную 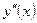 .
.
| № вар-та | Задания | № вар-та | Задания |
1) 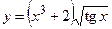 ; 2) ; 2) 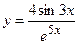 ;
3) ;
3) 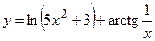 ; 4) ; 4)  ;
5) ;
5)  ; 6) ; 6) 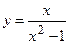 ; ; 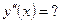
| 1)  ; 2) ; 2) 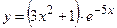 3)
3)  ; 4) ; 4)  ;
5) ;
5)  ; 6) ; 6) 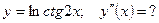
| ||
1) 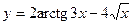 ; 2) ; 2)  ;
3) ;
3) 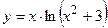 ; 4) ; 4)  ;
5) ;
5) 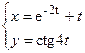 ; 6) ; 6) 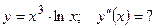
| 1) 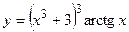 ; 2) ; 2)  ;
3) ;
3)  ; 4) ; 4) 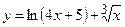 ;
5) ;
5)  ; 6) ; 6) 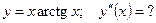
| ||
1)  ; 2) ; 2) 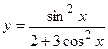 ;
3) ;
3) 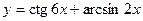 ; 4) ; 4) 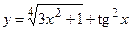 ;
5) ;
5) 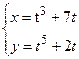 ; 6) ; 6) 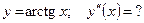
| 1)  ; 2) ; 2) 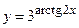 ;
3) ;
3) 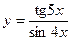 ; 4) ; 4) 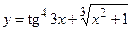 ;
5) ;
5) 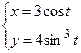 ; 6) ; 6) 
| ||
1)  ; 2) ; 2)  ;
3) ;
3) 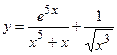 ; 4) ; 4)  ;
5) ;
5) 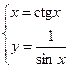 ; 6) ; 6) 
| 1)  ; 2) ; 2)  ;
3) ;
3)  ; 4) ; 4) 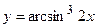 ;
5) ;
5) 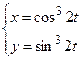 ; 6) ; 6) 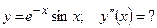
| ||
1) 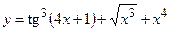 ;
2) ;
2) 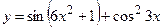 ;
3) ;
3)  ; 4) ; 4)  ;
5) ;
5) 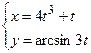 ; 6) ; 6) 
| 1)  ; 2) ; 2)  ;
3) ;
3)  ; 4) ; 4)  ;
5) ;
5)  ; 6) ; 6) 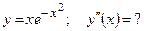
|
Контрольная работа № 4 
Исследование функций с помощью производных.
Контрольная работа №4 содержит 2 контрольных задания.
Краткая теория и методические указания для решения.
1. Правило Лопиталя для нахождения пределов функций в случае неопределенностей вида  или
или  .
.
Пусть функция 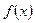 и
и  при
при 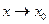 (или
(или  ) совместно стремятся к нулю или бесконечности. Если отношение их производных имеет предел, то отношение самих функций также имеет предел, равный пределу отношений производных, т. е.
) совместно стремятся к нулю или бесконечности. Если отношение их производных имеет предел, то отношение самих функций также имеет предел, равный пределу отношений производных, т. е.
|
|
|
пусть 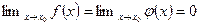

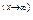
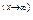
или 
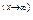
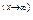
Тогда 
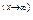
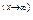
Если после первого применения правила Лопиталя получим опять  или
или  , то правило Лопиталя можно применить повторно.
, то правило Лопиталя можно применить повторно.
2. Общий план исследования функции и построение графика
При исследовании функции рекомендуется все результаты, полученные в каждом разделе плана наносить на координатную плоскость после каждого раздела.
I. Общая характеристика функции:
1. Область определения 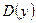 .
.
2. Характеристика функции (четность, нечетность).
3. Непрерывность функции. Точки разрыва.
4. Точки пересечения графика функции с осями координат

 (входит в область определения).
(входит в область определения).
5. Асимптоты.
1) Вертикальные асимптоты связаны с точками бесконечного разрыва 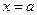 – вертикальная асимптота, если при
– вертикальная асимптота, если при 
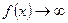 .
.
2) Наклонные асимптоты:  ,
,  ,
, 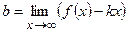 .
.
Полученные точки и асимптоты нанести на координатную плоскость.
II. Исследование функции на возрастание, убывание, экстремумы.
1. Находим производную  .
.
2. Определяем точки, где  или не существует.
или не существует.
3. Откладываем полученные точки на числовой оси и определяем знак производной 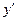 на каждом полученном интервале (для этого на каждом интервале можно взять любое значение х, подставить его в производную
на каждом полученном интервале (для этого на каждом интервале можно взять любое значение х, подставить его в производную  и определить знак результата).
и определить знак результата).
4. Определяем участки возрастания и убывания функции (по знаку 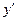 ).
).

 – функция возрастает
– функция возрастает
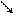
 – функция убывает
– функция убывает
5. Определяем точки экстремума – точки, где  и при переходе через эту точку производная меняет свой знак.
и при переходе через эту точку производная меняет свой знак.



 – максимум – минимум
– максимум – минимум
Вычисляем значение функции 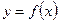 в полученных точках – экстремумы функции.
в полученных точках – экстремумы функции.
Точки экстремума нанести на координатную плоскость, сделать схематический график.
III. Исследование функции на выпуклость, вогнутость и точки перегиба.
1. Находим вторую производную 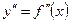
2. Определяем точки, где вторая производная равна нулю или не существует  .
.
|
|
|
3. Откладываем полученные точки на числовой оси и определяем знак второй производной на каждом полученном интервале (аналогично определению знака первой производной).
4. Определяем интервалы выпуклости и вогнутости функции (по знаку второй производной).
 – функция вогнутая
– функция вогнутая 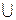
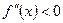 – функция выпуклая
– функция выпуклая 
5. Определяем точки перегиба – точки, где  и при переходе через эту точку
и при переходе через эту точку 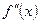 меняет знак (выпуклость меняется на вогнутость и наоборот). Вычисляем значения функции
меняет знак (выпуклость меняется на вогнутость и наоборот). Вычисляем значения функции 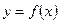 в точках перегиба.
в точках перегиба.
Точки перегиба нанести на схематический график и показать на графике выпуклость и вогнутость.
IV. Строим график.
Примеры решения заданий контрольной работы №4
Задание 1. Найти предел функции, пользуясь правилом Лопиталя
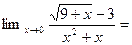
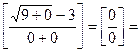
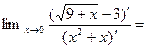
= 
Задание 2. Исследовать функцию  и построить ее график.
и построить ее график.
Решение. Будем следовать общему плану.
Построим координатную плоскость, на которую будем наносить результаты, полученные в каждом разделе.
I. Общая характеристика функции.
1. Область определения 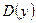 :
: 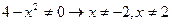
Т. е 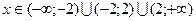
2. Характеристика функции.
Функция 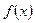 называется четной, если
называется четной, если  , нечетной, если
, нечетной, если  , иначе - функцией общего вида
, иначе - функцией общего вида
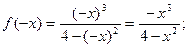
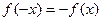
По определению, 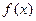 - нечетная функция.
- нечетная функция.
3. Непрерывность функции.
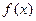 является непрерывной везде, кроме точек
является непрерывной везде, кроме точек 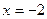 и
и 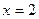 , где она терпит бесконечный разрыв.
, где она терпит бесконечный разрыв.
4. Точки пересечения графика функции с осями координат.

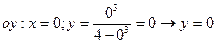
5. Асимптоты.
1. Вертикальные асимптоты связаны с точками бесконечного разрыва
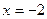 предел слева:
предел слева: 



предел справа: 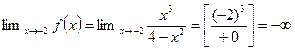


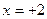 предел слева:
предел слева: 
|
|
|
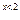
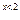
предел справа: 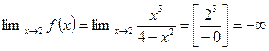


2. Наклонные асимптоты.
 ;
;  ;
; 

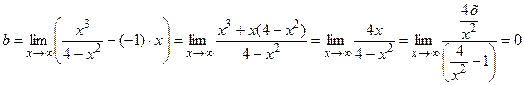
Наклонная асимптота 
При  и при
и при 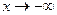 график функции
график функции  будет неограниченно приближаться к графику прямой
будет неограниченно приближаться к графику прямой  .
.
Полученные точки и асимптоты наносим на координатную плоскость.
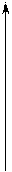











Схематический график 1.
II. Исследование функции на возрастание и убывание, экстремумы.
1. Находим

2. 
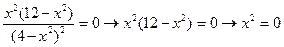
или 

 ,
, 
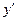 не существует, если
не существует, если  =0, т. е.
=0, т. е. 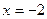 и
и 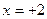 , но эти точки не входят в область определения.
, но эти точки не входят в область определения.
Нанесем полученные точки на ось 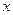











Определяем знак первой производной в каждом полученном интервале, для чего определим знак 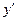 в произвольной точке каждого интервала.
в произвольной точке каждого интервала.
Возьмем, например, 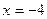 ,
,  ,
, 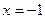 ,
,  ,
,  ,
,  .
.
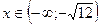
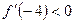
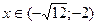

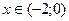

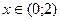

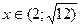



4. Определяем участки возрастания и убывания функции.

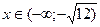

 функция убывает
функция убывает

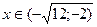
 функция возрастает
функция возрастает
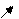
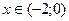
 функция возрастает
функция возрастает

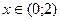
 функция возрастает
функция возрастает

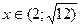
 функция возрастает
функция возрастает


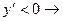 функция убывает
функция убывает
6. Определяем точки экстремума.


 Точка
Точка  -мининум
-мининум


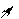 Точка
Точка 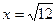 -максимум
-максимум


Нанесем точки экстремума на координатную плоскость.












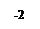





Схематический график 2.
III. Исследование функции на выпуклость, вогнутость и точки перегиба.
1. Находим вторую производную

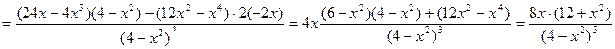
2. 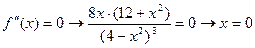
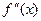 - не существует при
- не существует при  , т. е.
, т. е.


