 |
Таблица основных неопределённых интегралов
|
|
|
|
Таблица основных неопределённых интегралов
 – постоянные числа;
– постоянные числа;
 , если
, если 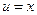 , то
, то 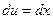 ;
;
1. 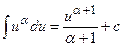
 ;
; 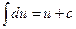 ; 1а.
; 1а.  ;
;
2.  ; 2а.
; 2а. 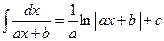 ;
;
3. 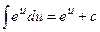 ; 3а.
; 3а. 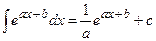 ;
;
4.  ;
;
5.  ; 5а.
; 5а.  ;
;
6. 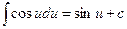 ; 6а.
; 6а.  ;
;
7.  ;
;
8.  ;
; 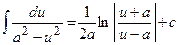 ;
;
9.  ;
;
10.  ; 10а.
; 10а.  ;
;
11.  ; 11а.
; 11а.  .
.
12.  ;
;
Формулы 1а, 2а, 3а, 5а, 6а, 10а, 11а получены по правилу 4.
Для взятия неопределённого интеграла, надо преобразовать подынтегральное выражение, воспользоваться правилами, чтобы привести его к табличным интегралам.
Контрольное задание № 2. Вычисление определённых и несобственных интегралов
а) Определённый интеграл по формуле Ньютона-Лейбница
 ,
,
где 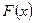 – первообразная функции
– первообразная функции 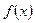 , т. е.
, т. е.  .
.
б) Несобственный интеграл по бесконечному промежутку

Если предел существует, то несобственный интеграл сходится и равен ему, иначе интеграл расходится.
Контрольное задание № 3. Приложение определённого интеграла для вычисления площади плоской фигуры.
Площадь плоской фигуры, ограниченной сверху графиком функции  , а снизу – графиком функции
, а снизу – графиком функции  при изменении х от а до b равна
при изменении х от а до b равна
 .
.
Примеры к контрольной работе № 6
Решение примеров к заданию I:
Применяя правило 2, формулы 1 и 2
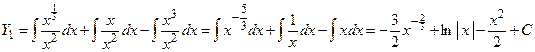 .
.
-
 ;
; 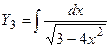 .
.
Выносим общий множитель в знаменателе, применим правило 3, формулы 7 и 9.
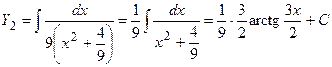
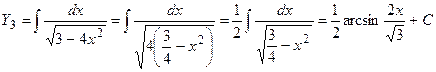 .
.
-
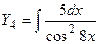 ;
;  ;
;  ;
;
Применим правило подведения под знак дифференциала 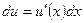 , правило 3 и формулы 10 (10а) и 2
, правило 3 и формулы 10 (10а) и 2
 .
.

 .
.
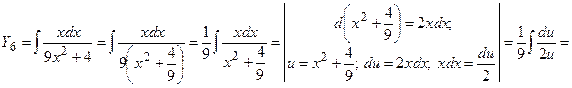
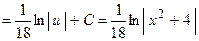 + С.
+ С.
-
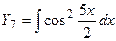 ;
;  ;
;  ;
;
Применяем формулы  ;
;  ;
;  , правила 3, 2 и формулы 6а, 1.
, правила 3, 2 и формулы 6а, 1.
 .
.
 .
.

Применим метод выделения полного квадрата в многочлене знаменателя, замену переменной, почленное деление дроби на знаменатель, подведение под знак дифференциала как в примере  , формулы 7 и 2. Так как
, формулы 7 и 2. Так как 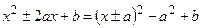 , то
, то
 ;
;
Замена переменной  , тогда
, тогда  ,
,  ;
;


 .
.
-
 ;
;
Применим правило 7 интегрирования по частям 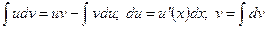 , формулы 6а, 5а
, формулы 6а, 5а
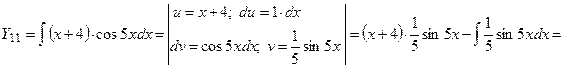
 .
.
Аналогичным способом находят интегралы от функций: 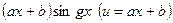 ;
;  ;
;  ;
; 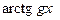
 ;
;  ; a, b, g – числа.
; a, b, g – числа.
|
|
|
-
 ;
;  ;
;
Применим замену переменных  , почленное деление дроби на знаменатель, правила 2 и 3, формулы 1, 8 и 2а.
, почленное деление дроби на знаменатель, правила 2 и 3, формулы 1, 8 и 2а.
 ;
;  ;
;  ;
;  ;
;

 .
.
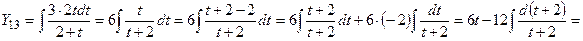
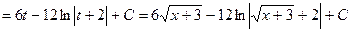 .
.
Решение примеров к заданию II:
1) Вычислить определённый интеграл
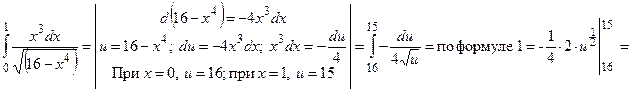
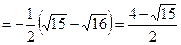
2) Вычислить несобственный интеграл или доказать расходимость.
 , где
, где 
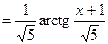 ;
;
 , т. к
, т. к  ;
;
Следовательно интеграл сходится и равен  .
.
Решение примеров к заданию III:
Вычислить площадь фигуры, ограниченной графиками функций  ;
; 
1) Построение схематического чертежа (см. как в контр. работе № 1, в задаче 3, стр. 3).
| х | ||||||
| у1 | ||||||
|
|
| |
| |
| |
|
| |
| |
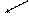

Фигура сверху ограничена  , снизу
, снизу  .
.
2) Точки пересечения двух кривых
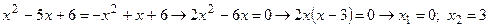
3) 
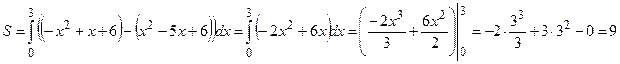 кв. ед.
кв. ед.
Задания к контрольной работе № 6
Содержит 3 контрольных задания:
I. Вычислить неопределённые интегралы.
II. а) Вычислить определённый интеграл
б) Вычислить несобственный интеграл или доказать его расходимость.
III. Вычислить площадь  фигуры, ограниченной графиками двух функций.
фигуры, ограниченной графиками двух функций.
| № вар-та | Задание | № вар-та | Задание |
| I. а) в) д) II. а) III. | I. а)  ; б) ; б)  ;
в) ;
в)  ; г) ; г)  ;
д) ;
д)  ; е) ; е) 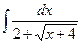 .
II. а) .
II. а)  ; б) ; б) 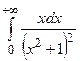 .
III. .
III. 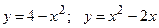 . .
| ||
| I. а) в) д) II. а) III. | I. а) 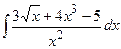 ; б) ; б)  ;
в) ;
в) 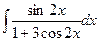 ; г) ; г)  ;
д) ;
д) 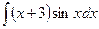 ; е) ; е) 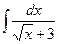 .
II. а) .
II. а)  ; б) ; б)  .
III. .
III. 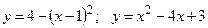 . .
| ||
| I. а) в) д) II. а) III. | I. а)  ; б) ; б)  ;
в) ;
в) 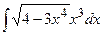 ; г) ; г)  ;
д) ;
д) 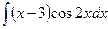 ; е) ; е) 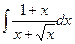 .
II. а) .
II. а) 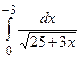 ; б) ; б) 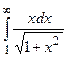 .
III. .
III. 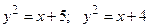 . .
| ||
| I. а) в) д) II. а) III. | I. а)  ; б) ; б)  ;
в) ;
в)  ; г) ; г)  ;
д) ;
д) 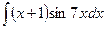 ; е) ; е)  .
II. а) .
II. а)  ; б) ; б)  .
III. .
III. 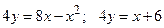 . .
| ||
| I. а) в) д) II. а) III. | I. а)  ; б) ; б) 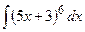 ;
в) ;
в)  ; г) ; г) 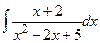 ;
д) ;
д)  ; е) ; е) 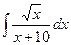 .
II. а) .
II. а) 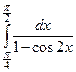 ; б) ; б) 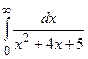 .
III. .
III.  . .
|
Литература
1. Щипачев В. П. Высшая математика. М. Высшая школа. 1982-2003 гг.
|
|
|
2. Кудрявцев В. А., Демидович Б. П. Курс высшей математики. М. Наука. 1975-1992 гг.
3. Письменный Д. Конспект лекций по высшей математике. I часть. Айрис Пресс Рольф. М. 2000 г.
4. Данко П. Е. и др. Высшая математика в упражнениях и задачах. М. Высшая школа. 1980-2006 гг.
5. Запорожец Г. И. Руководство к решению задач по математическому анализу. М. Высшая математика. 1964 г.
6. Пискунов Н. С. Дифференциальное и интегральное исчисление. М. Наука. 1970-2000 гг.
7. Богомолов. Практические занятия по математике. М. 1983г.
8. Методические указания к контрольным работам кафедры математики РГГРУ.
Номер варианта каждой контрольной работы совпадает с последней цифрой учебного номера студента (номера зачетной книжки).
|
|
|





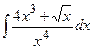 ; б)
; б)  ;
;  ; г)
; г) 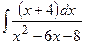 ;
;  ; е)
; е) 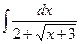 .
.  ; б)
; б)  .
.  .
.  ; б)
; б)  ;
;  ; г)
; г) 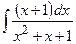 ;
;  ; е)
; е) 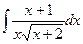 .
.  ; б)
; б)  .
. 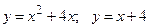 .
.  ; б)
; б) 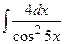 ;
; 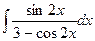 ; г)
; г)  ;
;  ; е)
; е) 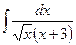 .
.  ; б)
; б)  .
.  .
. 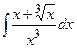 ; б)
; б) 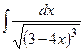 ;
;  ; г)
; г)  ;
; 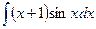 ; е)
; е) 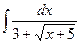 .
. 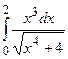 ; б)
; б)  .
. 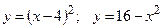 .
.  ; б)
; б)  ;
;  ; г)
; г)  ;
; 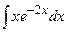 ; е)
; е)  .
.  ; б)
; б)  .
.  .
.