|
Решение некоторых типовых примеров
|
|
|
|
Решение некоторых типовых примеров
и методические указания по контрольной работе
- Даны две точки:
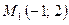 в декартовой системе координат,
в декартовой системе координат,  – в полярной системе координат.
– в полярной системе координат.
 |
|
| |||||
|


|
|
 | |||
 | |||
Полярные координаты т. 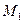 : :
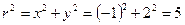
 ; ; 
 ; ; 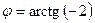 ; ;
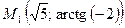
| Декартовы координаты т. 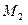 : :
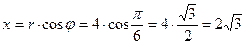
 ; ; 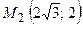
|
- Линия задана уравнением
 . Для того, чтобы построить график рекомендуется составить таблицу значений
. Для того, чтобы построить график рекомендуется составить таблицу значений  для угла
для угла  , значения через промежуток
, значения через промежуток  , отложить полученные точки
, отложить полученные точки 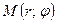 на плоскости и соединить их плавной линией (подробно построение графиков рассмотрено в методическом пособии стр. 5-6).
на плоскости и соединить их плавной линией (подробно построение графиков рассмотрено в методическом пособии стр. 5-6). - Дано уравнение прямой
 .
.
1) уравнение этой прямой можно привести к уравнению с угловым коэффициентом:  ,
,  – угол наклона прямой к оси ОХ.
– угол наклона прямой к оси ОХ.
2) Написать уравнение прямой, проходящей через точку  и а) параллельной данной прямой, б) перпендикулярной данной прямой.
и а) параллельной данной прямой, б) перпендикулярной данной прямой.
Уравнение прямой через точку 
 ;
;
Условие параллельности  ;
;
Условие перпендикулярности  ;
;
3) Уравнение прямой, проходящей через точку  и
и 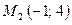 .
.
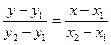 ;
;  ;
; 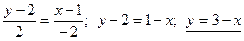 .
.
4) Пример вычисления определителя разложением по строке или столбцу.
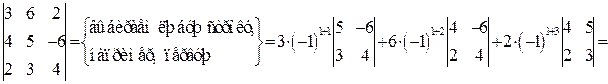

5) Решение системы уравнений по правилу Крамера.

Составим и вычислим основной определитель системы, составленный из коэффициентов при
неизвестных. Будем его вычислять, используя разложение, так как она содержит нулевой
элемент и это упростит вычисления.
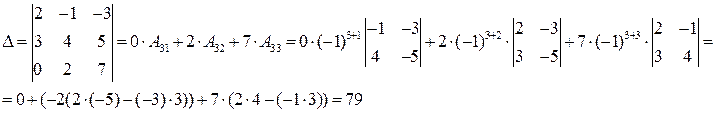
Основной определитель системы не равен 0  , следовательно, система имеет единственное решение.
, следовательно, система имеет единственное решение.
Для нахождения решения составим вспомогательные определения 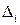 , которые получаются из основного определителя заменой в нем
, которые получаются из основного определителя заменой в нем 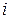 -го столбца столбцом свободных членов исходной системы.
-го столбца столбцом свободных членов исходной системы.
|
|
|
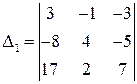 (вычислим, используя разложение по первой строке)
(вычислим, используя разложение по первой строке) 
Определители  и
и  вычислим используя разложения по первому столбцу.
вычислим используя разложения по первому столбцу.
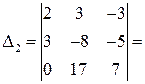


6) Даны два вектора 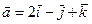 ,
, 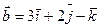 . Найти площадь параллелограмма, построенного на этих векторах
. Найти площадь параллелограмма, построенного на этих векторах  .
.

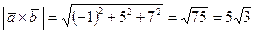 кв. ед.
кв. ед.
Задания к контрольной работе № 5
Контрольная работа содержит 5 заданий:
- Даны 2 точки
 в декартовой системе координат и точка
в декартовой системе координат и точка  в полярной системе координат. Построить эти точки. Определить полярные координаты точки
в полярной системе координат. Построить эти точки. Определить полярные координаты точки 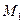 и декартовы координаты точки
и декартовы координаты точки 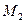 .
. - Задана линия
 .
.
а) Построить эту линию по точкам от  до
до 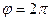 , придавая
, придавая  значения через
значения через  .
.
б) Найти уравнение этой линии в декартовой системе координат.
- Дано уравнение первой прямой
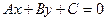 и точки
и точки  и
и  .
.
а) привести уравнение первой прямой к виду  и определить угол наклона прямой к оси х,
и определить угол наклона прямой к оси х,
б) написать уравнение первой прямой в отрезках,
в) написать уравнение второй прямой, проходящей через точку М и параллельной I прямой,
г) написать уравнение третьей прямой, проходящей через точку М и перпендикулярной I прямой,
д) написать уравнение четвертой прямой  , проходящей через точки
, проходящей через точки  и
и  ,
,
е) найти точку пересечения первой и четвертой прямых,
ж) построить все четыре прямые.
- Решить систему линейных уравнений, используя формулу Крамера. Вычисление определителей производить разложением по строке или столбцу.
- Даны вектора
 ,
,  ,
,  и
и  . Найти:
. Найти:
а) скалярное произведение 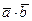 ,
,
б) угол между векторами  и
и 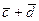 ,
,
в) векторное произведение векторов 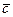 и
и 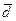 и площадь параллелограмма, построенного на них
и площадь параллелограмма, построенного на них
| № вар-та | Задания |
| 1. | 1)  2) 2)  ; 3) ; 3) 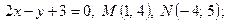 4) 4) 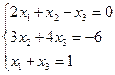 ; 5) ; 5) 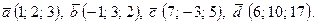
|
| 2. | 1) 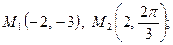 2) 2) 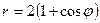 ; 3) ; 3) 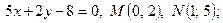 4) 4)  ; 5) ; 5) 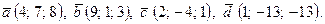
|
| 3. | 1)  2) 2)  ; 3) ; 3)  4) 4)  ; 5) ; 5) 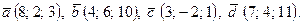
|
| 4. | 1) 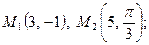 2) 2)  ; 3) ; 3) 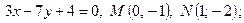 4) 4)  ; 5) ; 5) 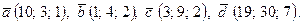
|
| 5. | 1)  2) 2)  ; 3) ; 3) 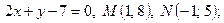 4) 4) 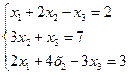 ; 5) ; 5) 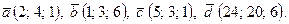
|
| 6. | 1)  2) 2) 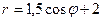 ; 3) ; 3) 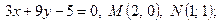 4) 4) 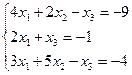 ; 5) ; 5) 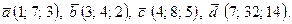
|
| 7. | 1)  2) 2) 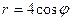 ; 3) ; 3)  4) 4) 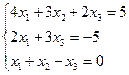 ; 5) ; 5) 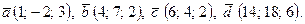
|
| 8. | 1)  2) 2) 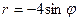 ; 3) ; 3)  4) 4)  ; 5) ; 5) 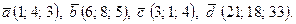
|
| 9. | 1) 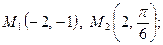 2) 2)  ; 3) ; 3) 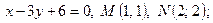 4) 4)  ; 5) ; 5) 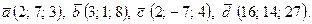
|
| 10. | 1)  2) 2) 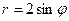 ; 3) ; 3)  4) 4)  ; 5) ; 5) 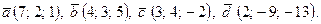
|
|
|
|
Контрольная работа № 6
Тема: «Неопределённые и определённые интегралы»
Краткая теория и формулы:
Контрольная работа содержит три контрольных задания.
Контрольное задание № 1. Вычисление неопределённого интеграла
I. Неопределенный интеграл есть
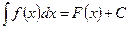 , где
, где  , С – постоянная
, С – постоянная  .
.
 называется первообразной для
называется первообразной для 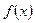 .
.
Основные правила интегрирования:
1. Дифференциал функции  ;
;  .
.
2. 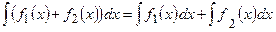 .
.
3.  (a – число).
(a – число).
4. Если 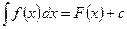 , то
, то 
 .
.
5. Если 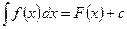 , а
, а  , то
, то  .
.
6. Метод интегрирования по частям: если  ,
,  , то
, то  .
.
7. Правильность результатов интегрирования проверяется так: 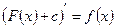 . Взятие неопределённого интеграла есть действие, обратное взятию производной.
. Взятие неопределённого интеграла есть действие, обратное взятию производной.
|
|
|