 |
Формулировка задания и его объём
|
|
|
|
Федеральное государственное бюджетное образовательное учреждение
Высшего профессионального образования
«Ростовский государственный университет путей сообщения»
(филиал РГУПС в г.Минеральные Воды)
А.Д. Омарова
КОНТРОЛЬНАЯ РАБОТА № 1
По дисциплине «Математика»
Для студентов специальностей
Подвижной состав железных дорог
Эксплуатация железных дорог
Учебно-методическое пособие
Минеральные Воды, 2014
УДК 512.2 (07.5.6)
В разработку включены методические указания и задания к контрольной работе №1 для студентов очной и заочной форм обучения специальностей:190300.65 Подвижной состав железных дорог, 190401.65 Эксплуатация железных дорог.
Методические указания содержат теоретический материал и примеры решения типовых задач.
Составитель: канд. физ.-мат. наук, доцент Омарова А.Д.
Рецензент: канд. физ.-мат. наук, доцент Кабакова Е.В.
СОДЕРЖАНИЕ
| 1. ВВЕДЕНИЕ……………………………………………………………. | |
| 2. СОДЕРЖАНИЕ КОНТРОЛЬНОЙ РАБОТЫ ПО ТЕМАМ ПРОГРАММЫ ДИСЦИПЛИНЫ……………………………………………. | |
| 3. ФОРМУЛИРОВКА ЗАДАНИЯ И ЕГО ОБЪЕМ…………………… | |
| 4. ПОРЯДОК ВЫБОРА ТЕМЫ И ОСВЕЩЕНИЯ ПРОБЛЕМЫ…… | |
| 5. СТРУКТУРА КОНТРОЛЬНОЙ РАБОТЫ, ОБЩИЕ ТРЕБОВАНИЯ К ЕЕ НЕПИСАНИЮ…………………………………………………. | |
| 6. Рекомендации по организации выполнения контрольной работы, примерный календарный план его выполнения………………………………………………… | |
| 6.1. Линейная алгебра. Аналитическая геометрия……………………. | |
| 6.2. Введение в математический анализ………………………………… | |
| 6.3. Производная и дифференциал функции. Применение производных к исследованию свойств функций……………………………… | |
| 6.4. Функции нескольких переменных…………………………………. | |
| 7. Порядок защиты и ответственность студента за выполнение контрольной работы………………………. | |
| 8. Список рекомендуемой литературы…………………… |
|
|
|
ВВЕДЕНИЕ
Дисциплина «Математика» имеет цель ознакомить студентов с основами высшей математики как средства решения теоретических и практических задач. Помимо этого, она дает знания, необходимые для изучения других естественнонаучных и инженерных дисциплин, которые преподаются параллельно с математикой или на последующих курсах.
При выполнении практических занятий необходимо выработать навыки логического и аналитического мышления, приобрести вычислительные навыки.
СОДЕРЖАНИЕ КОНТРОЛЬНОЙ РАБОТЫ
ПО ТЕМАМ ПРОГРАММЫ ДИСЦИПЛИНЫ
Контрольная работа выполняется по темам: Линейная алгебра. Аналитическая геометрия. Введение в математический анализ. Производная и дифференциал функции. Применение производных к исследованию свойств функций. Функции нескольких переменных.
Формулировка задания и его объём
Задание 1. По координатам вершин пирамиды А1А2А3А4 найти: 1) длины ребер А1А2 и А1А3; 2) угол между ребрами А1А2 и А1А3; 3) площадь грани А1А2А3; 4) объем пирамиды; 5) уравнения прямых А1А2 и А1А3; 6) уравнения плоскостей А1А2А3 и А1А2А4; 7) угол между плоскостями А1А2А3 и А1А2А4; 8) сделать чертеж.
1. А1(–1;2;1), А2(–2;2;5), А3(–3;3;1), А4(–1;4;3).
2. А1(–2;1;–1), А2(–3;1;3), А3(–4;2;–1), А4(–2;3;1).
3. А1(1;1;2), А2(0;1;6), А3(–1;2;2), А4(1;3;4).
4. А1(–1;–2;1), А2(–2;–2;5), А3(–3;-1;1), А4(–1;0;3).
5. А1(2;–1;1), А2(1;–1;5), А3(0;0;1), А4(2;1;3).
6. А1(–1;1;–2), А2(–2;1;2), А3(–3;2;–2), А4(–1;0;3).
7. А1(1;2;1), А2(0;2;5), А3(–1;3;1), А4(1;4;3).
8. А1(–2;–1;1), А2(–3;–1;5), А3(–4;0;1), А4(–2;1;3).
9. А1(1;–1;2), А2(0;–1;6), А3(–1;0;2), А4(1;1;4).
10. А1(1;–2;1), А2(0;–2;5), А3(–1;–1;1), А4(1;0;3).
11. А1(0;3;2), А2(–1;3;6), А3(–2;4;2), А4(0;5;4).
|
|
|
12. А1(–1;2;0), А2(–2;2;4), А3(–3;3;0), А4(–1;4;2).
13. А1(2;2;3), А2(1;2;7), А3(0;3;3), А4(2;4;5).
14. А1(0;–1;2), А2(–1;–1;6), А3(–2;0;2), А4(0;1;4).
15. А1(3;0;2), А2(2;0;6), А3(1;1;2), А4(3;2;4).
16. А1(0;2;–1), А2(–1;2;3), А3(–2;3;7), А4(0;4;1).
17. А1(2;3;2), А2(1;3;6), А3(0;4;2), А4(2;5;4).
18. А1(–1;0;2), А2(–2;0;6), А3(–3;1;2), А4(–1;2;4).
19. А1(2;0;3), А2(1;0;7), А3(0;1;3), А4(2;2;5).
20. А1(2;–1;2), А2(1;–1;6), А3(0;0;2), А4(2;1;4).
Задание 2. Дана система трех линейных уравнений с тремя неизвестными. Требуется: 1) найти ее решение с помощью формул Крамера; 2) записать систему в матричной форме и решить ее средствами матричного исчисления. Проверить правильность вычисления обратной матрицы используя матричное умножение.
1. 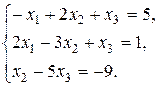
 2.
2. 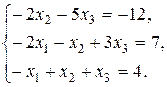
3. 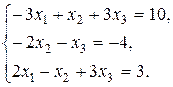 4.
4. 
5. 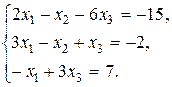 6.
6. 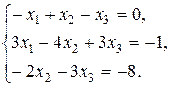
7.  8.
8. 
9.  10.
10. 
11. 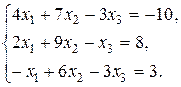 12.
12. 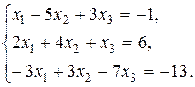
13. 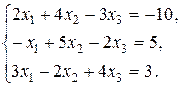 14.
14. 
15.  16.
16. 
17. 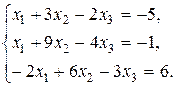 18.
18. 
19. 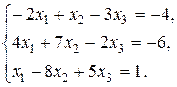 20.
20. 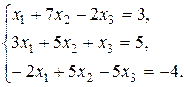
Задание 3. Найти множество решений однородной системы трех линейных уравнений с четырьмя неизвестными.
1.  2.
2. 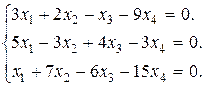
3. 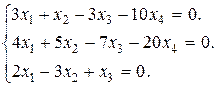 4.
4. 
5. 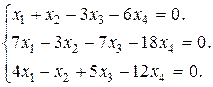 6.
6. 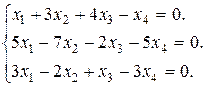
7. 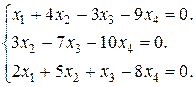 8.
8. 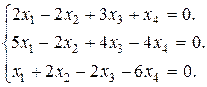
9. 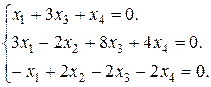 10.
10. 
11. 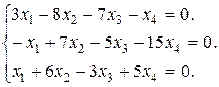 12.
12. 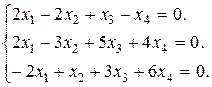
13. 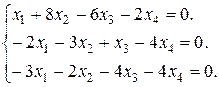 14.
14. 
15.  16.
16. 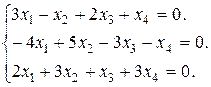
17. 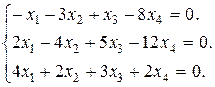 18.
18. 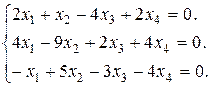
19. 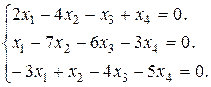 20.
20. 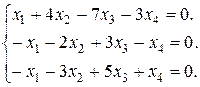
Задание 4. Определить собственные значения и собственные векторы матрицы третьего порядка.
1.  , 2.
, 2. 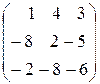 , 3.
, 3.  , 4.
, 4.  ,
,
5. 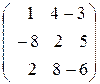 , 6.
, 6.  , 7.
, 7.  , 8.
, 8. 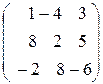 ,
,
9.  , 10.
, 10.  , 11.
, 11. 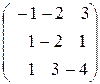 , 12.
, 12.  ,
,
13. 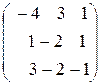 , 14.
, 14.  , 15.
, 15. 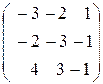 , 16.
, 16. 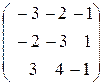 ,
,
17.  , 18.
, 18. 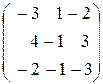 , 19.
, 19.  , 20.
, 20. 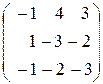 .
.
Задание 5. Вычислить пределы функций.
1.  . .
| 2.  . .
|
3. 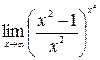 . .
| 4. 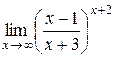 . .
|
5.  . .
| 6. 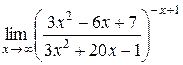 . .
|
7. 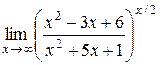 . .
| 8. 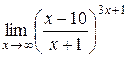 . .
|
9.  . .
| 10.  . .
|
11. 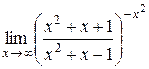 . .
| 12. 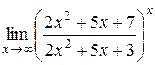 . .
|
13.  . .
| 14.  . .
|
15. 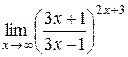 . .
| 16. 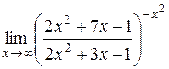 . .
|
17. 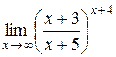 . .
| 18. 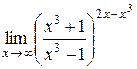 . .
|
19.  . .
| 20.  . .
|
Задание 6. Вычислить пределы функций.
1. 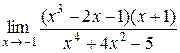 . .
| 2. 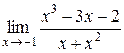 . .
|
3.  . .
| 4. 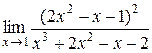 . .
|
5.  . .
| 6. 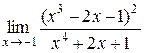 . .
|
7.  . .
| 8. 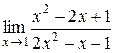 . .
|
9. 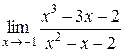 . .
| 10. 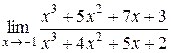 . .
|
11.  . .
| 12.  . .
|
13. 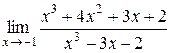 . .
| 14. 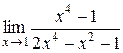 . .
|
15. 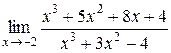 . .
| 16. 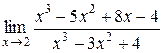 . .
|
17.  . .
| 18.  . .
|
19.  . .
| 20. 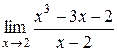 . .
|
Задание 7. Вычислить пределы функций.
1. 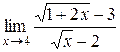 . .
| 2. 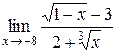 . .
|
3. 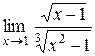 . .
| 4. 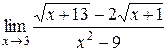 . .
|
5.  . .
| 6. 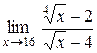 . .
|
7. 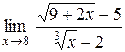 . .
| 8. 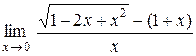 . .
|
9.  . .
| 10. 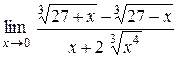 . .
|
11.  . .
| 12.  . .
|
13.  . .
| 14. 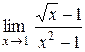 . .
|
15. 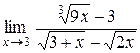 . .
| 16. 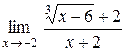 . .
|
17. 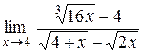 . .
| 18. 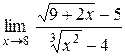 . .
|
19. 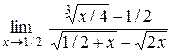 . .
| 20. 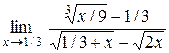 . .
|
Задание 8. Вычислить пределы функций.
1. 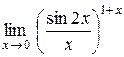 . .
| 2. 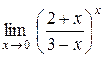 . .
|
3.  . .
| 4. 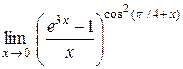 . .
|
5.  . .
| 6.  . .
|
7.  . .
| 8.  . .
|
9. 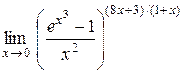 . .
| 10.  . .
|
11. 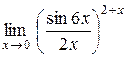 . .
| 12. 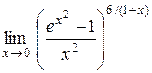 . .
|
13. 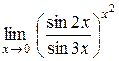 . .
| 14. 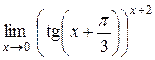 . .
|
15.  . .
| 16. 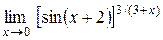 . .
|
17. 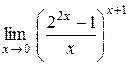 . .
| 18. 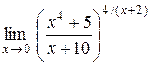 . .
|
19. 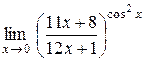 . .
| 20. 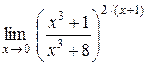 . .
|
Задание 9. Найти производную.
1. 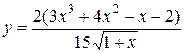 . .
| 2.  . .
|
3. 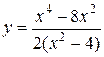 . .
| 4. 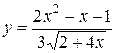 . .
|
5. 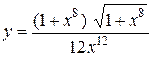 . .
| 6. 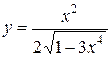 . .
|
7.  . .
| 8. 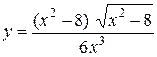 . .
|
9.  . .
| 10.  . .
|
11. 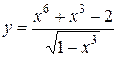 . .
| 12. 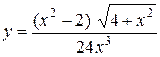 . .
|
13. 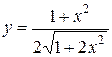 . .
| 14. 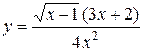 . .
|
15. 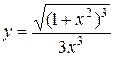 . .
| 16. 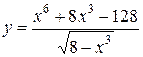 . .
|
17. 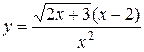 . .
| 18. 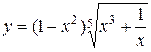 . .
|
19. 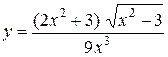 . .
| 20. 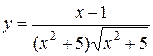 . .
|
Задание 10. Найти производную.
1. 
2. 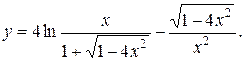
3. 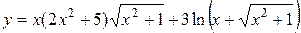 .
.
4. 
5. 
6. 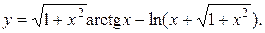
7. 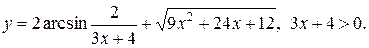
8. 
9. 
10. 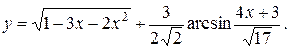
11. 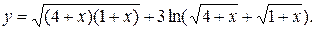
12. 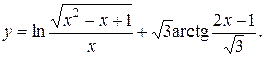
13. 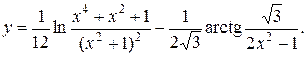
14. 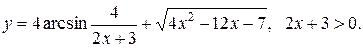
15. 
16. 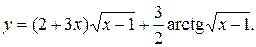
17. 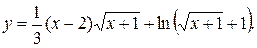
18. 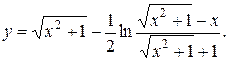
19. 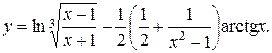
20. 
Задание 11. Найти производную 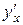 .
.
1. 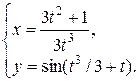
| 2. 
|
3. 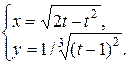
| 4. 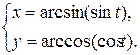
|
5. 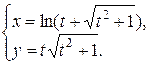
| 6. 
|
7. 
| 8. 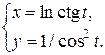
|
9. 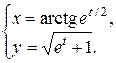
| 10. 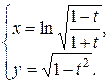
|
11. 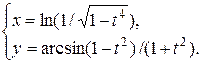
| 12. 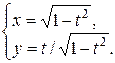
|
13. 
| 14. 
|
15. 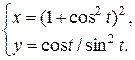
| 16. 
|
17. 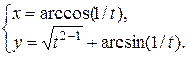
| 18. 
|
19. 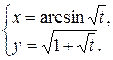
| 20. 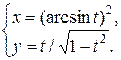
|
Задание 12. Найти производную указанного порядка.
1. 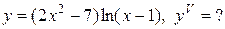
| 2. 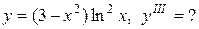
|
3. 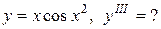
| 4. 
|
5. 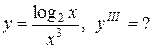
| 6. 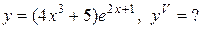
|
7. 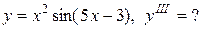
| 8. 
|
9. 
| 10. 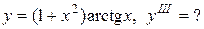
|
11. 
| 12. 
|
13. 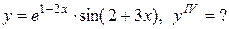
| 14. 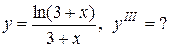
|
15. 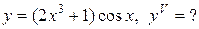
| 16. 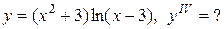
|
17. 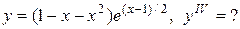
| 18. 
|
19. 
| 20. 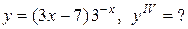
|
Задание 13. Исследовать функцию y=f(x) на непрерывность: найти точки разрыва функции и определить их тип. Построить схематический график функции.
1. 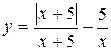 . 2.
. 2. 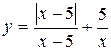 .
.
3. 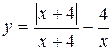 . 4.
. 4. 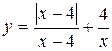 .
.
5. 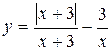 . 6.
. 6. 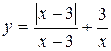 .
.
7. 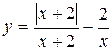 . 8.
. 8. 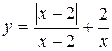 .
.
|
|
|
9.  . 10.
. 10. 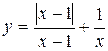 .
.
11. 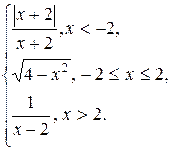 12.
12. 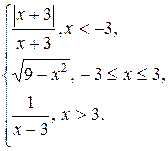
13. 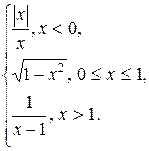 14.
14. 
15. 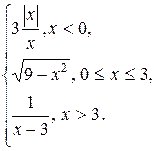 16.
16. 
17. 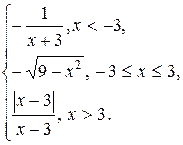 18.
18. 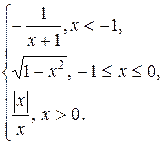
19. 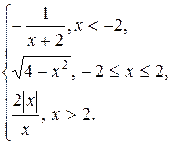 20.
20. 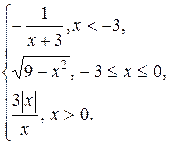
Задание 14. Вычислить предел функции с помощью правила Лопиталя.
1.  2.
2. 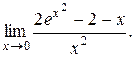
3.  4.
4. 
5.  6.
6. 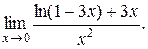
7. 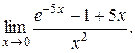 8.
8. 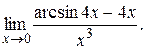
9. 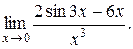 10.
10. 
11.  12.
12. 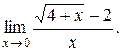
13. 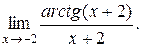 14.
14. 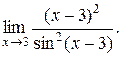
15.  16.
16. 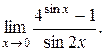
17.  18.
18. 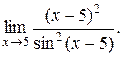
19. 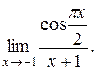 20.
20. 
Задание 15. Построить график функции y=f(x), используя общую схему исследования функции.
1. 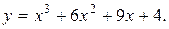 2.
2. 
3. 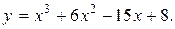 4.
4. 
5. 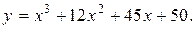 6.
6. 
7.  8.
8. 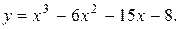
9. 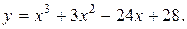 10.
10. 
11. 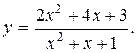 12.
12. 
13. 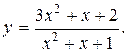 14.
14. 
15.  16.
16. 
17.  18.
18. 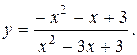
19. 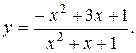 20.
20. 
Задание 16. Найти частные производные второго порядка функции многих переменных.
1. 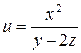 .
2. .
2. 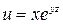 .
3. .
3.  .
4. .
4. 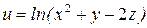 .
5. .
5. 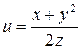 .
6. .
6.  .
7. .
7.  .
8. .
8. 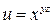 .
9. .
9.  .
10. .
10. 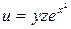 . .
| 11.  .
12. .
12.  .
13. .
13. 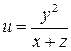 .
14. .
14.  .
15. .
15. 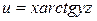 .
16. .
16. 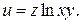 17.
17. 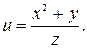 18.
18. 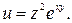 19.
19. 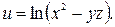 20.
20. 
|
|
|
|


