Линейная алгебра. Аналитическая геометрия.

1. Определение. Определителем или детерминантом n-го порядка называется число D, равное алгебраической сумме n! членов, составленных определенным образом из элементов a_ij определителя.

Обозначение: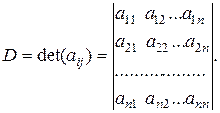

Определение. Алгебраическим дополнением A_ij элемента a_ij определителя n- го порядка называется определитель (n –1 )- го порядка, полученный из исходного вычеркиванием i -й строки и j- го столбца и умноженный на (–1) ^i+j.

Рекуррентная формула для вычисления определителя n- го порядка имеет вид:

D = a_n1A_n1+ a_n2A_n2+…+ a_nnA_nn

(разложение определителя по элементам n- ой строки).

Определитель второго порядка

2. Определение. Скалярным произведением двух векторов и называется число, определяемое равенством:

,

где – угол между векторами и .

3. Определение. Векторным произведением двух векторов и называется вектор удовлетворяющий следующим свойствам:

1) вектор перпендикулярен к обоим перемножаемым векторам (рисунок 1);

2) длина вектора равна площади параллелограмма построенного на перемножаемых векторах как на сторонах ();

3) направление вектора таково, что поворот совершающийся от вектора к вектору , виден совершающимся против часовой стрелки.

 

 

 

 

Рисунок 1. Рисунок 2.

 

В координатной форме векторное произведение векторов вычисляется по формуле:

.

4. Определение. Смешанным произведением трех векторов , и называется число, определяемое следующим образом:

.

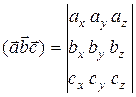Модуль смешанного произведения векторов равен объему параллелепипеда построенного на перемножаемых векторах, как на ребрах.

5. Общее уравнение плоскости Р имеет вид:

Ax + By + Cz + D = 0,

где – нормальный вектор плоскости (рисунок 2).

Уравнение плоскости, проходящее через три заданные точки M₀(x₀;y₀;z₀), M₁(x₁;y₁;z₁) и M₂(x₂;y₂;z₂), имеет вид:

.

Угол между двумя плоскостями, имеющими нормальные векторы и , определяется как угол между этими векторами по формуле скалярного произведения векторов:

.

6. Уравнения прямой в пространстве, проходящей через две заданные точки M₀(x₀;y₀;z₀) и M₁(x₁;y₁;z₁), имеют вид:

.

7. Определение. Матрицей A=(a_ij) размера m n называется прямоугольная таблица чисел, состоящая из m строк и n столбцов:

.

Определение. Произведением матрицы A=(a_ij) размера m r на матрицу B=(b_jk) размера r n называется матрица C=AB=(c_ik) размера m n с элементами

c_ik=a_i1b_1k+a_i2b_2k+…+a_irb_rk

(поэлементарное умножение i -й строки матрицы А на k -й столбец матрицы В).

Определение. Матрица размера n n называется квадратной матрицей n -го порядка. Элементы a₁₁,a₂₂,…,a_nn образуют главную диагональ матрицы.

Определение. Определитель, составленный из элементов квадратной матрицы, называется определителем (или детерминантом) матрицы и обозначается или det A.

Определение. Матрица Е с элементами 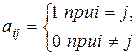называется единичной матрицей п -го порядка.

Определение. Матрица А^-1 называется обратной к матрице А ( det A 0), если

А^-1А=АА^-1=Е.

Обратная матрица вычисляется по формуле:

,

где D_A – определитель матрицы А,

А_ij – алгебраическое дополнение элемента а_ij.

8. Определение. Матрица A_r называется канонической, если в начале ее главной диагонали стоят единицы, а все остальные элементы равны нулю.

Например:

.

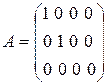Любая матрица может быть приведена к каноническому виду путем элементарных преобразований:

а) перестановки столбцов (строк);

б) умножения столбца (строки) на число, отличное от нуля;

в) прибавления к элементам какого-либо столбца (строки) соответствующих элементов другого столбца (строки), умноженных на одно и тоже число.

Определение. Матрицы, переходящие друг в друга в результате элементарных преобразований, называются эквивалентными.

Определение. Число r единиц, стоящих на главной диагонали канонической матрицы A_r, не зависит от способа приведения матрицы А к каноническому виду и называется рангом исходной матрицы А и обозначается: r(A)=r. Эквивалентные матрицы имеют один и тот же ранг.

9. Система трех линейных уравнений с тремя неизвестными имеет вид:

где a_ij – коэффициенты системы; b_i -– свободные члены.

Определение. Определитель третьего порядка , составленный из коэффициентов при неизвестных, называется определителем системы. Если , то единственное решение данной системы выражается формулами Крамера:

где 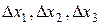– определители третьего порядка, получаемые из определителя системы заменой столбцов коэффициентов при x₁, x₂, x₃ столбцом свободных членов b₁, b₂, b₃.

Приведенную систему можно записать в матричной форме следующим образом:

AX=B, или

Решение системы в матричной форме имеет вид:

X=A^-1B,

если определитель системы отличен от нуля.

Если система линейных уравнений с n неизвестными совместна, а ранг матрицы системы меньше числа неизвестных, т.е. r<n, то система имеет бесчисленное множество решений. Свободные n-r неизвестных выбираются произвольно, а главные r неизвестных определяются единственным образом через свободные неизвестные.

10. Определение. Вектор-столбец

называется собственным вектором квадратной матрицы А n -го порядка, соответствующим собственному значению , если он удовлетворяет матричному уравнению

Здесь E – единичная матрица n -го порядка, а 0 – нулевой вектор-столбец. При условии, что вектор X 0, получаем характеристическое уравнение для определения собственных значений :

.

Координаты собственного вектора X_i соответствующего собственному значению , является решением системы уравнений

Собственный вектор определяется с точностью до постоянного множителя.

Пример 1. По координатам вершин пирамиды А ₁ А ₂ А ₃ А ₄найти: 1) длины ребер А ₁ А ₂и А ₁ А ₃; 2) угол между ребрами А ₁ А ₂и А ₁ А ₃; 3) площадь грани А ₁ А ₂ А ₃; 4) объем пирамиды. Если

А ₁(3;–2;2), А ₂(1;–3;1), А ₃(2;0;4), А ₄(6;–4;6).

Решение. 1) Находим векторы

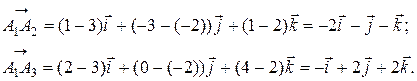
Длины этих векторов, т.е. длины ребер A₁A₂ и A₁A₃, таковы:

2) Находим скалярное произведение векторов , заданных в координатной форме:

а угол между векторами, находим как косинус угла между векторами

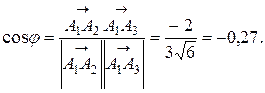
Отсюда следует, что – тупой угол, равный радиан с точностью до 0,01.

3) Площадь грани A ₁ A ₂ A ₃ равна половине площади параллелограмма, построенного на векторах , т.е. половине модуля векторного произведения этих векторов:

Здесь определитель вычисляется разложением по первой строке. Следовательно,

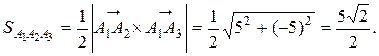
4) Объем V пирамиды равен 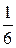объема параллелепипеда, построенного на векторах . Вектор . Используя формулу смешанного произведения векторов, получаем:

 

Пример 2. Найти угол между плоскостью Р ₁, проходящей через точки А₁(2;–4;1), А₂(–1;2;0), А₃(0;–2;3), и плоскостью Р ₂, заданной уравнением

Решение. Уравнение плоскости Р ₁ находим по формуле :

т.е.

По уравнениям плоскостей определяем их нормальные векторы: . Угол j между плоскостями Р ₁ и Р ₂ находим по формуле :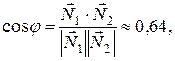

откуда

 

Пример 3. Составить уравнение прямой, проходящей через точки А ₁(4;–3;1) и А ₂(5;–3;0).

Решение. Используя формулу , получаем

Равенство нулю знаменателя второй дроби означает, что прямая принадлежит плоскости у = ­–3.

 

Пример 4. С помощью формул Крамера найти решение системы линейных уравнений

Решение. Вычислим определитель системы

Так как , то решение системы может быть найдено по формулам Крамера . Для этого найдем :

Подставляя найденные значения определителей в формулы, получаем искомое решение системы:

 

Пример 5. найти решение системы примера 4 с помощью обратной матрицы.

Решение. Здесь

Так как определитель матрицы системы отличен от нуля (см.пример 4): , то матрица А имеет обратную. Для нахождения обратной матрицы вычислим алгебраические дополнения элементов матрицы А:

Согласно формуле , матрица , обратная к А, имеет вид

.

Проверим правильность вычисления , исходя из определения обратной матрицы и используя формулу :

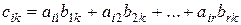Матричное решение системы в силу формулы имеет вид

откуда следует (из условия равенства двух матриц), что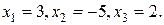

 

Пример 6. Найти решение однородной системы линейных уравнений

Решение. Однородная система имеет нетривиальное решение, если ранг матрицы системы

меньше числа неизвестных . Приведем матрицу А к каноническому виду А_r путем элементарных преобразований. Прибавляя к 1-му столбцу 3-й, а из 3-го вычитая 2-й, получаем

Умножим 1-й столбец на 1/4, а затем вычтем из 3-й строки 1-ю:

Из 3-й строки вычтем 2-ю, умноженную на 4, а затем ко 2-му и 3-му столбцам прибавим 1-й столбец, умноженный соответственно на 3 и 1:

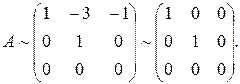
Таким образом, ранг матрицы А равен 2 и система имеет нетривиальное решение. Примем за главные неизвестные х ₁ и х ₂. Тогда система сводится к системе двух уравнений

решение которой имеет вид 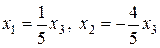. Придавая свободному неизвестному х ₃ произвольные значения , получаем решение системы в виде .

 

Пример 7. Определить собственные значения и собственные векторы матрицы .

Решение. Характеристическое уравнение для данной матрицы имеет вид :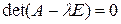

откуда следует, что матрица А имеет два собственных значения 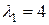и . Собственный вектор Х ₁, соответствующий 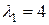, определяется из системы уравнений вида

которая сводится к одному уравнению . Полагая 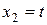, получаем решение в виде , 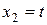. Следовательно, первый собственный вектор есть

Второй собственный вектор Х ₂, соответствующий собственному значению , определяется из системы уравнений вида

Эта система уравнений также сводится к одному уравнению ; полагая 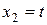, запишем ее решение в виде , 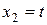. Следовательно, второй собственный вектор есть

Таким образом, матрица А имеет два собственных различных значени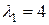й и и два собственных вектора, равных (с точностью до постоянного множителя) ,

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: