 |
Применение производных к исследованию свойств функций
|
|
|
|
Определение: Производной функции в точке х 0 называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
.
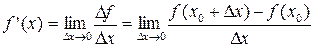Так как при 
имеем 
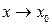, то определение производной можно записать в виде:
.
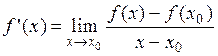При вычислении производной функции, необходимо помнить следующие правила дифференцирования:
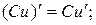
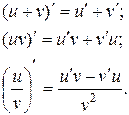
Сводная таблица формул дифференцирования
1. 
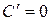
| 1.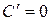
|
2. 
| 2.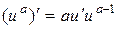 
|
3. 
| 3. 
|
4. 
| 4. 
|
5. 
| 5. 
|
6. 
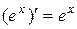
| 6.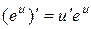 
|
7. 
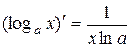
| 7.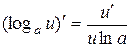 
|
8. 
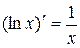
| 8.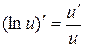 
|
9. 
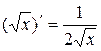
| 9.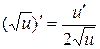 
|
10. 
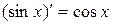
| 10.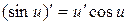 
|
11. 
| 11. 
|
12. 
| 12. 
|
13. 
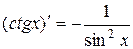
| 13. 
|
14. 
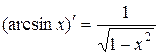
| 14.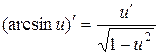 
|
15. 
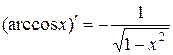
| 15.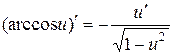 
|
16. 
| 16.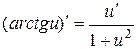 
|
17. 
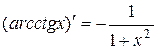
| 17. 
|
18. 
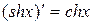
| 18.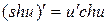 
|
19. 
| 19. 
|
20. 
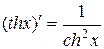
| 20.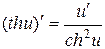 
|
21. 
| 21. 
|
Производная функции так же применяется при вычислении пределов функций. Правило ее применения сформулировано в следующей теореме.
Теорема (правило Лопиталя). Предел отношения двух бесконечно малых или бесконечно больших функций (неопределенность вида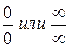 
) равен пределу отношения их производных:
если предел справа существует.
Пример 1. Используя правило Лопиталя, вычислить предел функции:
1) 
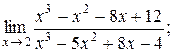2) 
Решение. 1) Подстановка предельного значения аргумента х = 2 приводит к неопределённости вида 0/0. Раскроем ее с помощью правила Лопиталя:
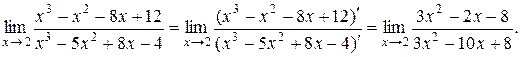
Однократное применение правила Лопиталя не приводит к раскрытию неопределенности (по прежнему получаем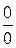 
), поэтому применим его еще раз:
Таким образом, в результате двукратного применения правила Лопиталя находим, что искомый предел равен 5.
2) Убедившись, что имеет место неопределенность вида 
, применим правило Лопиталя:
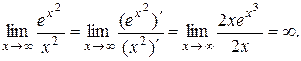
Применение производных к исследованию свойств функций
Определение. Если в некоторой окрестности точки x0 выполняется неравенство f(x) < f(x0) или f(x) > f(x0), то точка x0 называется точкой экстремума функции f(x) (соответственно точкой максимума или минимума).
|
|
|
Необходимое условие существования экстремума: если x0 экстремальная точка функции f(x), то первая производная 
равна либо нулю, либо бесконечности, либо не существует.
Достаточное условие существования экстремума: x0 является экстремальной точкой функции f(x), если ее первая производная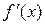 
меняет знак при переходе через точку x0: с плюса на минус – при максимуме, с минуса на плюс – при минимуме.
Определение. Точка x0 называется точкой перегиба кривой y = f(x), если при переходе через точку x0 меняется направление выпуклости.
Необходимое условие существования точки перегиба: если x0 точка перегиба кривой y = f(x), то вторая производная 
равна либо нулю, либо бесконечности, либо не существует.
Достаточное условие существования точки перегиба: x0 является точкой перегиба кривой y = f(x), если ее вторая производная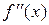 
меняет знак при переходе через точку x0.
Определение. Прямая y = kx + b называется наклонной асимптотой кривой y = f(x), если расстояние от точки (x;f(x)) кривой до этой прямой стремится к нулю при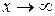 
.
При этом
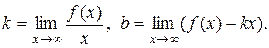
При k = 0 имеем горизонтальную асимптоту: y = b.
Если
то прямая x = a называется вертикальной асимптотой.
Общая схема исследования функции и построения ее графика
I. Элементарное исследование:
1) найти область определения функции;
2) исследовать функцию на симметричность и периодичность;
3) вычислить предельные значения функции в ее граничных точках;
4) выяснить существование асимптот;
5) определить, если это не вызовет больших затруднений, точки пересечения графика функции с координатными осями;
6) сделать эскиз графика функции, используя полученные результаты.
II. Исследование графика функции по первой производной:
1) найти решения уравнений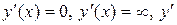 
не существует;
2) точки, «подозрительные» на экстремум, исследовать с помощью достаточного условия экстремума, определить вид экстремума;
|
|
|
3) вычислить значения функции в точках экстремума;
4) найти интервалы монотонности функции;
5) нанесите на эскиз графика экстремальные точки;
6) уточнить вид графика функции согласно полученным результатам.
III. Исследование графика функции по второй производной:
1) найти решения уравнений 
не существует;
2) точки, «подозрительные» на перегиб, исследовать с помощью достаточного условия;
3) вычислить значения функции в точках перегиба;
4) найти интервалы выпуклости и вогнутости графика функции;
5) нанесите на эскиз графика точки перегиба;
6) окончательно построить график функции.
Если исследование проведено без ошибок, то результаты всех этапов должны согласоваться друг с другом. Если же согласование отсутствует, необходимо проверить правильность результатов отдельных этапов и исправить найденные ошибки.
Пример 1. Исследовать на экстремум функцию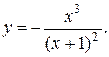 
Решение. Находим первую производную: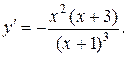 
Из уравнени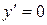й 
и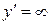 
получаем точки, «подозрительные» на экстремум: 
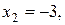
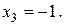Исследуем их, определяя знак первой производной слева и справа от каждой точки. Для наглядности результаты представим в виде таблицы изменения знака 
:
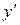| х | (–¥, –3) | –3 | (–3, –1) | –1 | (–1, 0) | (0, +¥) | |
|
| – | + | ¥ | – | – | ||
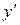
| у | убыв. | min | возр. | не опр. | убыв. | убыв. |
В первой строке указаны интервалы, на которые область определения функции разбивается точками х 1, х 2, х 3, и сами эти точки. Во второй строке указаны знаки производной 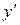в интервалах монотонности. В третьей строке приведено заключение о поведении функции.
Исследуемая функция, как следует из таблицы, имеет минимум в точке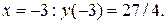 
Точки х = –1 и х = 0 не являются точками экстремума, так как в первой точке функция не определена, а в окрестности второй точки первая производная сохраняет знак.
Пример 2. Найти асимптоты графика функции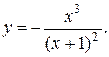
Решение. Точка х = –1 является точкой разрыва функции. Так как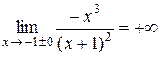 
, то прямая х = –1 служит вертикальной асимптотой графика функции.
Ищем наклонные асимптоты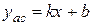 
, используя формулы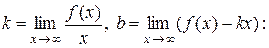 
Таким образом, уравнение наклонной асимптоты имеет вид 
.
Пример 3. Построить график функции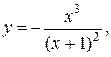 
используя общую схему исследования функции.
Решение. I. Область определения: (–¥, –1), (–1; +¥). Функция не является симметричной и периодической. Находим предельные значения функции:
|
|
|
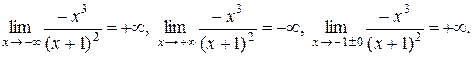
График функции имеет одну вертикальную асимптоту х = –1 и одну наклонную асимптоту 
(см. пример 3.4.). Он пересекает координатные оси в точке (0; 0).
II. Функция имеет один минимум при х = –3. (см. пример 3.3.).
III. Вторая производная 
обращается в бесконечность при х = –1 и равна нулю в точке х = 0, которая является единственной точкой перегиба (см. таблицу):
| х | (–¥, –1) | –1 | (–1, 0) | (0, +¥) | |
| + | ¥ | + | – | |
| у | È | не опр. | È | точка перегиба | Ç |
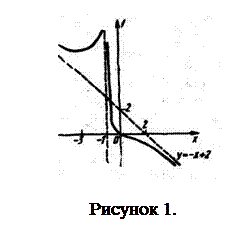Учитывая полученные результаты, строим график функции 
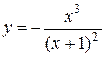(рисунок 1).
Пример 4. Найти первую производную функции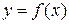 
, заданной параметрически: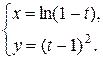 
Решение. Дифференцируем х (t) и y (t) по параметру t: 
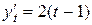. Искомая производная от у по х равна отношению производных от y (t) и от x (t) по t:
|
|
|
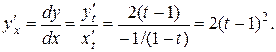
