 |
Введение в математический анализ
|
|
|
|
Определение. Функция f(x) (F(x)) называется бесконечно малой (бесконечно большой) при x 
, если 
.
Определение. Две функции f(x) и 
, одновременно стремящиеся к нулю или бесконечности при x , называются эквивалентными, если
.
Предел отношения бесконечно малых (бесконечно больших) функций не изменится, если каждую из них заменить эквивалентной ей функцией, т.е.
,
если f(x)~f1(x), 
~ 
.
При решении задач удобно помнить следующие формулы:
Определение: Предел элементарной функции в точке области ее определения равен частному значению этой функции в этой точке:
Нарушение ограничений, накладываемые на функции при вычислении их пределов, приводит к неопределенностям вида:
.
Для каждого вида неопределенности существует свое правило раскрытия.
Для раскрытия неопределенности вида 
, нужно числитель и знаменатель дроби разделить на высшую степень переменной или взять отношение коэффициентов при высшей степени переменной.
Для раскрытия неопределенности вида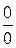 
необходимо выполнить действия, приводящие к сокращению на множитель, создающий неопределенность. Если же дробь содержит не сократимые между собой функции, то необходимо прибегнуть к формулам замены эквивалентных бесконечно малых функций.
Неопределенность вида 
раскрывается с помощью второго замечательного предела.
Остальные виды неопределенностей приводятся к рассмотренным выше, а затем применяется необходимое правило.
I замечательный предел: 
.
II замечательный предел: 
Отметим также, что
Определение. Функция f(x) называется непрерывной в точке x = a, если:
1) частное значение функции в точке x = a равно f(a);
2) существуют конечные односторонние пределы функции
3) односторонние пределы равны:
|
|
|
4) предельное значение функции в точке x=a равно ее частному значению f(a):
C = f(a).
Обозначение: 
.
Определение. Точка x = a называется точкой устранимого разрыва, если f(a) 
.
Определение. Точка x = a называется точкой разрыва I рода, если оба односторонних предела конечны, но 
.
Определение. Точка x = a называется точкой разрыва II рода, если хотя бы один из односторонних пределов равен бесконечности или не существует.
Пример 1. Найти 
.
Решение. Подставляя вместо х его предельное значение, равное 3, получаем в числителе бесконечно большую, а в знаменателе – бесконечно малую функцию:
Поэтому 
.
Пример 2. Найти 
.
Решение. Подстановка предельного значения аргумента приводит к неопределенности вида 
. Так как под знаком предела стоит отношение двух многочленов, то разделим числитель и знаменатель на старшую степень аргумента, т.е. х 4. В результате получим
поскольку при 
функции 
и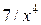 
являются бесконечно малыми.
Пример 3. Найти 
.
Решение. Для раскрытия получающейся здесь неопределенности вида 0/0 используем метод замены бесконечно малых эквивалентными. Так как 
при 
, то
Пример 4. Найти 
.
Решение. Подстановка 
приводит к неопределенности . Произведем замену переменных: 
, 
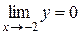. Тогда
Пример 5. Исследовать функцию 
на непрерывность; найти точки разрыва функции и определить их тип. Построить схематический график функции.
Решение. Так как данная функция определена на всей числовой оси, то «подозрительными на разрыв» являются те точки, в которых изменяется аналитическое выражение функции, т.е. 
и 
. Вычислим односторонние пределы в этих точках.
Для точки имеем:
Односторонние пределы функции в точке существуют, но не равны между собой. Следовательно, эта точка является точкой разрыва первого рода.
Для точки получаем
Односторонние пределы функции при равны между собой и равны частному значению функции: 
Следовательно, исследуемая точка является точкой непрерывности.
|
|
|
График данной функции приведен на рисунке 7.
|
|
|
