Главная | Обратная связь | Поможем написать вашу работу!

Лабораторная работа № 2. Организация вычислительного процесса при решении задачи распознавания графического образа

СИСТЕМЫ РАСПОЗНАВАНИЯ ОБРАЗОВ

Рекомендовано к изданию Редакционно-издательским советом

федерального государственного бюджетного образовательного учреждения

высшего профессионального образования

«Оренбургский государственный университет»

в качестве методических указаний для студентов, обучающихся по программам высшего профессионального образования по направлению подготовки

090900.62 Информационная безопасность

Оренбург

2012

УДК 681.3(075)

ББК 32.973.2-02я7

А 79

Рецензент- кандидат технических наук, доцент А.В. Хлуденев

Аралбаев, Т.З.

А 79 Системы распознавания образов: методические указания к лабораторным работам / Т.З. Аралбаев, А.Ю. Кручинин, Р.И. Хасанов; Оренбургский гос. ун-т. – Оренбург: ОГУ, 2012. – 64 с.

Лабораторный курс содержит 8 лабораторных работ и методические указания к ним. Каждая работа включает теоретическое изложение материала, постановку задачи, порядок выполнения и контрольные вопросы для самоподготовки.

Лабораторный курс рекомендован преподавателям, как вспомогательный материал в организации и проведении занятий, а также студентам, обучающимся по специальности и профилю «Комплексная защита объектов информатизации» для аудиторного и самостоятельного освоения лабораторного курса дисциплины «Системы распознавания образов».

УДК 681.3(075)

ББК 32.973.2-02я7

Хасанов Р.И., 2012

. Содержание

Обозначения и сокращения………………………………………………..……….	4
Введение………………………………………………………..................................	5
1 Лабораторная работа № 1. Классификация периодов солнечной активности	6
2 Лабораторная работа № 2. Организация вычислительного процесса при решении задачи распознавания графического образа………………………………	10
3 Лабораторная работа № 3. Распознавание контуров геометрических объектов на графических изображениях………………………………………………..	19
4 Лабораторная работа № 4. Технологии распознавания двумерных штрих-кодов………………………………………………………………………………….	28
5 Лабораторная работа № 5. Распознавание текста в графическом изображении……………………………………………………………………………………	39
6 Лабораторная работа № 6. Ситуационный принцип в задаче распознавания образов……………………………………………………………………………….	48
7 Лабораторная работа № 7. Ассоциативно-мажоритарная модель распознавания образов…………………………………………………………………………..	55
8 Лабораторная работа № 8. Генетический алгоритм распознавания образов…………………………………………………………………………………….	60
9 Литература, рекомендуемая для изучения тем……………………………….....	66

Обозначения и сокращения

БПФ – быстрое преобразование Фурье;

ГА – генетический алгоритм;

ГО – графический образ;

ДП – дорожное полотно автомобильной дороги;

ЗУ – запоминающее устройство;

ИП – информативный признак;

ППР – правило принятия решения;

РФ – разделяющая функция;

РП – разделяющее правило;

СА – солнечная активность;

СГ – сетевой график;

СПО – система параметрической оптимизации;

СРО – система распознавания образов;

УРО – устройство распознавания образов.

Введение

Настоящий лабораторный практикум предназначен для получения практических навыков студентами специальности и профиля подготовки – «Комплексная защита объектов информатизации» при изучении дисциплины «Системы распознавания образов» (СРО).

Лабораторный курс содержит восемь работ, рассчитанных на 36 часов аудиторных занятий. Предлагаемые задания охватывают основные разделы рабочей программы, связанные с изучением технологии и организации проектирования систем распознавания образов.

Общие методические рекомендации по использованию лабораторных работ и методических указаний:

- к выполнению лабораторной работы следует приступать после ознакомления с теоретической частью соответствующего раздела и рекомендациями, приведенными в конкретной работе;

- лабораторные работы рекомендуется выполнять в порядке их нумерации в аудиторное время, указанное в описании работы;

- рекомендуется для экономии времени отчеты о лабораторных работах оформлять в виде протоколов работы с обязательным указанием даты, номера, темы, цели работы и выводов с краткой характеристикой результата;

- дополнительные сведения по лабораторным работам содержатся в прилагаемом списке литературы.

Лабораторный курс может быть освоен на индивидуальном компьютере со средними техническими характеристиками. Обязательным для полной реализации курса является наличие комплекта офисных приложений и объектно-ориентированной среды программирования Delphi, желательно иметь выход в Интернет.

Практикум рекомендован преподавателям как вспомогательный материал в организации и проведении занятий, а также студентам – для аудиторного и самостоятельного освоения лабораторной части дисциплины СРО.

Лабораторная работа № 1. Классификация периодов солнечной активности

Цель работы: построить экспериментальную классификацию периодов солнечной активности (СА) на основе исследования и кодирования параметров спектров

Теоретическая часть

Исследование солнечной активности относится к перечню задач, которым длительное время уделяют внимание специалисты из разных областей науки. Предметом исследования являются данные временных рядов, так называемые числа Вольфа, регистрация которых известна с 1700 года по настоящее время. Цель проводимых исследований - выявление влияния солнечной активности на целый ряд земных процессов, например: эпидемии болезней, урожайность сельскохозяйственных культур, стихийные бедствия, изменения в обществе и другие. В настоящей и последующей работе рассматриваются вопросы начального изучения этой проблемы.

Систематизацией наблюдений за солнечными пятнами впервые занялся цюрихский астроном Р. Вольф. Им, в частности, предложена следующая формула для ежемесячной оценки солнечной активности:

(1.1)

где W – число Вольфа; g – число групп и отдельных пятен на Солнце; f – число пятен в группах и отдельно; k – поправочный коэффициент, учитывающий характеристики измерительных приборов.

На сайте WWW.astronom2000.info/астрономия/солнечная активность представлены ежемесячные наблюдения значений чисел Вольфа, начиная с 1749 года. Известно, что периодичность изменения солнечной активности близка к 11,2 года и составляет 134 месяца.

Классификация периодов СА необходима для упорядочивания и систематизации множества периодов солнечной активности в процессе ее исследования. Классификация является результатом кластерного анализа периодов солнечной активности, в котором выявляются общие и отличительные признаки спектров солнечной активности для объединения периодов в отдельные группы.

В кластерном анализе обычно выполняются следующие операции:

а) отбор выборки для анализа и классификации;

б) определение признаков классификации;

в) определение меры сходства между объектами;

г) построение собственно классификации;

д) проверка классификации.

Согласно пункту «а» по данным источника [9] в распоряжении исследователя имеются данные по периодам солнечной активности с 1749 по 2009 год.

В общем случае исследование СА преследует различные цели, причем изучается как спектр сигналов целиком, так и его отдельные гармоники. Перечень гармоник определяется условиями задачи. В настоящей работе, учитывая лишь ее учебно-познавательную значимость, а так же специфику применения БПФ в системе MathCAD, принимаются следующие допущения:

- перечень гармоник выбирается произвольно, например, с периодами три, четыре, шесть и двенадцать месяцев;

- при расчете спектров использовать данные за первые 128 месяцев каждого периода, т.е. данные усечены на 6 замеров.

Определение признаков классификации является отдельной задачей. Учитывая учебный характер настоящей работы, выбор их производится произвольно, т.е. для классификации периодов СА используем гармоники с периодами 3, 4, 6 и 12 месяцев, т.е. число признаков i = 4.

Меру сходства между периодами солнечной активности определим по величинам кодов K_n, соответствующих спектрам N периодов СА (n = 1.. N).

Код K_n определяется по следующим выражениям:

	(1.1)
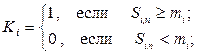
	(1.2)
	(1.3)

где S_i _{, n} – амплитудная оценка для i -ой гармоники (из числа выбранных) в n -ом периоде СА; m_i – среднее значение амплитудных оценок спектра для i -ой гармоники по всем исследуемым спектрам СА.

Таким образом, число j определяет максимально возможное число классов, на которое можно разбить исходную выборку периодов СА. Построение классификаций периодов производится объединением в группы периодов с одинаковыми кодами.

Построенная классификация проверяется на соответствие числа разбиваемых на классы периодов сумме периодов, охваченных всеми классами, а так же на непревышение общего числа классов величины 2 ^j.

Порядок выполнения работы

1. Создайте документ MathCad. Прочитайте данные о СА в вектор U. Перечень исследуемых периодов СА и файл с данными предоставляется преподавателем или формируется студентом по данным источника [9].

Вариант документа представлен на рисунке 1.1.

Рисунок 1.1 – Вычисление амплитудных оценок для исследуемых гармоник

по периодам СА

2. Рассчитать спектральные оценки СА по заданным периодам (например, для N последовательно чередующихся периодов) для гармоник, соответствующих 3, 4, 6 и 12 месяцам.

3. Построить по N точкам графики изменения амплитудных оценок гармоник с периодами 3, 4, 6 и 12 месяцев.

4. Рассчитайте среднее значение амплитудных оценок спектра для каждой выбранной гармоники по N периодам по формуле (1.3).

5. Вычислите классификационные признаки K по N периодам согласно формуле (1.2).

Возможный вариант документа MathCad для N=24 представлен на рисунке 1.2.

Рисунок 1.2 – Вычисление элементов классификационного кода периода СА

6. Произведите классификацию периодов СА, используя значения классификационных признаков K. Периоды солнечной активности относятся к одному классу, если их классификационные коды полностью совпадают.

7. Сделайте выводы по работе и составьте отчет. В отчете должны быть представлены значения классификационных кодов каждого периода СА.

1.4 Контрольные вопросы

1. Порядок вычисления классификационного кода периода СА.

2. Как может быть использована на практике классификация периодов СА?

3. Как определить максимально возможное число классов по данной классификации?

4. Перечислите операции кластерного анализа.

5. Объясните понятие «корреляция данных».

Лабораторная работа № 2. Организация вычислительного процесса при решении задачи распознавания графического образа

Цель работы: освоить способ распараллеливания вычислительного процесса на примере задачи распознавания графического образа

Теоретическая часть

Эталонный графический образ (ГО) X представляется в формате BMP матрицей пикселов размером M столбцов на N строк. Исследуемый графический образ Y является частью образа X, представляется в аналогичном формате и имеет размеры n * m. Образ Y может быть зашумлен цветовыми помехами для исследования параметров распознавания. Процент зашумления (искажения) пикселов находится в диапазоне от 0 до 50%.

Суть задачи распознавания заключается в определении места положения фрагмента образа Y на исходном образе в условиях зашумления изображения фрагмента. Решение данной задачи в условиях больших размеров графических образов и значительной степени зашумления предоставляет для исследователя определенные сложности.

На рисунке 2.1 в качестве примера представлена постановки и решения задачи идентификации места положения фрагмента среза головного мозга при исследовании его с помощью томографа. На рисунке 2.1 в пунктах “а” и “б” представлены соответственно образы X и Y, в пункте “в” – график коэффициента парной корреляции цветовых характеристик образов X и Y при скольжении образа Y по поверхности образа X слева на право.

Для формализации задачи распознавания введем следующие условные обозначения: Q_Y – образ фрагмента; Q ={ q ₁, q ₂, …, q_R } – множество вариантов образов основного образа; P = { p ₁, p ₂, p ₃ } – множество признаков распознавания; RF = K_XY (P_X, P_Y) – разделяющая функция; RP – разделяющее правило.

Число вариантов образов R при скольжении фрагмента образа по основному образу с шагом Δ M:

(2.1)

Число признаков распознания соответствует числу основных цветов в цветовой модели графического образа RGB, т.е. – трем.

В качестве разделяющей функции при распознавании места положения образа Y выбрана функция коэффициента парной корреляции R_XY:

	(2.2)		(2.3)
	(2.4)		(2.5)

где K_xy – коэффициент ковариации; x_i и y_i – соответственно текущие значения интенсивностей цвета по выборке; 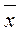и – соответственно, оценки средних значений интенсивностей цвета по выборке; L – число элементов выборке; и 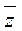– соответственно текущие значения интенсивностей некоторого цвета и оценки среднего по выборке (i = 1, L); σ – среднее квадратическое отклонение по выборке.

Порядок выполнения работы

На рисунке 2.1 представлена общая схема корреляционного метода для решения задачи.

Разделяющее правило для определения соответствия образа фрагмента Q_Y одному из вариантов образов основного образа Q выглядит следующим образом:

(2.6)

т.е. отнесение образа Q_y к одному из вариантов Q^* образов Q осуществляется по максимальной близости признаков образов.

Рисунок 2.1 – Общая схема корреляционного метода решения задачи

На рисунке 2.2 представлена схема построения пространственных рядов признаков образов Q_Y и Q_X.

Рисунок 2.2 – Схема построения графиков интенсивностей цветов модели RGB

графических образов

В частности, в пункте “а” представлен порядок формирования пространственных рядов интенсивностей цвета: красного (I_R), зеленого (I_G) и синего (I_B) – по трем столбцам матрицы пикселов. Общее число столбцов соответствует числам M и m для исследуемых образов. В пункте “б” рисунка 2.2 представлены графики изменения интенсивности цветов для сравниваемых образов.

Расчет параметров по формулам (2.1) – (2.5) производится на данных пространственных рядов, представленных на рисунке 2.2 “б”, где N – число элементов пространственного ряда.

На рисунке 2.3 представлен общий вид демонстрационной программы идентификации места положения фрагмента Q_Y на поверхности образа Q_X.

Как видно из рисунка 2.3, распознавание места положения фрагмента проведено по интенсивности зеленого цвета с уровнем зашумления в 10%. При этом R_maxXY = 0.896, номера начального и конечного столбца пикселов образа Q_X, соответствующие фрагменту, имеют значения, соответственно, 105 и 135.

Рисунок 3.3 – Общий вид программы идентификации местоположения фрагмента

Анализ математического описания задачи и работы демонстрационной программы позволил сделать следующие выводы, которые необходимо учесть при решении задачи организации вычислительного процесса:

1. Задача распознавания графического образа представляет собой сложный вычислительный процесс;

2. Сложность вычислительного процесса обусловлена:

- размерами графических образов Q_X и Q_Y;

- большой мощностью множества Q;

- необходимостью идентификации по трем цветовым признакам R, G и B;

- большим объемом вычислений статистических оценок по выражениям (2.2) – (2.6).

3. Для эффективного решения задачи распознавания графического образа в условиях реального времени необходимо распараллеливание процесса обработки данных.

4. В качестве основных аспектов распараллеливания процесса рекомендуется использовать параллельную обработку данных: по цветовым признакам модели RGB, по зонам поиска, число которых вычисляется по формуле (2.1), по вычислению выражений (2.2) – (2.6).

Одним из методов организации параллельных процессов рекомендован метод сетевого планирования [6], предусматривающий выполнение следующих основных операций:

- определение всего перечня вычислительных операций, выполняемых при решении задачи;

- определение перечня операций, выполняемых параллельно и последовательно;

- построение сетевого графика (СГ);

- расчет элементов СГ и его оптимизация.

На рисунке 2.4 представлен вариант СГ некоторого вычислительного процесса.

Рисунок 2.4 – Пример сетевого графика вычислительного процесса

Вершинами СГ являются события, соответствующие выполнению операций по обработке данных. Ребра СГ характеризуют направления вычислительного процесса, также время (на рисунке 2.4 показано над стрелками) и число процессоров, отведенных для каждой операции (p 1 – p 12).

События характеризуются началом и завершением вычислительной операции. Любая последовательность операций в СГ называется путем L. Продолжительность (длина) пути T (L) равна сумме продолжительности составляющих его операций. Путь, имеющий наибольшую продолжительность T_кр, называется критическим.

В таблице 2.1 приведены характеристики путей СГ, представленного на рисунке 2.4.

Таблица 2.1 – Характеристики маршрутов сетевого графика

№ п/п	*L_n*	*T (L_n)*	№ п/п	*L_n*	*T (L_n)*
1	1 – 2 – 6 – 7	8	6	1 – 3 – 5 – 7	17
2	1 – 2 – 5 – 7	13	7	1 – 2 – 3 – 5 – 7	18
3	1 – 2 – 5 – 6 – 7	10	8	1 – 4 – 7	16
4	1 – 2 – 3 – 5 – 6 – 7	15	9	1 – 4 – 5 – 6 – 7	11
5	1 – 3 – 5 – 6 – 7	14	10	1 – 4 – 5 – 7	14

Ранний и поздний сроки свершения конкретного i -го события t_p (i) и t_п (i) определяются по максимальному из путей, проходящих через это событие, причем t_p (i) равно продолжительности максимального из предшествующих событию путей; t_п (i) равно разности между T_кр и продолжительностью максимального из последующих за событием путей. Резерв времени для некоторого события характеризует запас времени, на который можно сдвинуть сроки свершения других событий. Он равен разности между t_п (i) и t_p (i). События критического пути резерва времени не имеют.

На рисунке 2.5 представлена временная диаграмма событий сетевого графика по рисунку 2.4 с распределением процессоров по операциям.

Рисунок 2.5 – Временная диаграмма событий сетевого графика с распределением процессов по операциям

Общее число процессоров, выделенных для реализации вычислительного процесса равно 10. Цифра над горизонтальными линиями соответствуют участкам СГ. Цифры под горизонтальными линиями соответствуют количеству процессоров, выделенных для выполнения конкретной операции. Общее число процессоров, находящихся в работе в каждый момент времени, не должно превышать 10.

12 3 4 5 6 7 Следующая ⇒

Воспользуйтесь поиском по сайту: