 |
Задание на лабораторную работу
|
|
|
|
1. Написать программу, распознающую символы по методу шаблонов. В качестве эталонных символов использовать символы из соответствующего варианта (таблица 5.1), шаблонный метод по варианту. При обучении на вход программы должны поступать BMP-файлы, в каждом из которых находится по одному символу. При тестировании на вход программы поступает BMP-файл, а программа выдает результат – распознанный символ.
2. Тестирование должно проводиться по следующим выборкам (наборам BMP файлов):
а) эталонная;
б) эталонная, но с изменением масштабов;
в) те же символы, но набранные другим шрифтом;
г) наклоненные вглубь символы (например, с помощью Paint: рисунок → растянуть → наклон → по горизонтали);
д) случайным образом зашумленные (некоторое количество разноцветных точек на изображении).
3. Проанализировать полученные результаты, построив таблицы результатов распознавания для каждого варианта тестирования.
Варианты заданий
Варианты заданий для выполнения лабораторной работы представлены в таблице 5.1.
Таблица 5.1 – Варианты заданий для выполнения лабораторной работы №5
| Номер варианта | Символы | Тип шаблона (рисунок 5.5) | Шрифт | Размер шаблона (X × Y) |
| 1 | Q, W, E, R, T, Y | А | Arial | 5 × 7 |
| 2 | U, I, O, P, A, S | Б | Times | 10 × 10 |
| 3 | D, F, G, H, J, K | П | Verdana | 10 × 14 |
| 4 | L, Z, X, C, V, B | Б | Cambria | 6 × 10 |
| 5 | N, M, 1, 2, 3, 4 | А | Courier | 5 × 10 |
| 6 | 5, 6, 7, 8, 9, 0 | Б | Tahoma | 12 × 12 |
| 7 | Ц, У, К, Е, Н, Г | А | Impact | 5 × 7 |
| 8 | Ш, Щ, З, Х, Ъ, Ф | Б | Arial | 10 × 10 |
| 9 | Ы, В, А, П, Р, О | А | Times | 10 × 14 |
| 10 | Л, Д, Ж, Э, Я, В | Б | Verdana | 6 × 10 |
| 11 | С, М, И, Т, Ь, Б | А | Cambria | 5 × 10 |
| 12 | 1, 2, 3, 4, 5, 6 | Б | Courier | 12 × 12 |
| 13 | A, B, C, D, E, F | А | Tahoma | 5 × 7 |
| 14 | I, J, K, L, M, N | Б | Impact | 10 × 10 |
| 15 | O, P, R, S, T, Q | А | Arial | 10 × 14 |
| 16 | X, Y, Z, 0, 1, 2 | Б | Times | 6 × 10 |
| 17 | А, Е, И, О, У, Ю | А | Verdana | 5 × 10 |
| 18 | А, Б, В, Г, Д, Е, Ж | Б | Cambria | 12 × 12 |
| 19 | З, И, К, Л, М, Н | А | Courier | 5 × 7 |
| 20 | О, П, Р, С, Т, У | Б | Tahoma | 10 × 10 |
|
|
|
5.5 Контрольные вопросы
1. Что такое бинаризация?
2. Чем отличается пороговая бинаризация от адаптивной бинаризации?
3. В чем суть шаблонного метода распознавания символов?
4. Какие методы оптимального определения порогового значения бинаризации вы знаете?
5. Какие помехи накладываются на реальные символы?
Лабораторная работа № 6. Ситуационный принцип в задаче распознавания образов
Цель работы: освоить принципы построения системы ситуационного распознавания образов
Теоретическая часть
Подход «ситуация управляет системой» закономерно возник в экономической отрасли, как инструмент оперативного контроля и управления экономическими субъектами в условиях быстроменяющихся финансовых ситуаций. Возможность применения данного подхода не ограничивается только социально-экономическими системами, например, ситуационное управление используется в поисковой системе Google, в менеджменте персонала, при управлении сложными техническими, эргатическими и организационными системами. Сложность задачи ситуационного управления распознаванием образов заключается в сравнительной оценке большого количества признаков (от нескольких десятков – до нескольких сотен) для выбора наиболее вероятных под лидирующие классы образов [7].
Модель системы распознавания образов имеет следующий вид: «значения признаков → ассоциативные оценки мер близости → коды сигнатур образов → коды ситуаций → оптимальные признаки».
Для формализации задачи использованы следующие условные обозначения [1, 7]: qx – неизвестный образ, подлежащий распознаванию; Q * – класс образов, к которому отнесен qx; < si > – зарегистрированное значение i -го признака, i = 1, m; < Sx > – вектор зарегистрированных значений признаков qx; V { qx, Qj } – мера близости между qx и j -ым образом из множества эталонов Q; vij {< si >, Qj } – частный параметр оценки ассоциативности значения < si > признака si из множества S для всех классов образов из Q, j = 1, n; Ф{< Sx >, Qj } – функционал для вычисления меры близости V { qx, Qj }; P (s) – множество функций оценок распределений значений признаков из S для всех классов образов Q; wij { vij, Qj } – коэффициент сигнатуры значения vij для j -го образа из множества эталонов Q; W { qx, Qj } – совокупность коэффициентов сигнатур, характеризующих ситуацию распознавания j -го образа из множества эталонов Q; Ф{ qx, si } – функционал для нахождения оптимальных (наиболее вероятных) признаков si из множества S для образа qx, исходя из ситуации распознавания; Rj – сумма попаданий < si > для i -го признака j -го класса образов.
|
|
|
В общем случае в теории и практике ситуационного управления распознаванием образов в качестве правил отбора образов из множества Q могут быть использованы:
- доминирующий стиль (выбор оптимальных признаков только для одного лидера, набравшего максимальное количество баллов);
- тандемный стиль (выбор оптимальных признаков для двух лидеров);
- командный стиль (лояльный выбор оптимальных признаков сразу для нескольких классов образов, лидирующих в “эстафете” распознавания Qj).
По способу выбора признаков в алгоритме существуют следующие:
- рулеточный (кольцевой перебор признаков si из множества S);
- вероятностный (выбор оптимальных признаков с учетом их рейтингов, исходя из вероятностей появления лидирующих образов).
Математическая модель распознавания qx имеет следующий вид [1, 7]:
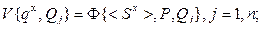
| (6.1) |
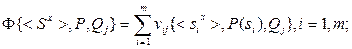
| (6.2) |
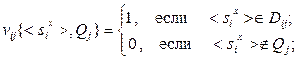
| (6.3) |

| (6.4) |

| (6.5) |
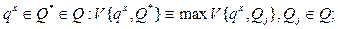
| (6.6) |

| (6.7) |

| (6.8) |
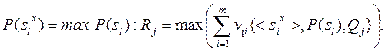
| (6.9) |
В матрице (6.5) каждый столбец соответствует частным мерам близости vij множества < Sx > для каждого класса образов по всем признакам. Сумма элементов каждой строки соответствует сумме в выражении (6.2). Выражение (6.6) описывает разделяющее правило, при котором отнесение qx к одному из классов образов-эталонов Q * производится на основе сигнатурного подхода и по максимальной величине меры близости, соответствующей сумме элементов в каждой строке матрицы (6.5). При обучении модели производится вычисление элементов матрицы (6.5) по выражениям (6.1) – (6.9).
|
|
|
Процесс распознавания qx сводится к вычислению суммы элементов матрицы по каждой строке, соответствующих < sx > и < Sx >, и выбору искомого класса образа по максимальной сумме. Принятие решения по максимальной сумме элементов строки матрицы с учетом сигнатурного подхода позволяет реализовать мажоритарный принцип и повышает достоверность распознавания образов. Достоинством представленной модели распознавания образов является высокая производительность, обусловленная простотой алгоритма вычисления разделяющей функции и реализации разделяющего правила. Аппаратная и программная реализация алгоритма на порядок проще и быстрее аналогичного алгоритма распознавания, работающего, например, по методу Байеса.
На рисунке 6.1 представлена схема алгоритма выбора оптимальных (наиболее вероятных) признаков среди множества S для лидирующих образов Q * на основе ситуационного принципа.
Входными данными алгоритма является: множество лидирующих классов образов Q * и множество неопрошенных признаков S Y. Выходными – матрица оптимальных признаков S P в порядке убывания приоритетов для лидирующих классов образов Q *.

Рисунок 6.1 – Схема алгоритма выбора оптимальных признаков
В ходе работы алгоритма осуществляется формирование двумерного динамического массива, представленного в таблице 6.1, в ячейки (столбцы № 2 – 4) которого записываются вероятности P (Qj *) появления j -го лидирующего образа для i -го неопрошенного признака Si Y. В пятый столбец массива записывается сумма вероятностей P (Q *) для i -го неопрошенного признака Si Y. После заполнения матрицы осуществляется поиск максимальной вероятности max P (Qj *) появления j -го лидирующего образа для i -го неопрошенного признака Si Y.
Таблица 6.1 – Пример динамического массива, содержащего вероятности P (Qj *) появления j -го лидирующего образа для i -го признака Si Y
| Код признака | P (Q 1*) | P (Q 2*) | P (Q 4*) | S P (Q *) | D1 = max P (Qj *) – P (Q 1*) | D2 = max P (Qj *) – P (Q 2*) | D4 = max P (Qj *) – P (Q 4*) | Значение приоритета |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| A | 5/20 | 6/20 | 4/20 | 15/20 | 1/20 | 0 | 2/20 | 0,6 |
| B | 7/20 | 4/20 | 1/20 | 12/20 | 0 | 3/20 | 6/20 | 0,15 |
| C | 3/20 | 1/20 | 4/20 | 8/20 | 1/20 | 3/20 | 0 | 0,20 |
| D | 8/20 | 0/20 | 3/20 | 11/20 | 0 | 8/20 | 5/20 | -0,1 |
|
|
|
Темным цветом в таблице 6.1 выделены вероятности P (Q *), которые являются максимальными max P (Qj *).
Далее формируются вектора (см. таблицу 6.1, столбцы № 6 – 8), содержащие разницу D между max P (Qj *) и остальными P (Q *). Полученные D последовательно вычитаются из S P (Q *) и формируют значение приоритета (см. таблицу 6.1, столбец №9). После вычисления значений приоритетов для всех неопрошенных признаков Si Y, массив сортируется по убыванию. На выходе алгоритма (см. рисунок 6.1) содержится список наиболее вероятных кодов признаков Si P в порядке убывания приоритетов.
Далее алгоритм программы осуществляет опрос соответствующего признака, который получил наибольшее значение приоритета. В режиме идентификации на адресные входы ассоциативного ЗУ последовательно поступают значения признаков исследуемого образа. В подсистеме принятия решений передаются меры близости vij множества < Sx > для каждого класса образов по всем признакам. На основании этих данных в подсистеме принятия решений формируется совокупность коэффициентов сигнатур W { qx, Qj }, характеризующих ситуацию распознавания j -го образа из множества эталонов Q. Через функционал Ф{ qx, si } алгоритм программы определяет оптимальные (наиболее вероятные) коды признаков si из множества S для лидирующих образов, исходя из ситуации распознавания.
Эффективность ситуационного алгоритма распознавания графических образов в среднем выполняется за три шага (итерации), тогда как для сигнатурного или классического ассоциативно-мажоритарного подхода требуется 5 – 6 итераций.
Таким образом, сигнатурный и ситуационный подходы позволяют оценить ситуацию по совокупности кодов сигнатур для выбора наиболее вероятных признаков под лидирующие классы образов и повысить оперативность принятия решения по распознаваемому классу образов.
Порядок выполнения работы
1. Запустить программу «Эмулятор системы ситуационного распознавания образов».
2. Используя теоретический материал, представленный в пункте 6.1, разобраться в ситуационном и сигнатурном принципах в задаче распознавания образов.
3. Изучить представленный программный эмулятор:
- режим настройки объема ассоциативного ЗУ;
- режим распознавания образов в соответствии с вариантом задания;
- режим пост обработки журнала вычислительного эксперимента.
4. В процессе работы эмулятора пользователь должен определить достоинства сигнатурного и ситуационного подходов, которые следует указать в отчете о проделанной работе.
|
|
|
|
|
|


