 |
Тема 1. Изучение нормального закона распределения.
|
|
|
|
Л.А. ШАПИРО, Н.Г. ШИЛИНА
РУКОВОДСТВО К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ ПО
МЕДИЦИНСКОЙ И БИОЛОГИЧЕСКОЙ СТАТИСТИКЕ
КРАСНОЯРСК 2003
Л.А. Шапиро, Н.Г. Шилина.
Руководство к практическим занятиям по медицинской и биологической статистике. Учебное пособие для студентов медицинских вузов. – Красноярск, 2003, 94 стр.
Рецензенты:
Горнева Е.И., доцент кафедры высшей математики Красноярского государственного технического университета, к.т.н.
Гончарова Г.Н., заведующая кафедрой СГОЗ Красноярской государственной медицинской академии д.м.н., профессор.
Новиков О.М., профессор кафедры медицинского страхования, менеджмента и маркетинга Красноярской государственной медицинской академии, д.м.н.
Рекомендуется Сибирским региональным Учебно–методическим центром высшего профессионального образования в качестве учебного пособия для студентов и аспирантов медицинских вузов.
Рекомендуется Учебно–методическим объединением по медицинскому и фармацевтическому образованию вузов России в качестве учебного пособия для студентов, обучающихся по специальности 040600–Сестринское дело.
Руководство предназначено для студентов и аспирантов медицинских вузов. В нем в общедоступной форме изложены необходимые для медико-биологических исследований статистические методы: группировка материала, составление вариационных рядов, вычисление и оценка выборочных показателей, корреляционный, регрессионный и дисперсионный анализ.
ПРЕДИСЛОВИЕ.
В настоящее время стремление к математическому выражению соответствующих закономерностей распространилось на все области знаний, в том числе на биологию и медицину. Важнейшим обстоятельством, определившим применение математико-статистических методов, явилось установление того, что многим медико-биологическим явлениям свойственны статистические закономерности, обнаруживаемые при изучении совокупностей. Так, многие экологические, генетические, цитологические, микробиологические, фармакологические и другие явления – массовые по своей природе.
|
|
|
В данном руководстве изложены элементарные основы медицинской и биологической статистики в объеме, предусмотренном программой. Оно состоит из четырех основных тем: изучение нормального закона распределения случайной величины, закономерностей малых выборок, а также корреляционного, регрессионного и дисперсионного анализа. Большое внимание уделено понятию достоверности при анализе медико-биологических данных. Изложенный материал иллюстрируется конкретными примерами из различных областей биологии и медицины. К каждой теме составлены контрольные вопросы и задания для самостоятельной работы. В Приложении собраны необходимые таблицы.
Руководство является специализированным, приспособленным для подготовки врача.
Тема 1. Изучение нормального закона распределения.
Современный количественный медико–биологический эксперимент является самостоятельным математическим исследованием, которое начинается с планирования эксперимента, т.е. организации его постановки и завершается статистической обработкой полученных результатов.
Биометрия – область научного знания, охватывающая планирование и анализ результатов количественных биологических экспериментов и наблюдений методами математической статистики. Биометрические методы представляют собой одну из важных областей применения теории вероятностей. Рассмотрим самые общие теоретические положения.
|
|
|
Множество числовых исходов медико–биологического эксперимента является случайными величинами. Случайная величина – это такая величина, которая в результате опыта может принять то или иное значение, причем неизвестно заранее какое именно. Например, рост и вес человека, число вызовов врача на дом, содержание гемоглобина в крови, уровень активности ферментов и т.д. Различают дискретные (прерывные) и непрерывные случайные величины. Дискретные случайные величины могут принимать некоторые определенные значения (счетное множество значений), например, число заболеваний, число вызовов врача, количество пораженных кариесом зубов. К непрерывным относятся такие величины, которые могут принимать на определенном интервале любые значения. К ним относятся температура тела, давление крови, вес тела, рост и т.д. Числовые значения, принимаемые случайной величиной, называются вариантами.
Пусть дискретная случайная величина принимает значения: x1, x2, x3, …. xn. Вероятности этих значений: Р1, Р2, Р3, … Рn в большинстве случаев не одинаковы, но так как все n возможных значений дискретной случайной величины представляет полную систему, то сумма их вероятностей должна быть равна 1.
Это соотношение носит название условия нормировки:
 (1)
(1)
Если известно, какой вероятностью обладает каждое значение, то тем самым задан закон распределения вероятностей. Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Закон распределения или просто распределение вероятности случайной величины является полной характеристикой, определяющей возможные значения этой величины и позволяющей сравнивать вероятности различных возможных значений. Закон распределения случайной величины может задаваться в виде таблицы, графика и формулы (аналитически).
При табличном задании закона распределения дискретной случайной величины необходимо указать ее значения и соответствующие им вероятности. Например, распределение числа вызовов врача на диспетчерском пункте скорой помощи за 15 минут может иметь вид:
Таблица 1
| x | |||||
| Р | 0,15 | 0,2 | 0,4 | 0,2 | 0,05 |
0<P<1, 

|
|
|
При графическом способе задания на оси абсцисс откладывают значения, принимаемые этой величиной, а на оси ординат – соответствующие им вероятности (рис.1). Для непрерывной случайной величины такого графика построить нельзя, так как случайная величина имеет бесчисленное множество значений, сплошь заполняющей некоторый промежуток (рис.2).
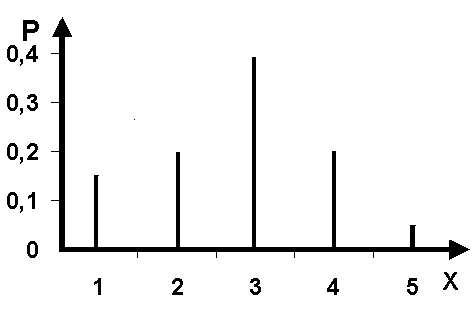
 Рис.1.Дискретное распределение. Рис.2.Непрерывное распределение.
Рис.1.Дискретное распределение. Рис.2.Непрерывное распределение.
Кроме закона распределения, дискретные и непрерывные случайные величины характеризуются числовыми характеристиками.
|
|
|


