Задания для самостоятельной работы.

 

1. Рассчитать величину коэффициента корреляции для двух выборок (y) и (x).

2. По величине полученного коэффициента корреляции записать вывод о силе и направлении связи.

3. Определить достоверность полученного коэффициента корреляции.

4. Построить эмпирическую линию регрессии.

5. Составить уравнение регрессии у по х.

6. По полученному уравнению построить график зависимости у=f(х).

7. Найти значение у для заданного х по графику и по уравнению.

8. Доказать достоверность полученной линии регрессии.

Вариант 1.

Атеросклероз

Площадь поражения артерий таза (%)	22,3	3,1	48,3	17,0	7,5	40,2	23,1	16,0	32,5	29,0
Возраст (год)

х=57

Вариант 2.

Норма

Содержание андростеронов в моче (мг/сутки)	0,82	0,90	0,98	1,06	1,20	1,29	1,48	1,42	1,40	1,08
Возраст (год)

х=50

Вариант 3.

Беременность

Концентрация пролактина в крови (нг/мл)
Срок беременности

х=6

Вариант 4.

Норма

Поверхность тела (м2)	1,1	1,5	1,2	1,3	1,9	1,3	2,0	1,7	1,5	1,7
Вес (кг)

х=35

 

Вариант 5.

Норма

Объем циркулирующей крови (л)	4,83	5,08	3,81	5,34	4,06	5,34	4,32	5,59	4,57	5,8
Рост (см)

х=176

Вариант 6.

Норма

Латентный период (мс)	15,7	20,6	25,6	34,6	48,5	66,6	96,1	127,2	73,5	178,4
Амплитуда потенциалов мозга (мкв)	2,3	4,0	7,4	4,5	6,7	10,0	9,2	10,8	8,3	15,2

х=9

 

 

Тема 4. Основы дисперсионного анализа.

 

Изменение (вариация) случайных величин вызывается одновременным действием целого ряда причин (факторов). Например, различные параметры организма (температура, артериальное давление) изменяются в зависимости от времени суток, при назначении какого–либо фармакологического препарата в различных дозах и т.д. Влияние тех или иных факторов на изучаемый признак невозможно выделить в чистом виде. Несмотря на то, что при проведении опытов стараются сохранить условия максимально однородными, все же различные опыты дают несколько неодинаковые результаты. Объясняется это тем, что на них влияют многочисленные случайные обстоятельства, многие другие неконтролируемые факторы. Поэтому возникает важная задача разложения общей изменчивости признака на составные части, с одной стороны определяемыми конкретными факторами, а с другой – вызываемыми случайными, неконтролируемыми причинами.

Раздел статистики, изучающий влияние факторов на изменчивость случайной величины, называется дисперсионным анализом. Задача дисперсионного анализа – выделить те факторы и их сочетания, которые оказывают влияние на изменение случайной величины. В зависимости от количества учитываемых факторов различают однофакторный и многофакторный дисперсионный анализ.

Для того чтобы выводы при дисперсионном анализе были обоснованы, необходимо выполнение следующих условий:

­ изучаемые факторы должны быть независимыми,

­ распределение выборочных данных должно соответствовать нормальному распределению или сводится к нему путем соответствующих преобразований.

Предположим, что мы анализируем отклонение какого–либо признака, например, (артериального давления) больного гипертонической болезнью от среднего артериального давления всех гипертоников. При этом считаем, что это отклонение вызвано действием на этот признак какого–либо определенного фактора, (например прием лекарственного препарата адельфана и т. д.)

Тогда в общем виде можно записать:

х – m =А+е, (1)

где m – средняя арифметическая генеральной совокупности (всех больных), х – конкретное значение переменной (данного больного), А – доля отклонения переменной, связанная с влиянием данного конкретного фактора (лекарственного препарата), е – остаточная часть отклонения, не объяснимая влиянием данного фактора. Это результат случайных отклонений, вызванный всеми неконтролируемыми и неопределенными факторами.

При достаточном влиянии изучаемого фактора значение А будет в достаточной степени превышать значение е. По степени превышения А над е можно судить о том, насколько достоверно влияние данного фактора.

Более сложный случай – отклонение переменной х от средней арифметической генеральной совокупности m под влиянием двух причин: влияния факторов А и В. Например, фактором А может быть возраст, а фактором В – пол (мужчина или женщина).

(1a)

Здесь А – доля отклонения, связанная с влиянием фактора А; В – доля отклонения, связанная с влиянием фактора В; АВ – доля отклонения, связанная с влиянием не отдельных факторов А и В, а их взаимодействия; е – остаточная, случайная часть отклонения. Очевидно, что схему можно усложнять и дальше.

Степень изменения всех признаков и отклонение их от средней арифметической ряда характеризуется дисперсией D(х):

D(х)= (2)

Общая дисперсия будет складываться из двух частей: дисперсии, обусловленной действием фактора А и дисперсии, определяемой другими неконтролируемыми (случайными) причинами.

D_общ=D_факт +D_случ (3)

Воздействие фактора оценивается критерием Фишера: отношением факторной дисперсии (D_факт) к случайной дисперсии D_случ:

F= (4)

Если факторная дисперсия окажется меньше случайной, то нет необходимости прибегать к критерию Фишера. Ясно, что влияние фактора не ведет к заметной вариации результатов. В этом случае влиянием фактора можно пренебречь. При F > 1 полученные значения критерия Фишера сравниваются с критическими значениями F_кр. по таблице 5 Приложения. В медико–биологических исследованиях принято, если F>F_кр, соответствующему вероятности Р=0,95( =0,05), то влияние фактора существенно. Если вероятность Р<0,95, фактор не влияет на изучаемый признак.

Обычно каждый изучаемый в эксперименте фактор А имеет не одно, а несколько значений, которые называют градациями или уровнями фактора А (А₁,А₂,. …). Уровни фактора могут быть как дискретными, так и непрерывными случайными величинами. В первом случае они принимают точечные значения, во втором – интервальные.

Рассмотрим однофакторный дисперсионный анализ для малых групп на примере анализа длительности терапевтического действия лекарственного препарата (в часах) в зависимости от дозировки (0,25; 0,5; 0,75 и 1мг). Обследовано 4 группы по 10 человек. Результаты занесены в таблицу 1.

 

Результаты определения длительности терапевтического действия

лекарственного препарата (в часах).

Таблица 1

Обследованные	Дозы препарата
0,25	0,5	0,75

= 48,4 48,0 76,4 95,4

В нашем примере фактором А является доза лекарственного препарата, а уровнями – концентрации в мг: А₁=0,25, А₂=0,5, А₃=0,75, А₄=1. Общее количество групп: а=4. В каждой группе проведено n=10 измерений. В итоге получаем таблицу из N= вариант изучаемого признака (имеющегося или нет) в зависимости от фактора А.

Рассчитаем средние арифметические в каждой группе: . Мы видим, что средние арифметические (48,4; 48,0; 76,4; 95,4) в группах различаются. Необходимо доказать, что эти различия связаны с действием фактора (дозы препарата).

Для рассмотрения общих формул дисперсионного анализа представим данные измерений в виде общей таблицы (таблица 2). Обычно разные уровни фактора принято обозначать индексом i (i меняется от 1 до а), а отдельные варианты в группе – индексом j (j меняется от 1 до n). Поэтому каждую варианту, независимо от того, где она находится можно обозначить x_ij.

 

Схема варьирования при различии групп по одному фактору.

Таблица 2

Номер наблюдения (j)	Уровни фактора(i)
			...	I	a
	x11	x21	x31		xi1	xa1
	x12	x22	x32		xi2	xa2
	x13	x23	x33		xi3	xa3
...
j	x1j	x2j	x3j		xij	xaj
n	x1n	x2n	x3n		xin	xan
Суммы по группам: Тi	åx1 =T1	åx2 =T2	åx3 =T3		åxi =Ti	åxa =Ta
Средние по группам:

 

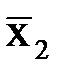
Суммы вариант по каждой группе обозначены Т_i: (Т₁,Т₂... Т_а).

Общая сумма всех вариант: T=åx_ij

Средние арифметические в каждой группе – ().

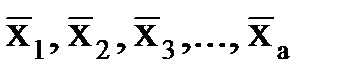Общую среднюю арифметическую величину для всех вариант обозначим – .

С учетом этих обозначений можно приступить к рассмотрению типов варьирования данных в таблице 2:

Общее варьирование всех вариант (х_ij), независимо от того, в какой группе они находятся, вокруг общей средней характеризуется дисперсией D_общ.

Так как, согласно формуле (2) дисперсия равна сумме квадратов отклонений вариант от своей средней деленной на число степеней свободы, то:

 

(5)

где N= 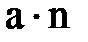– число всех вариант. df_общ.=N–1 – число степеней свободы. Значок ij около знака суммы обозначает, что суммирование производится по всем вариантам всех групп.

Варьирование групповых средних или средних каждого уровня данного изучаемого фактора вокруг общей средней , характеризуется факторной дисперсией D_факт.. Число степеней свободы df_факт. для дисперсии групповых средних:

df_факт=a – 1.

; (6)

n_i – среднее число вариант в каждой группе, n – если число вариант в группах одинаково.

Варьирование вариант х_ij внутри каждой группы вокруг каждой групповой средней характеризует случайная или остаточная дисперсия D_случ.

Для случайной вариации вариант внутри групп число степеней свободы:

df _случ.= ,

(7)

Сумма чисел степеней свободы для групповых средних и для вариации внутри групп должна равняться числу степеней свободы для общей дисперсии:

(N – a) + (a – 1) = N – 1

Теоретические формулы для однофакторного дисперсионного анализа.

Таблица 3

Источник варьирования	Сумма квадратов SS (числитель)	Число степеней свободы df (знаменатель)	Формулы для дисперсии MS
Общее (все варианты)		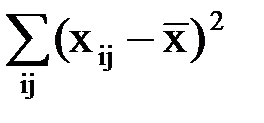N – 1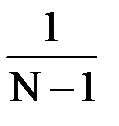
Групповые средние (фактор А)		a –1
Варианты внутри групп (случайные отклонения)		N – a

 

Вариация групповых средних имеет сложную природу, они являются выборочными и, в свою очередь, варьируют вокруг средней арифметической генеральной совокупности m с некоторой ошибкой. Поэтому, значение D_факт. не является абсолютным. Чтобы учесть этот факт, числитель формул (5)–(7) называют суммой квадратов и обозначают SS, а дисперсии – средними квадратами и обозначают MS.

Вычисление сумм квадратов отклонений (SS) в числителях формул (5)–(7) достаточно трудоемко, поэтому на практике пользуются рабочими формулами, в которых сумма квадратов отклонений вычисляется по значениям вариант, без вычисления средних арифметических значений согласно формуле (2):

(8)

С учетом принятых выше обозначений: Т_i – сумма всех вариант в группе, Т – сумма всех вариант в таблице, рабочие формулы будут выглядеть следующим образом:

· Сумма квадратов отклонений для MS_общ.:

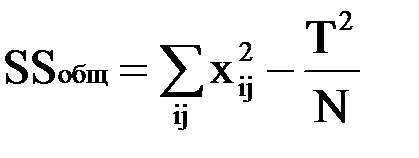(9)

· Сумма квадратов отклонений для MS_факт:

SS_фак= (10)

Нет необходимости вычислять все 3 суммы квадратов. Сумма квадратов отклонений для случайной дисперсии вычисляется вычитанием формул (9) и (10):

SS_случ=SS_общ – SS_фак

 

Сводка рабочих формул для однофакторного дисперсионного анализа.

Таблица 4

Источник варьирования	Сумма квадратов SS (числитель)	Число степеней свободы df (знаменатель)	Формулы для среднего квадрата MS
Общее (всеварианты)		N – 1
Групповые средние (фактор А)		a –1	()
Варианты внутри групп (случайные отклонения)	SSслуч=SSобщ – SSфак	N – a

Таким образом, для рассмотрения влияния уровней фактора А на исследуемую величину необходимо определить:

1. Сумму квадратов всех вариант таблицы.

2. Сумму всех вариант таблицы и квадрат этой суммы – Т².

3. Суммы вариант в каждой группе – Т_i, квадраты этих сумм – и сумму квадратов сумм по всем группам .

Результаты определения длительности воздействия лекарственного препарата сведем в таблицу 5, добавив квадраты исследуемых величин.

Таблица 5

Уровни фактора А_i

№	A1	A2	A3	A4
x1j	x2j	x3j	x4j
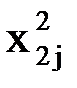
=	48,4		76,4	95,4		=201794
Ti=
=
=
T=
T2=

 

1. Сумма квадратов 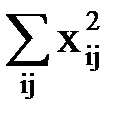всех вариант=201794.

2. Сумма всех вариант таблицы T=2682.

3. Квадрат суммы всех вариант: Т² =7193124.

4. Суммы вариант в каждой группе: Т₁=484, Т₂=480, Т₃=764, Т₄=954.

Квадраты этих сумм: =234256, =230400, =583696, =910116.

5. Общая сумма квадратов групповых сумм: =1958468.

На основании этих данных, вычислим необходимые нам компоненты:

· Сумма квадратов SS_общ. для общей вариации:

SS_общ.= =201794– =21965,9

· Сумма квадратов для вариации между группами SS_факт:

=16018,7

Средний квадрат, характеризующий факторную дисперсию MS_факт.:

MS_факт.= = =5339,567

· Сумма квадратов для вариации внутри групп SS_случ.:

SS_случ.=SS_общ.– SS_факт.=21965,9–16018,7=5947,2

Средний квадрат, характеризующий случайную дисперсию MS_случ.:

MS_случ. = =165,2

Случайная дисперсия является мерой случайной ошибки для всех проведенных измерений. Так как MS_факт > MS_случ. определим фактическое значение критерия Фишера:

F_факт.= = =32,32

По таблице 5 Приложения определим F_кр для доверительной вероятности P=0,95 (. Определение F_кр производится следующим образом: в первой строке таблицы 5 Приложения приведены степени свободы для большей дисперсии df₁. В нашем случае это df_факт.=3. В левом столбце – значения степеней свободы для меньшей дисперсии: df_случ.=36. Вся таблица составлена для одного уровня вероятности: P=0,95 (.

df1 df2				…
…
			2,84

 

На пересечении значений 3 и 40 (36 – нет) находим F_кр.=2,84. F_факт>F_кр, следовательно влияние фактора статистически достоверно.

Вывод. При анализе длительности терапевтического действия лекарственного препарата (в часах) в зависимости от дозировки (0,25; 0,5; 0,75 и 1 мг) были произведены измерения у 4 групп больных. Средние арифметические значения в каждой группе отличаются. Проведенный дисперсионный анализ доказал, что с вероятностью Р>0,95 эти различия не случайны, а связаны с влиянием фактора – дозы лекарственного препарата.

Мы рассмотрели пример, когда число опытов при каждом уровне фактора одинаков и равен n. Если число наблюдений в группах неодинаково, то в формуле (10) для суммы квадратов факторной дисперсии (SS_факт) квадраты сумм вариант в каждой группе нужно поделить на число наблюдений в этой группе (n_i)

, (11)

Например, в первой группе число наблюдений n₁=5, во второй: n₂=4:

.

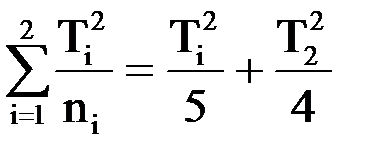При наличии влияния фактора часто возникает необходимость оценить меру (или силу) его влияния и долю в сумме влияния всех факторов. Мы уже отмечали выше, что величина MS_факт. не является абсолютным значением факторной дисперсии, так как она имеет сложную структуру, обусловленную наличием случайных ошибок (D_случ.) в каждой группе по сравнению с генеральной совокупностью. Так как MS_случ.=D_случ., при однофакторном дисперсионном анализе абсолютное значение факторной дисперсии можно оценить как:

D_факт.= (12)

Сила влияния фактора 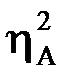определяется по формуле:

= (13)

В нашем примере: D_факт.= =517,437,

= или 76% от действия всех факторов приходится на дозу препарата, 24% – приходится на долю случайных факторов. Результаты дисперсионного анализа можно представить в итоговой таблице:

 

 

Результаты однофакторного дисперсионного анализа данных.

Таблица 6

Источник варьирования	Сумма квадратов SS	Число степеней свободы df	Средний квадрат MS (дисперсия)	F факт.	F табл. при Р=0,95	Сила влияния фактора
Общее	21965,9
Фактор А (доза препарата)	16018,7		5339,567	32,32	2,84	0,76
Случайные отклонения	5947,2		165,2			0,24

Если действие фактора доказано, можно продолжить статистическую обработку результатов анализом средних арифметических величин по группам. Этот анализ позволяет выявить направленность действия фактора, а также область максимальной чувствительности к действию фактора. Например, если уровнями фактора являются дозы какого – либо лекарственного препарата, то можно выявить наиболее эффективную дозу.

Рис.1.Зависимость терапевтического воздействия (часы)

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: