 |
Тема 4. Дифференциал функции
|
|
|
|
Тема 1. Функции
В теме 1 рассматриваются следующие вопросы
1.1. Понятие множества. Действительные числа и числовые множества.
1.2. Понятие функции. Свойства функций. Способы задания функций.
1.3. Явная, неявная, сложная и обратная функции
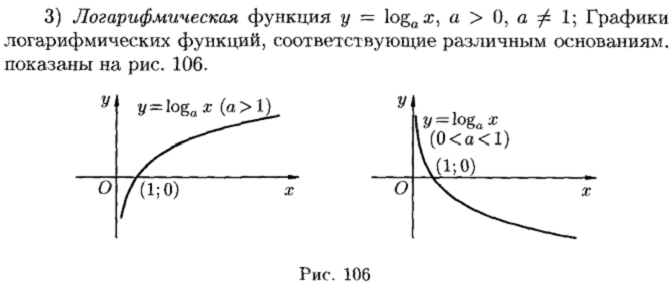
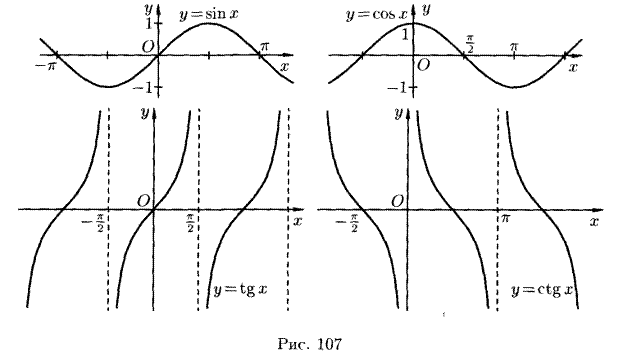
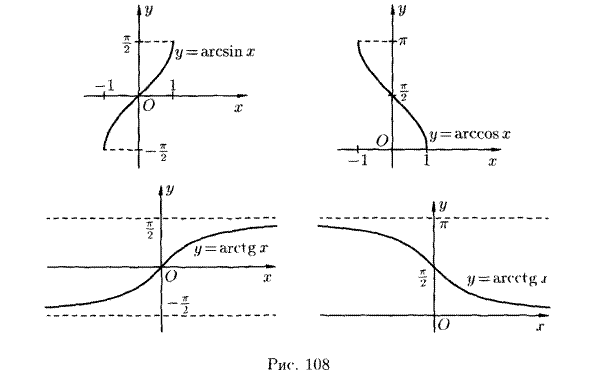
1.4. Понятие элементарной функции. Графики основных элементарных функций.
Понятие множества. Действительные числа
И числовые множества
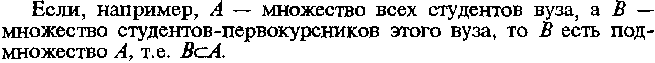
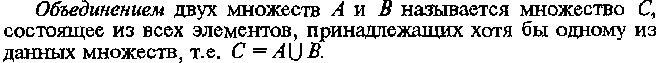
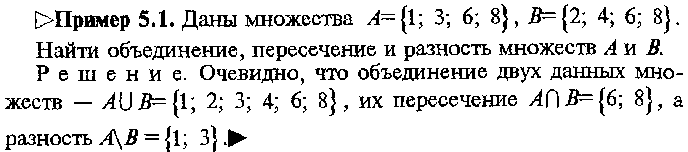
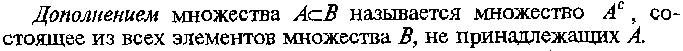
Понятие функции. Свойства функций.
Способы задания функций
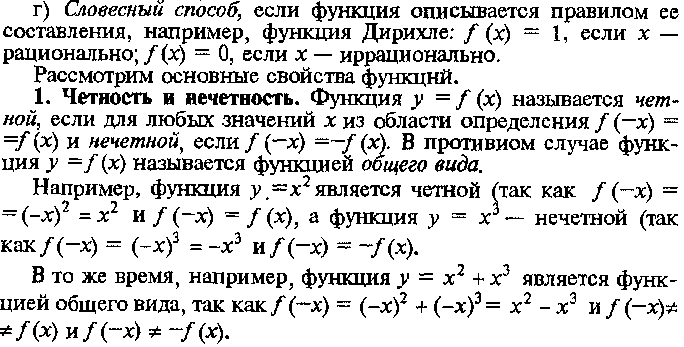
Явная, неявная, сложная и обратная функции
Понятие элементарной функции.
Графики основных элементарных функций
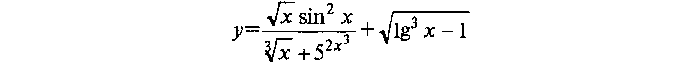
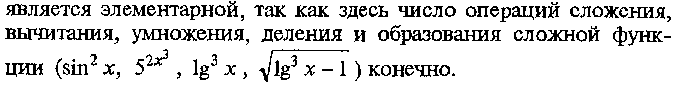
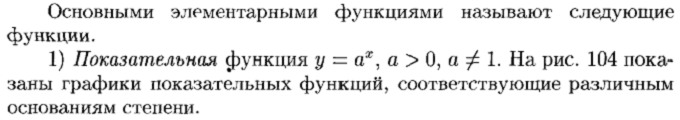
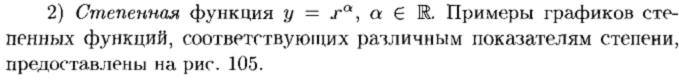
Тема 2. Пределы и непрерывность
В теме 2 рассматриваются следующие вопросы:
2.1. Числовая последовательность.
2.2. Предел числовой последовательности.
2.3. Предел функции в точке и в бесконечности.
2.4. Односторонние пределы.
2.5. Бесконечно малые функции (величины).
2.6. Сравнение бесконечно малых величин. Эквивалентные бесконечно малые.
2.7. Бесконечно большие функции (величины).
2.8. Основные теоремы о пределах.
2.9. Признаки существования предела.
2.10. Первый и второй замечательные пределы.
2.11. Непрерывность функции в точке и на промежутке.
2.12. Свойства функций, непрерывных в точке и на промежутке.
2.13. Техника вычисления пределов.
Числовая последовательность
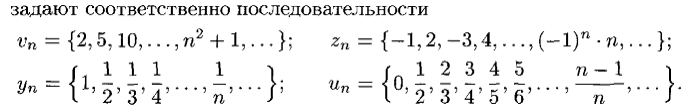
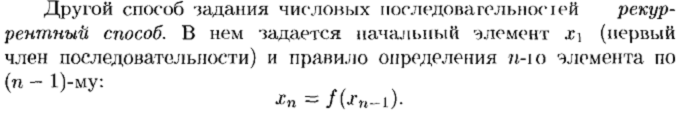
Предел числовой последовательности
Рассмотрим числовую последовательность 
.
приближаются к числу 1 по мере увеличения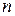 
. При этом абсолютная величина разности 
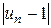становится все меньше и меньше. Действительно, 
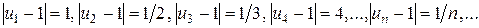, то есть с ростом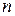 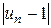будет меньше любого, сколь угодно малого положительного числа.
|
|
|
Предел функции в точке и в бесконечности
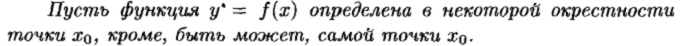
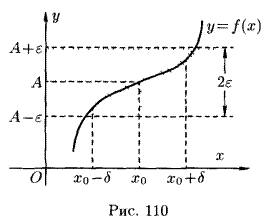
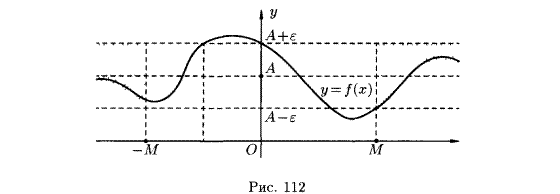
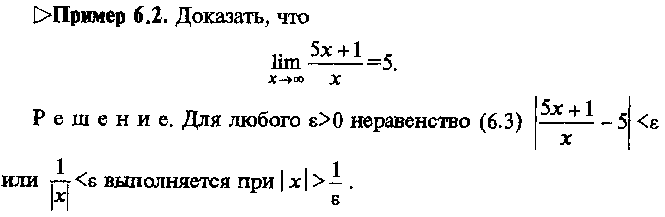
Односторонние пределы
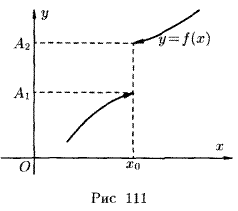
Бесконечно малые функции (величины)
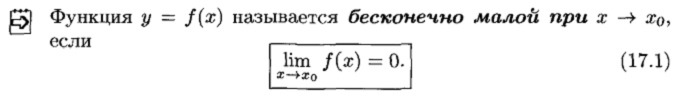
Отметим свойства бесконечно малых величин.
В качестве примера приведем доказательство теоремы 17.1.
Рассмотрим связь бесконечно малых величин с пределами функций.
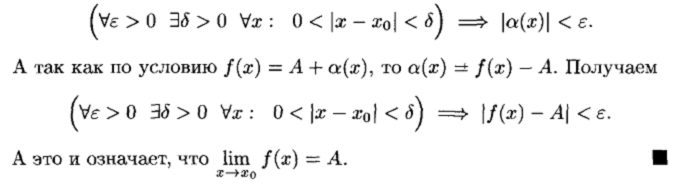
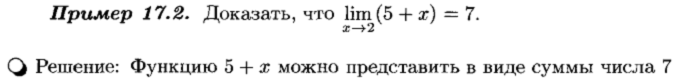
Сравнение бесконечно малых величин.
Эквивалентные бесконечно малые
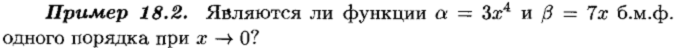
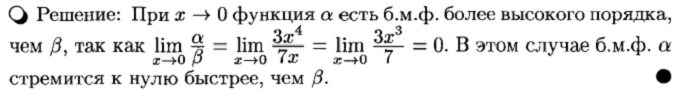
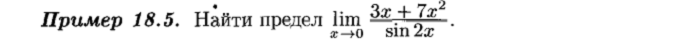
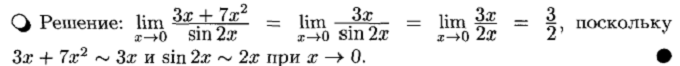
Бесконечно большие функции (величины)
Отметим свойства бесконечно больших величин.
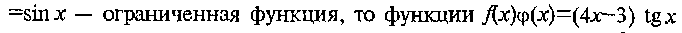
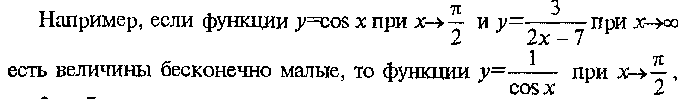
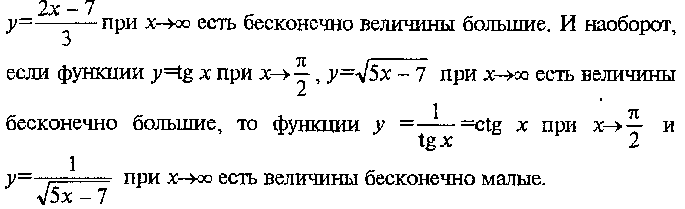
Основные теоремы о пределах
В качестве примера приведем доказательство теоремы 17.7.
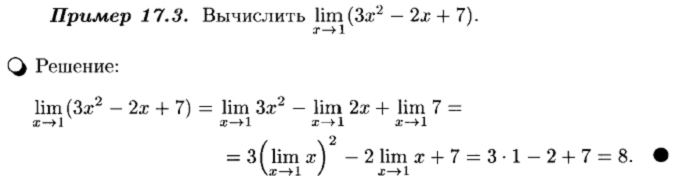
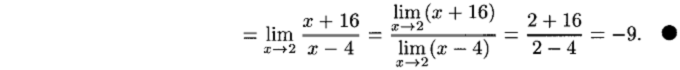
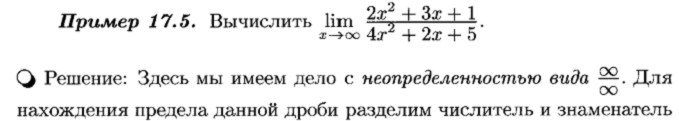
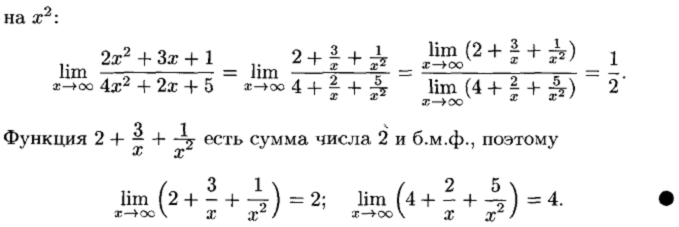
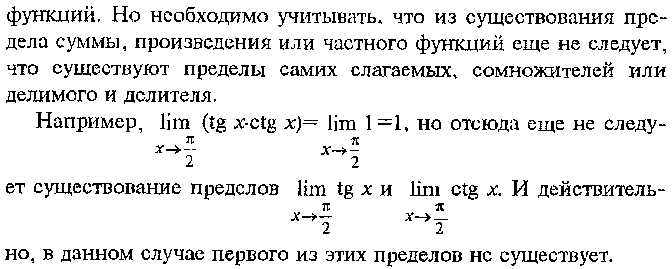
Признаки существования предела
Первый и второй замечательные пределы
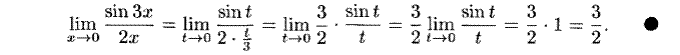
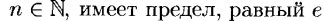
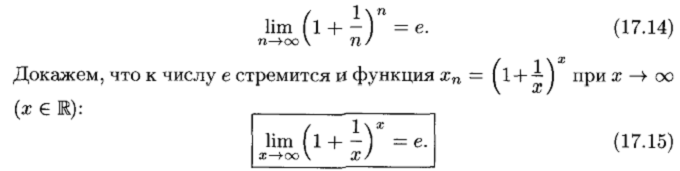
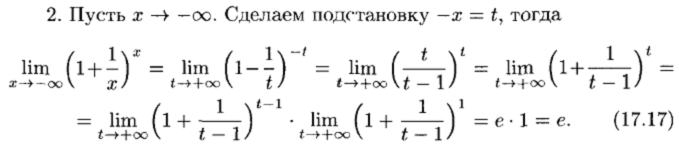
Непрерывность функции в точке и на промежутке
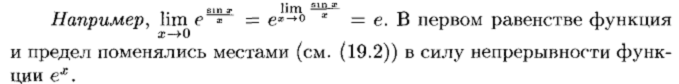
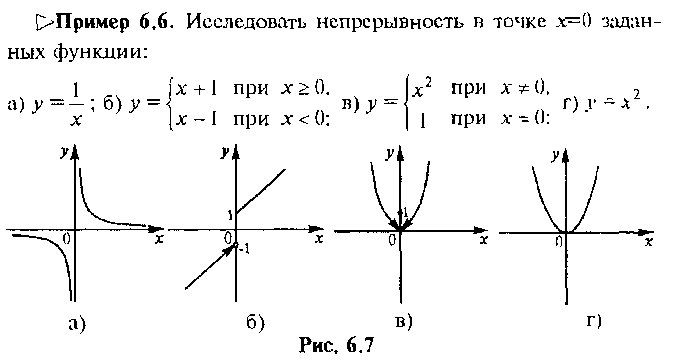
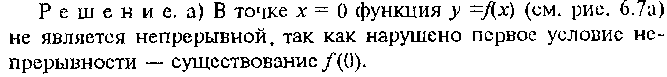
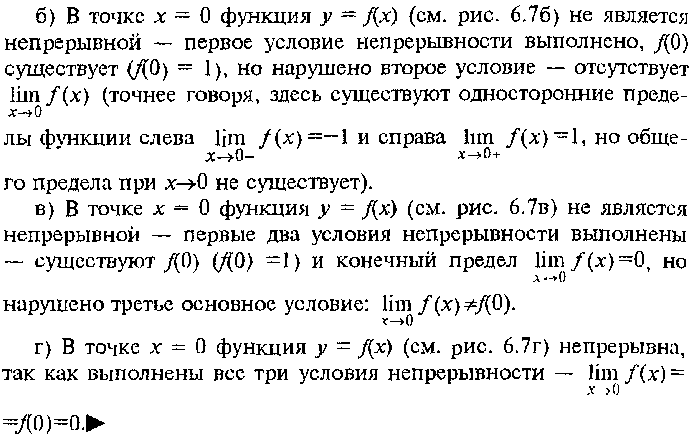
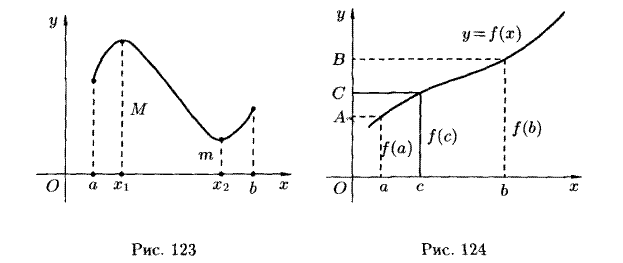
Свойства функций, непрерывных в точке
И на промежутке
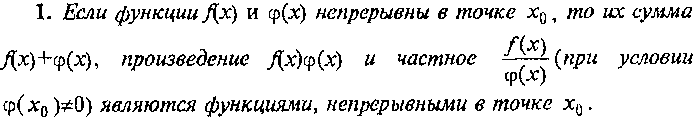
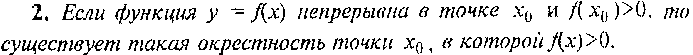
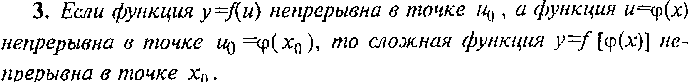
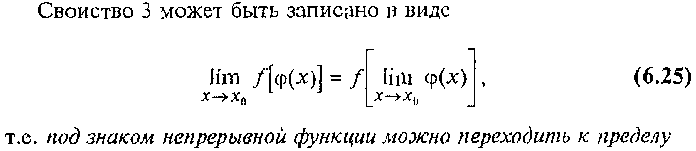
Техника вычисления пределов
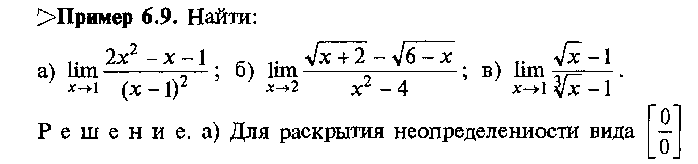
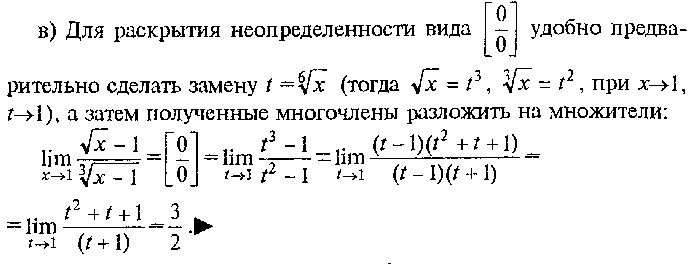
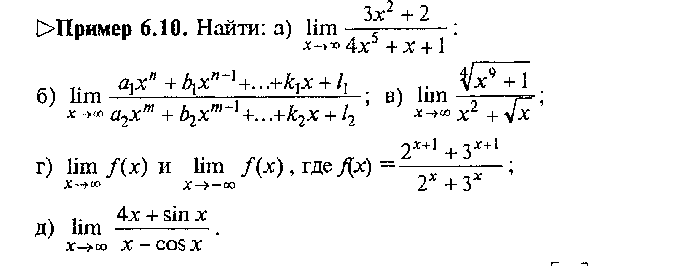
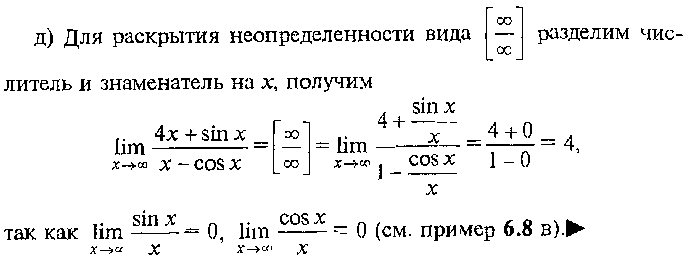
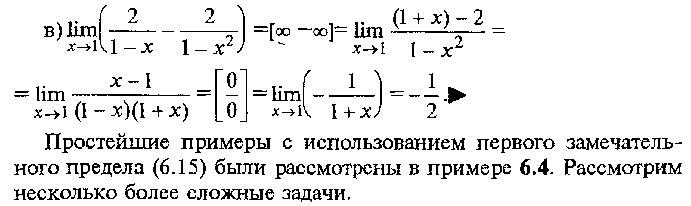
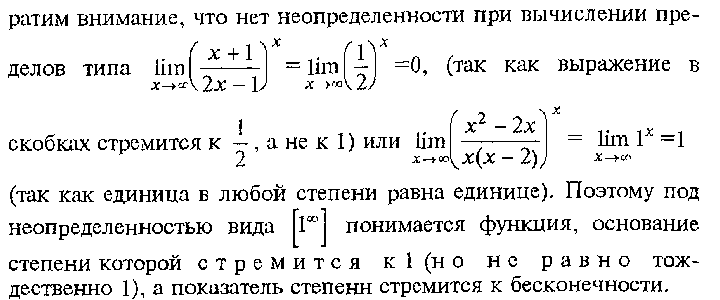
Тема 3. Производная
В теме 3 рассматриваются следующие вопросы:
3.1. Задачи, приводящие к понятию производной.
3.2. Определение производной. Механический и геометрический смысл производной.
3.3. Связь между непрерывностью и дифференцируемостью функции.
3.4. Основные правила дифференцирования.
3.5. Таблица производных.
3.6. Производная сложной и обратной функции.
3.7. Производная неявной функции.
3.8. Логарифмическое дифференцирование.
3.9. Производные высших порядков.
3.10. Техника вычисления производной.
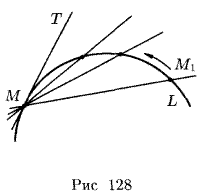
Задачи, приводящие к понятию производной
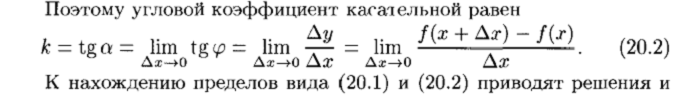
Определение производной. Механический
|
|
|
И геометрический смысл производной
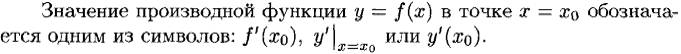
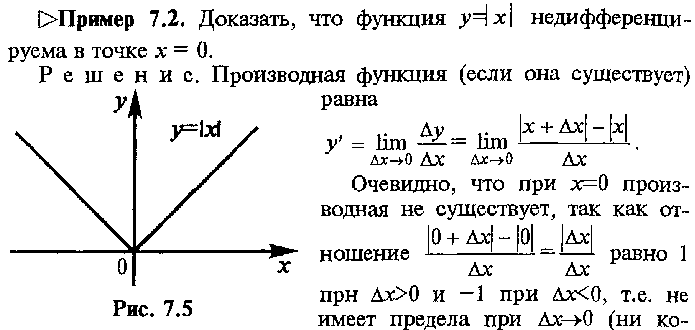
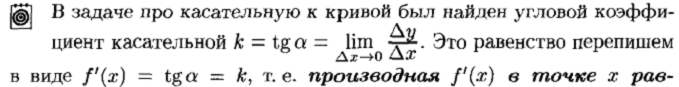
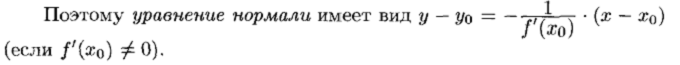
Связь между непрерывностью
И дифференцируемостью функции
Основные правила дифференцирования
В качестве примера докажем теорему 20.2.
Таблица производных
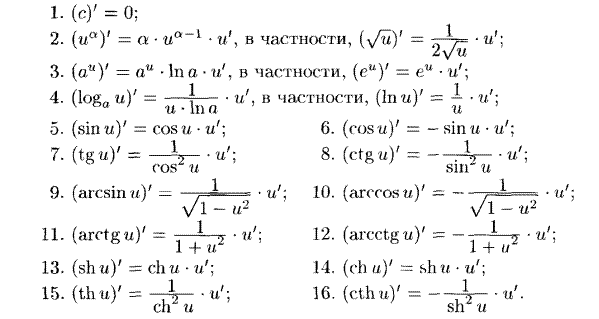
Производная сложной и обратной функции
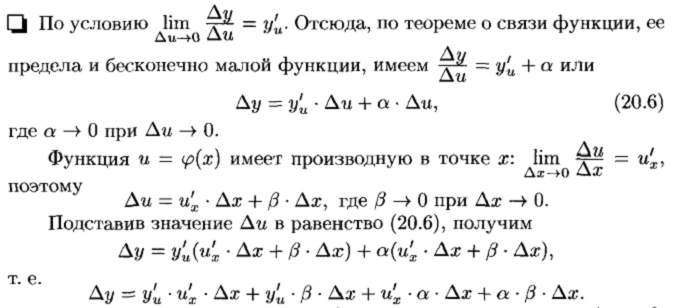
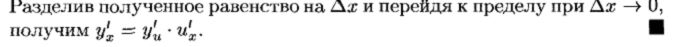
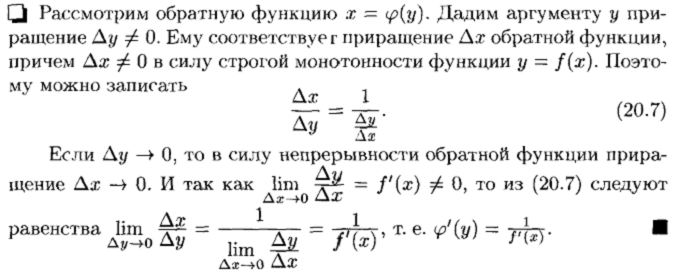
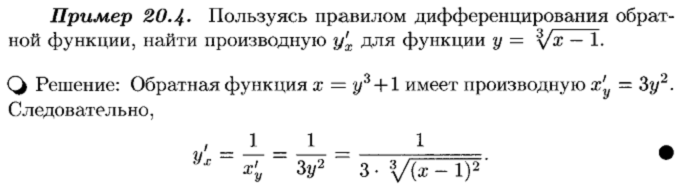
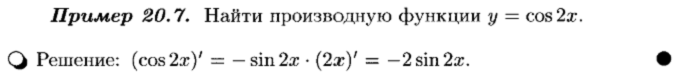
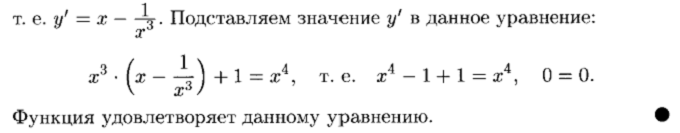
Производная неявной функции
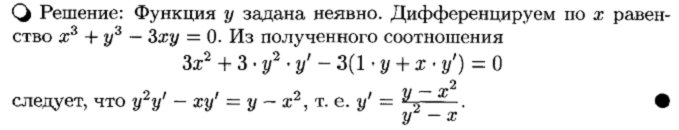
Логарифмическое дифференцирование
Производные высших порядков
Техника вычисления производных
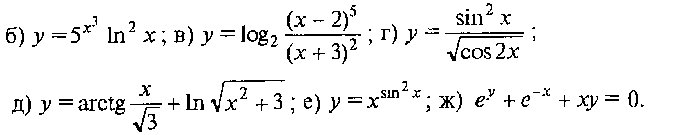
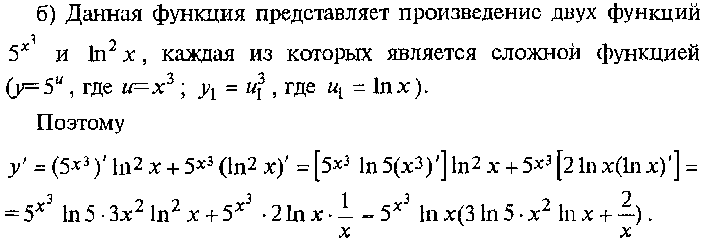
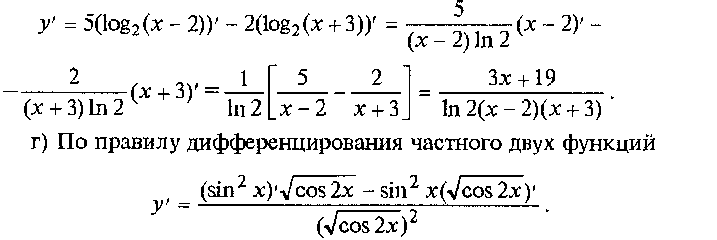
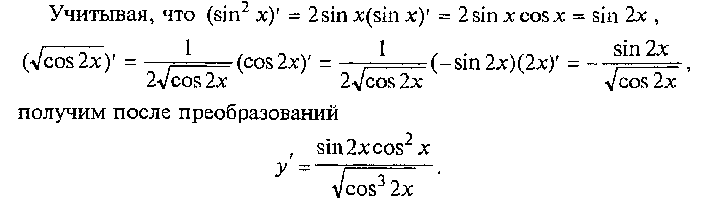
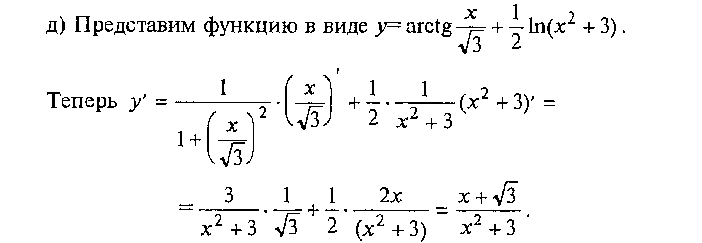
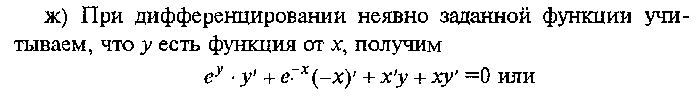
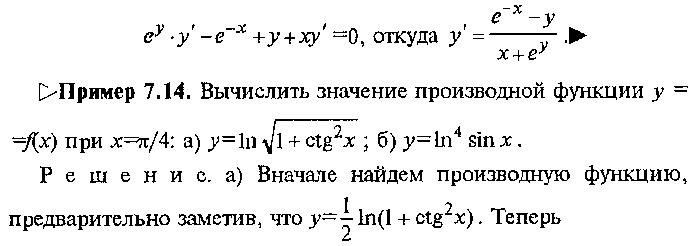
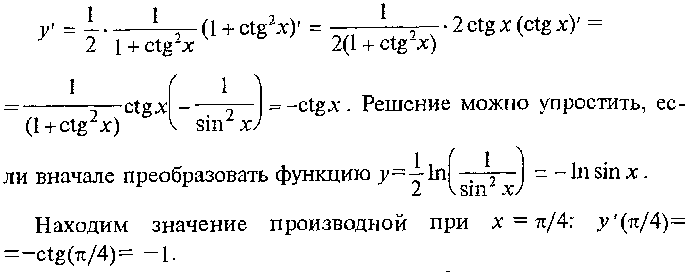
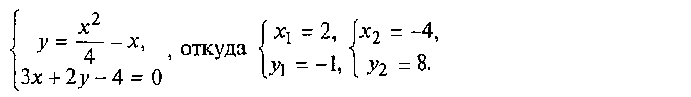
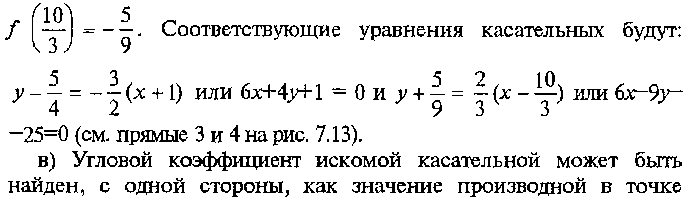
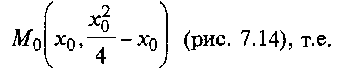
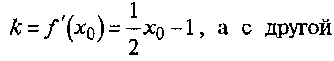
стороны, как угловой коэффициент прямой, проходящей через точку
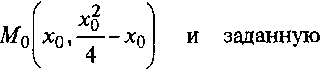
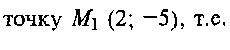
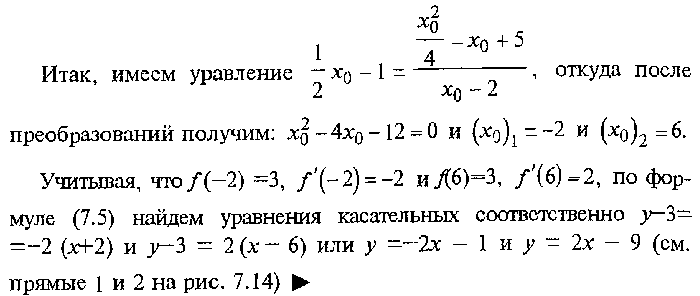
Тема 4. Дифференциал функции
В теме 4 рассматриваются следующие вопросы:
4.1. Понятие дифференциала функции.
4.2. Геометрический смысл дифференциала.
4.3. Свойства дифференциала и его инвариантность.
4.4. Применение дифференциала к приближенным вычислениям.
4.5. Дифференциалы высших порядков.
|
|
|
