 |
Вычисление объёма тела вращения
|
|
|
|
Приближенное вычисление определенного интеграла
По формуле трапеций
Тема 9. Дифференциальные уравнения
В теме 9 рассматриваются следующие вопросы:
9.1. Общие сведения о дифференциальных уравнениях.
9.2. Дифференциальные уравнения первого порядка: теорема существования и единственности решения, задача Коши.
9.3. Неполные дифференциальные уравнения первого порядка.
9.4. Дифференциальные уравнения с разделяющимися переменными.
9.5. Однородные дифференциальные уравнения первого порядка.
9.6. Линейные дифференциальные уравнения первого порядка.
Общие сведения о дифференциальных уравнениях
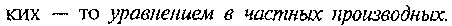
Например, 
- дифференциальное уравнение третьего порядка.
Например, 
9.2. Дифференциальные уравнения первого порядка:
Теорема существования и единственности решения,
Задача Коши
Пусть дано дифференциальное уравнение первого порядка
Задача отыскания частного решения дифференциального уравнения (12.7), удовлетворяющего начальному условию 
называется задачей Коши. Приведенная теорема устанавливает условие существования и единственности решения задачи Коши.
Неполные дифференциальные уравнения
Первого порядка
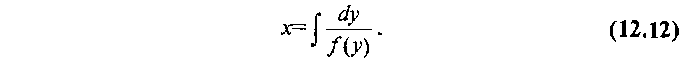
Дифференциальные уравнения
С разделяющимися переменными
или 
Замечание.
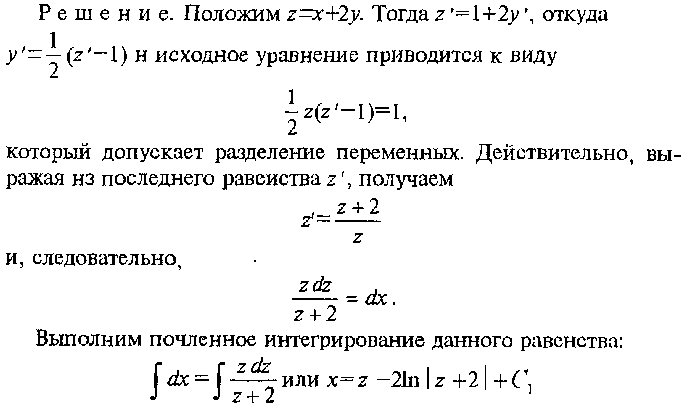
Однородные дифференциальные уравнения
Первого порядка
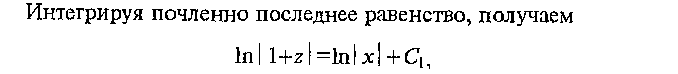
Линейные дифференциальные уравнения
Первого порядка
Замечание. Рассмотренный метод, известный также как метод Бернулли, применим и для решения уравнения вида
|
|
|
называемого уравнением Бернулли.
Тема 10. Числовые ряды
В теме 10 рассматриваются следующие вопросы:
10.1. Общие сведения о числовых рядах. Свойства сходящихся рядов.
10.2. Необходимый признак сходимости числового ряда. Гармонический ряд.
10.3. Достаточные признаки сходимости знакоположительных рядов.
10.4. Признаки Даламбера и Коши.
10.5. Интегральный признак Коши.
10.6. Знакочередующиеся ряды. Признак Лейбница.
10.7. Знакопеременные ряды.
10.8. Абсолютная и условная сходимость.
10.9. Сходимость степенных рядов.
10.10. Свойства степенных рядов.
10.11. Ряд Тейлора и Маклорена. Разложимость в ряд Маклорена бесконечно дифференцируемой функции.
10.12. Разложение в ряд Маклорена некоторых элементарных функций.
10.13. Применение степенных рядов к приближенным вычислениям.
Общие сведения о числовых рядах.
Свойства сходящихся рядов
Необходимый признак сходимости числового ряда. Гармонический ряд
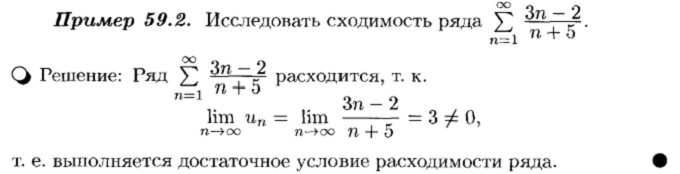
Достаточные признаки сходимости знакоположительных рядов
Признаки Даламбера и Коши
Интегральный признак Коши
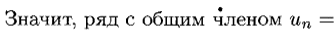
Знакочередующиеся ряды. Признак Лейбница
Знакопеременные ряды
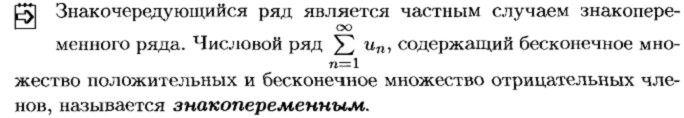
Абсолютная и условная сходимость
Сходимость степенных рядов
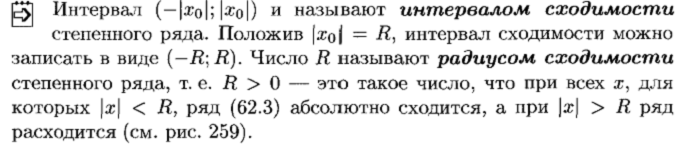
Свойства степенных рядов
Ряд Тейлора и Маклорена. Разложимость в ряд Маклорена бесконечно дифференцируемой функции
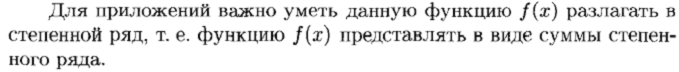
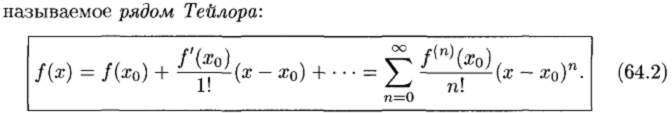
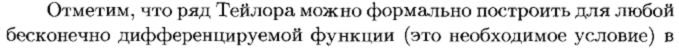
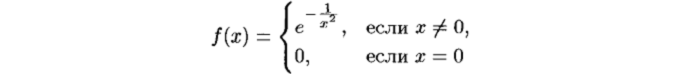
Разложение в ряд Маклорена
Некоторых элементарных функций
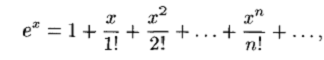
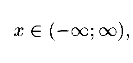
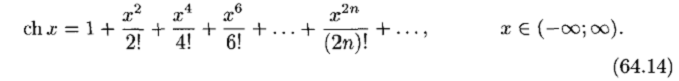
Таким образом, справедлива формула (64.4).
Применение степенных рядов к приближенным вычислениям
|
|
|
|
|
|
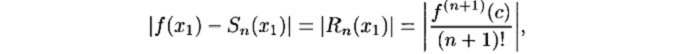
