 |
Понятие дифференциала функции
|
|
|
|
Геометрический смысл дифференциала
4.3. Свойства дифференциала и его инвариантность
Применение дифференциала к приближенным вычислениям
Дифференциалы высших порядков
Тема 5. Приложения производной
В теме 5 рассматриваются следующие вопросы:
5.1. Теоремы Роля, Лагранжа и Коши.
5.2. Правило Лопиталя.
5.3. Экстремум функции. Необходимые и достаточные условия экстремума функции.
5.4. Наибольшее и наименьшее значения функции на отрезке.
5.5. Выпуклость графика функции. Точки перегиба.
5.6. Асимптоты графика функции.
5.7. Общая схема исследования функции и построения её графика.
5.8. Формула Тейлора (Маклорена)
Теоремы Роля, Лагранжа и Коши
Теорема Лагранжа имеет простой геометрический смысл. Запишем формулу (25.2) в виде
есть угловой коэффициент секущей АВ, а величина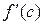 
– угловой коэффициент касательной к кривой в точке с абсциссой x=c.
Правило Лопиталя
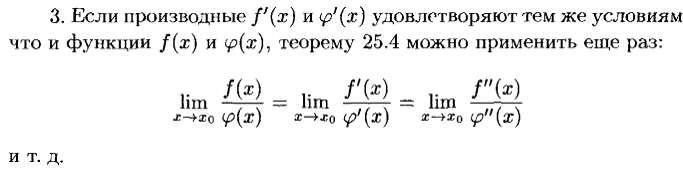
Экстремум функции. Необходимые и достаточные условия экстремума функции
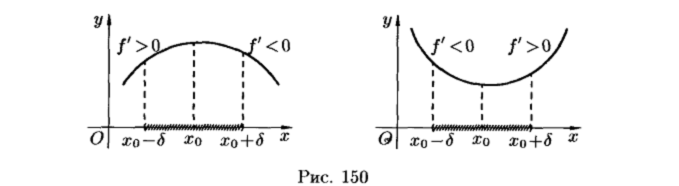
Наибольшее и наименьшее значения функции на отрезке
Выпуклость графика функции. Точки перегиба
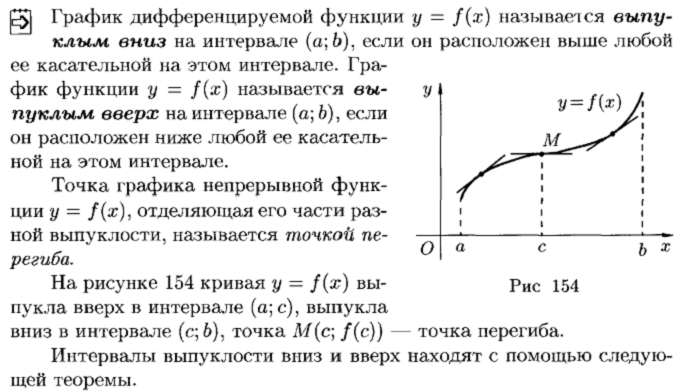
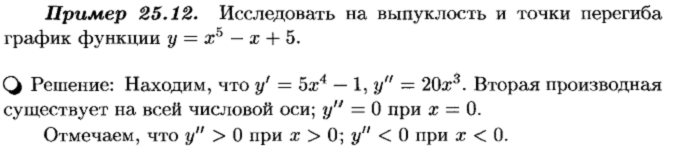
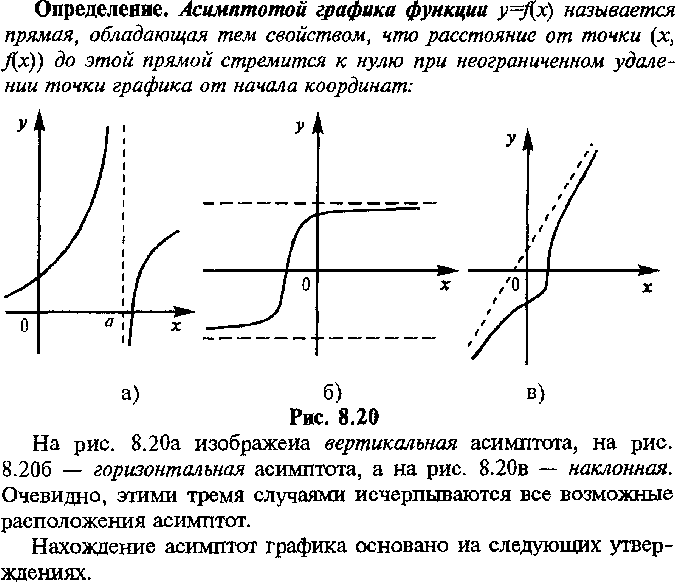
Асимптоты графика функции
Общая схема исследования функции
И построения графика
Формула Тейлора (Маклорена)
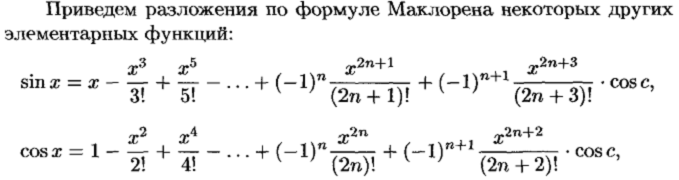
Тема 6. Функции нескольких переменных
В теме 6 рассматриваются следующие вопросы:
6.1. Функции двух переменных. Основные понятия.
|
|
|
6.2. Линии уровня функции двух переменных.
6.3. Предел функции двух переменных.
6.4. Непрерывность функции двух переменных.
6.5. Свойства функций, непрерывных в ограниченной замкнутой области.
6.6. Частные производные функции двух переменных.
6.7. Дифференцируемость и полный дифференциал функции двух переменных.
6.8. Частные производные высших порядков.
6.9. Дифференциалы высших порядков.
6.10. Производная сложной функции.
6.11. Производная функции по направлению. Градиент.
6.12. Экстремум функции двух переменных. Необходимое и достаточное условия экстремума.
6.13. Условный экстремум функции двух переменных.
Метод множителей Лагранжа.
6.14. Наибольшее и наименьшее значения функции в замкнутой области.
6.15. Эмпирические формулы и метод наименьших квадратов. Система нормальных уравнений.
Функции двух переменных. Основные понятия
костям 
и 
представляют параболы (например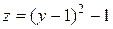, при 
, при 
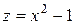и т. д.). В сечении поверхности координатной плоскостью 
, т.е. плоскостью 
, получается окружность 
. График функции представляет поверхность, называемую параболоидом (см. рис. 15.2).
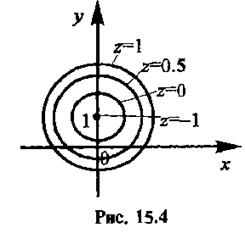
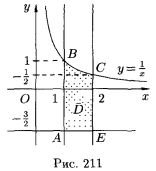
Линии уровня функции двух переменных
температуры.
Пример. Построить линии уровня функции 
.
Предел функции двух переменных
Непрерывность функции двух переменных
Свойства функций, непрерывных в ограниченной замкнутой области
Частные производные функции двух переменных
Дифференцируемость и полный дифференциал
Функции двух переменных
Частные производные высших порядков
Дифференциалы высших порядков
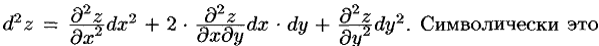
Производная сложной функции
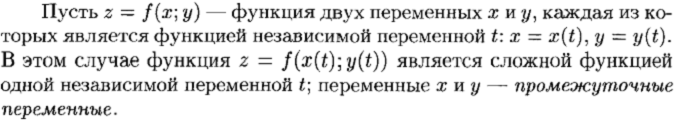
Производная функции по направлению. Градиент
|
|
|
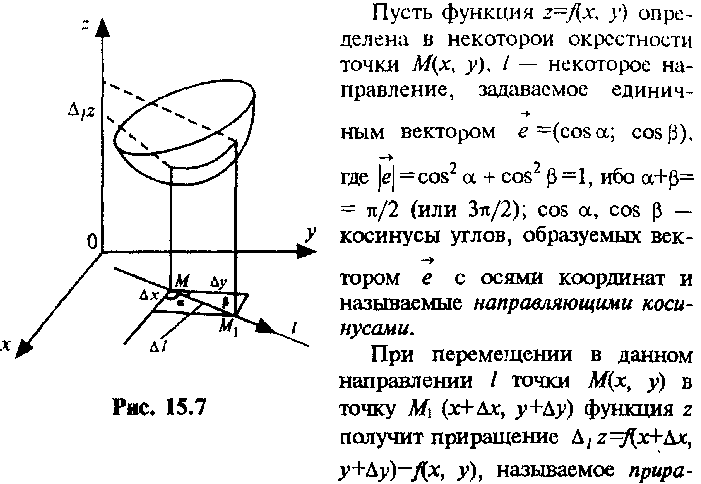
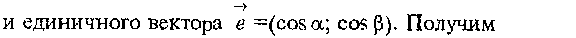
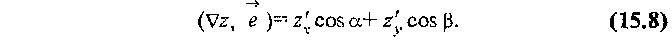
Экстремум функции двух переменных.
Необходимое и достаточное условия экстремума
Условный экстремум функции двух переменных.
Метод множителей Лагранжа
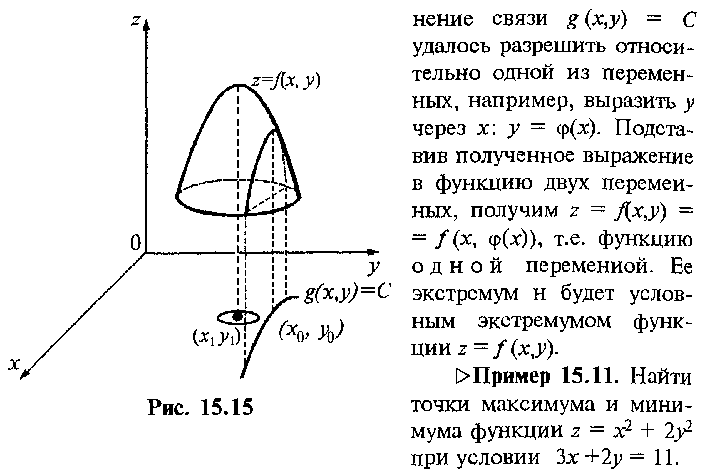
Пример. Найти точки экстремума функции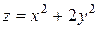 
при условии 
, используя метод множителей Лагранжа.
Решение. Составляем функцию Лагранжа 
. Приравнивая к нулю её частные производные, получим систему уравнений
Наибольшее и наименьшее значения функции
В замкнутой области
Найдем все критические точки:
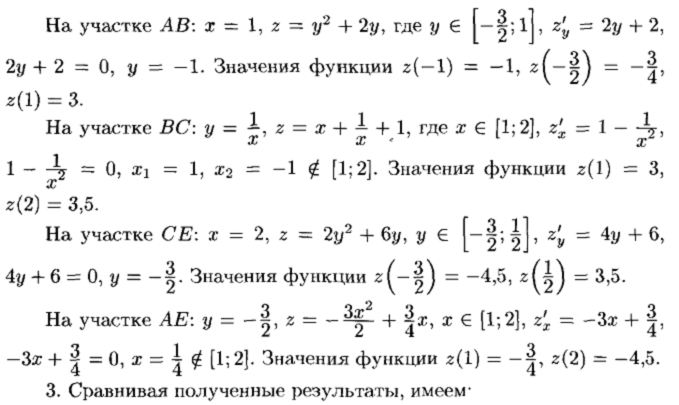
Эмпирические формулы и метод наименьших квадратов. Система нормальных уравнений
была минимальной.
|
|
|
