Производная есть отношение дифференциала функции

ГОУ ВПО «Ярославская медицинская академия»

 

«Пособие по математическому анализу для студентов лечебного и педиатрического факультетов медицинской академии»

Ярославль

2009

Содержание.

Введение.

1. Множество и функция.

2. Производная функции.

3. Неопределенный интеграл.

4. Определенный интеграл.

5. Обыкновенные дифференциальные уравнения.

6 Литература.

7. Приложение. Сборник задач по производным, интегралам, дифференциальным уравнениям.

 

Введение.

 

Данное пособие написано на основании многолетнего опыта преподавания основ математического анализа студентам лечебного и педиатрического факультетов медицинской академии. В процессе обучения студенты, получив необходимые теоретические знания о дифференциальном и интегральном исчислении, учатся дифференцировать простые и сложные функции, находить определенные и неопределенные интегралы, решать простые дифференциальные уравнения.

Пособие соответствует учебному плану проведения занятий по математическому анализу для студентов первого курса лечебного и педиатрического факультетов и состоит из двух частей. Теоретическая часть содержит минимальный объем сведений для понимания основных понятий математического анализа. Практическая часть представляет собой сборник задач в который вошло около двухсот примеров.

Студентам данная работа поможет глубже понять вопросы, которые изучались на семинарах. Для развития умения решать практические задачи в пособии приведено и разобрано много примеров. Преподавателям в данном пособии предлагается большое количество задач для семинаров и домашних заданий.

При написании данной работы были учтены замечания и пожелания как коллег-преподавателей так и студентов. Данное пособие имеет электронную версию, поэтому необходимые исправления в него вносятся в минимальные сроки. Все замечания по данной работе направлять автору на электронный ящик

bobiskola@mail.ru.

 

 

1. Множество и функция.

Понятия множества и функции относятся к первичным понятиям математики как понятия точки или линии.

Множество — это совокупность конечного или бесконечного числа элементов, объединенных по какому-либо признаку. Множество называется числовым, если элементами множества являются числа. Некоторые числовые множества и их обозначения:

N - множество всех натуральных чисел;

Z - множество всех целых чисел;

R - множество всех действительных чисел.

Отношение между двумя множествами называется отображением, если каждому элементу одного множества соответствует только один элемент другого.

Числовой функцией называется отображение f числового множества X на множество R действительных чисел. Множество f называется областью определения функции f, а множество значений X —область допустимых значений функцииf.

D(f) - область определения функции (множество Х)

E(f) - множество значений функции (множество f)

Производная функции.

 

2.1 Определение производной функции одной переменной.

Пусть на некотором отрезке X=[a;b] определена функция f(x). Возьмем любую точку х Î Х и зададим аргументу х в данной точке произвольное приращение ∆х такое, что точка х +∆х так же принадлежит Х. Этим значениям аргумента х и х+∆х соответствуют следующие значения функции:

y(х) = f(х)

у(х+∆х) = f(х+∆х).

Приращение аргумента равно ∆х.

Приращение функции ∆y = f(х+∆х)-f(х).

Производной функции f(х) в точке х называется предел отношения приращения ∆y функции к при­ращению аргумента ∆х, когда приращение аргумента стремится к нулю:

=

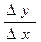
Для обозначения производной функции используют символ

y '(х) или f ′(х).

 

Читается: y'(х) - «иг­рек штрих по х»,

f '(х) - «эф штрих по х».

Таким образом, по определению:

f ′(х) = =

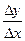Замечание 1: Предел

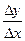должен существовать (т.е. быть конечным), только тогда можно говорить, что функция имеет производную в данной точке.

Случай, когда 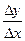= ∞ в данной работе не рассматривается.

Замечание 2: ∆y и ∆х — это единые символы, поэтому в выражении на ∆ сократить нельзя.

Процесс нахождения производной называется диффе­ренцированием функции. Функция называется дифферен­цируемойв точке х, если ее приращение можно представить в виде:

 

∆y=y'∆х + αΔх,

где y' – производная функции f(х) в точке х,

α = α(х) —бесконечно малая при Δх→0, т.е.

 

lim α = 0

^Dx®0

Дифференциалом функции y = f(х) в точке х называ­ется главная часть приращения функции в этой точке

 

dy = f'΄(х)Δх.

 

Дифференциалом независимой переменной х по определению считается величина: dх=Δх. Тогда дифференцил функции равен

 

dy = f΄(х)dх.

 

Таким образом:

 

 

Из данной формулы следует другое определение производной:

 

производная есть отношение дифференциала функции

1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: