 |
Основные методы интегрирования.
|
|
|
|
Нахождение неопределенного интеграла – сложная математическая задача, нет единого универсального метода, который позволил бы решить данную задачу. По алгебраическому виду интеграла его можно отнести к определенному классу интегралов, для которых метод нахождения неопределенного интеграла разработан. Хотя существует много различных методов интегрирования, все они основаны на преобразовании (приведении) первоначального интеграла к табличному виду. Рассмотрим некоторые из простых методов.
Метод интегрирования по формулам.
Способ нахождения неопределенных интегралов методом непосредственного использования таблицы интегралов в литературе по математическому анализу имеет несколько названий: непосредственное интегрирование, метод тождественных преобразований, метод интегрирования по формулам. Как правило, для того, чтобы привести интеграл к табличному виду, с первоначальным интегралом òf(x)dx необходимо проделать несложные тождественные преобразования.
Приведем несколько примеров.
1. ò(3cos x + 4x3 – ex )dx = ò3cos x dx + ò4x3 dx - òex dx = 3sin x + x4 - ex +C
2. 
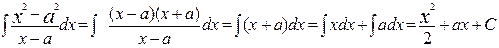
3. 
= 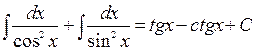
Правильность интегрирования проверяется дифференцированием найденного неопределенного интеграла. Производная должна быть равна подитегральной функции. Проверка основана на свойстве равенства
F¢(x) = f(x).
Метод замены переменных.
В некоторых случаях введение новой переменной интегрирования
x = j(t) позволяет свести неопределенный интеграл
òf(x)dx (1)
к табличному виду. Такой метод называется методом подстановки или методом замены переменной.
Алгоритм метода замены переменной для неопределенного интеграла следующий:
|
|
|
1. Введем новую переменную x = j(t) которая должна свести интеграл (1) к табличному виду. Решая данное уравнение относительно t имеем:
t = ψ(x)
2. В первоначальном интеграле (1) сделаем замену переменных:
f (x)= 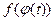
dx = j¢(t)dt
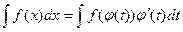 (2)
(2)
3. Интеграл (2) должен решаться в силу основного свойства подстановки x = j(t): данная подстановка должна сводить первоначальный интеграл к табличному виду. Решение интеграла (2) имеет следующий вид:
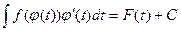 (3)
(3)
4. В интеграле (3) сделаем замену переменных t = ψ(x), то есть возвращаемся к первоначальной переменной х:
F(t) + C = F(ψ(x)) + C (4)
Для того, чтобы убедиться в том, что найденный интеграл (4) найден правильно, можно продифференцировать выражение (4) и сравнить с подинтегральной функцией интеграла (1). Подинтегральная функция f(x) должна совпадать с производной F¢(ψ(x)):
F¢(ψ(x)) = f(x).
3.4.3. Примеры нахождения неопределенного интеграла.
В данном примере один и тот же интеграл решен двумя разновидностями метода подстановки.
Найти неопределенный интеграл 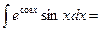
1 способ.
1. 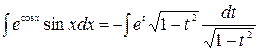 = -
= - 
1.1. Делаем замену переменных: t = cos x
1.2. Выражаем старую переменную через новую: x = arccos t
1.3. По определению дифференциала:
dx = j¢(t)dt = (arccos t)′ dt = 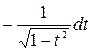
dx= 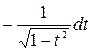
1.4. sin2x + cos2x = 1, т.к. t = cos x, то sin2x + t2 = 1,
sin x = 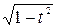
1.5. Заменяем в первоначальном интеграле cos x, sin x, dx через t.
1.6. Первоначальный интеграл свелся к табличному относительно t. Найти интеграл относительно t.
1.7. При использовании метода подстановки надо помнить, что после взятия неопределенного интеграла необходимо возвращаться от новой переменной t к первоначальной переменной x. Возвращаемся от переменной t к переменной х.
2 способ.
2. 
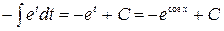
2.1. Вводим переменную t = cos x
2.2. Берем дифференциал от обеих частей и находим dx:
dt = - sin x dx
sin x dx = - dt
dx = - dt / sin x
2.3. Подставляем вместо cos x и dx их выражения через t в первоначальный интеграл и сводим его к табличному.
|
|
|
Определенный интеграл.
|
|
|


