 |
К дифференциалу аргумента.
|
|
|
|
Формула для дифференциала функции очень важна при взятии интегралов, приближенного вычисления функции в данной точке и решении дифференциальных уравнений.
Геометрический смысл производной.
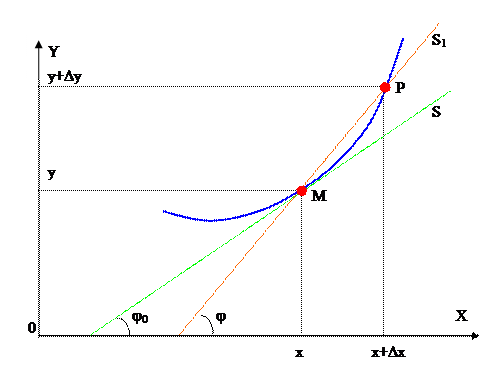
Пусть функция y=f(х) определена на отрезке X=[a;b] и пусть точка М на графике функции соответствует значению аргумента х, а точка Р значению х+∆х (смотри Рис.1). Проведем через точку М и Р прямую и назовем ее секущей (S1). Значение функции в точках М и Р
равно f(х) и f(х+∆х) соответственно. Из рассмотрения Рис. 1 видно, что тангенс угла наклона секущей S1 равен
Касательной S к графику функции y=f(х) в точке М (х;у) будем называть предельное положение секущейМР(S1) при Р→М‚ т.е. при Δх→0.
 |
f(x+Dx)
f(x)
Рис. 1.
Производная функции y=f(х) в точке х равна угловому коэффициенту касательной к графику функции y=f(х) в точке М (х;f(х)) = М(х,y):
f'΄(х) = tg φ0 = 
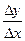
Физический смысл производной.
Пусть функция s=s(t) описывает закон движения материальной точки М по прямой траектории, т.е. s=s(t) — путь, пройденный точкой М от начала отсчета за время t. Тогда путь, пройденный М за время t + ∆t равен f(t + ∆t). За промежуток времени ∆t тело М пройдет путь, равный
∆s= s(t + ∆t) —s(t).
Средняя скорость Vср. движения точки М на отрезке ∆у за время ∆t равна:
Vср= ∆s/∆t.
Предел данного отношения при ∆t→ 0 называется мгновенной скоростью движения тела М в момент времени t:
По определению это и есть производная функции s=s(t) в точке t, т. е. производная функции s=s(t) в момент времени t есть мгновенная скорость тела М в данной точке.
Производная сложной функции.
До сих пор при нахождении производной предполагалось, что производная находится для функции у=f(х), где аргумент х—простая независимая переменная. Однако, в свою очередь, x может быть какой-то функцией, т.е. х = φ(t). Требуется найти производную такой сложной «двухэтажной» функции у=f[φ(t)] по аргументу t.
|
|
|
Докажем следующее правило для нахождения производной сложной функции у = f[φ(t)]:
у't=f'′x ∙ φ't
Доказательство.
По определению нахождения производной:
Уt' = lim f[φ(t+ ∆ t)] — f[φ(t)]
Δt→0 ∆ t
Умножим и разделим числитель и знаменатель на выражение φ(t+∆t) — φ(t) и перегруппируем сомножители числителя и знаменателя:
Уt' = lim f[φ(t+ ∆ t)] — f[φ(t)] φ(t+∆t) — φ(t) =
Δt→0 ∆ tφ(t+∆t) — φ(t)
= lim f[φ(t+ ∆ t)] — f[φ(t)] φ(t+∆t) — φ(t) =
Δt→0 φ(t+∆t) — φ(t) ∆ t
= f'′x ∙ φ't
Теорема доказана.
В данной теореме рассмотрена сложная функция, где у зависит от х через промежуточную элементарную функцию φ. Возможна и более сложная зависимость с двумя, тремя и большим числом промежуточных переменных каждая из которых элементарная функция. Однако правило дифференцирования остается таким же.
Пусть, например, у = f(х), где х=φ(u),u=ψ(v), v=λ(t). Тогда
У't= f'′х (х) φ'U(u) ψ'V(v) λ't(t).
Таблица производных
Элементарных функций.
Пользоваться определением производной функции для нахождения производной есть процедура, которая требует большого количества времени. Поэтому производные всех элементарных функции были найдены и сведены в таблицу. Таблица производных элементарных функций есть в любом учебнике по высшей математике, поэтому в данном пособии она приведена в качестве иллюстрации в небольшом объеме.
| Функция f(х) | Производная f'′(х) |
| f(х)=С С=const | |
| f(х)=хn | nxn—1 |
| f(х)=eх | ех |
| f(х)=aх | aх lna |
| f(х)=ln х | 1/x |
| f(х)=sin x | cos x |
| f(х)=cos x | - sin x |
| f(х)=tg x | 1/cos2 x |
| f(х)=ctg x | -1/sin2 x |
| f(х)=arcsin x | 1/ 
|
| f(х)=arccos x | - 1/
|
| f(х)=arctg x | 1/(1+x2) |
| f(х)=arcctg x | -1/(1+x2) |
|
|
|
На практике приходится дифференцировать алгебраические комбинации элементарных математических функций. Рассмотрим правила дифференцирования для двух простых функций U(х) и V(х):
(U+V)' = U'+V',
(UV)' = U'V+UV',
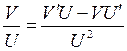
Примеры дифференцирования простых и сложных функций.
1. Y = х3 у'=3х2
2. Y = sin2x y´= cos2x(2x)΄ = 2cos2x
3. Y = sin32x y´=3sin 
2x(sin2x)΄ = 3sin 2xcos2x(2x)΄= 3sin 2xcos2x(2)= 6sin 2xcos2x = 3sin2xsin4x
4. Y= xx у′= (xx) = (exlnx) = exlnx(lnx+1).
Приближенное значение функции при малых
Значениях аргумента.
Приращение функции приблизительно равно дифференциалу функции, если приращение аргумента ∆x достаточно мало:
∆у = f(х+∆х)—f(х) ≈ dy ≈ f '(х)∆х.
Приближенное вычисление значения функции равно:
f(х+∆х) ≈ f(х)+f '(х)∆х.
В близи нуля (х=0) можно записать:
f(∆х) ≈ f(0)+f '(0)∆х.
Заменяя ∆x на x имеем: f(х) ≈ f(0) +f '(0)х.
В качестве примера рассмотрим функцию у=(1+х)1/2.
Вблизи нуля имеем:
y = у(0)+у'(0)х = (1+х)1/2 |x=0 +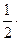 
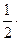= 1 + х
|
|
|
