 |
уравнений методом разделения переменных.
|
|
|
|
Рассмотрим последовательность следующих дифференциальных уравнений первого порядка в порядке их усложнения.
Левая часть у них есть производная y΄, а правая есть последовательность из комбинаций х и у, величина к есть константа.
y΄= 0, к, кх, ку, кху, k´y/x, ……
Все вышеприведенные дифференциальные уравнения решаются методом разделения переменных.
1. dy/dx = 0 (y¢ = 0)
y = C - константа
2. dy/dx = k (y¢ = k)
dy = kdx
òdy = òkdx = kòdx
y = kx+С
3. dy /dx = kx (y¢ = kx)
dy = kxdx
òdy = òkxdx = kòxdx
y = k´x2/2 +C
4. dy/dx = ky (y¢ = ky)
dy/y = kdx
òdy/y = òkdx = kòdx
ln y = kx+d
y = Cekx
5. dy/dx = kxy (y¢ = kxy)
dy/y = kxdx
òdy/y = òkxdx = kòxdx
ln y = k´xÙ2/2+C
y = e kxÙ2/2´e C = Ce kxÙ2/2
6. dy/dx = k´y/x (y¢ = k´y/x)
dy/y = k´dx/x
ln y = kln x + C
e ln y = e klnx +C = eC´elnxk
y = Cxk
7. (Öxy-2Öx)´ y¢-y = 0
Öx(Öy-2)dy/dx = y
(Öy-2)/y´dy = dx/Öx
dy/Öy -2dy/y = dx/Öx
òdy/Öy-2òdy/y = òdx/Öx
òy -0,5-2òdy/y = òx-0,5 dx
y 0,5/0,5 -2ln y = x0,5/0,5+C
2Öy-2ln y = 2Öx +C
Öy-ln y = Öx +C – общее решение
8. 
(1)
- неопределенный интеграл есть решение дифференциального уравнения (1)
Литература.
Основная литература.
1. И.И. Баврин, «Курс высшей математики», М, «Просвещение»,1992г.
2. А.Н. Ремизов, Н.Х. Исакова, «Сборник задач по физике», М, «Высшая школа», 1978г.
Дополнительная литература.
1. В.С. Щипачев, «Высшая математика», М, «Высшая школа»,1996г
2. Я.Б. Зельдович, А.Д. Мишкис, «Элементы прикладной математики», М, «Наука», 1967г.
3. В.А. Подольский, А.М. Суходольский, «Сборник задач по математике», М, «Высшая школа», 1978г.
Приложение.
Сборник задач
По производным, интегралам, дифференциальным уравнениям. Пособие для студентов медицинской академии.
|
|
|
I. Производная функции.
1. Найти производные следующих простых функций.
1.1. y = x3 + 4x2 +5 { y΄ = 3x2 + 8x }
1.2. 
{ y΄ = 3ax3 }
1.3. y = 
{ y΄ = 
}
1.4. 
{ 
}
1.5.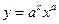 
{ 
}
1.6. 
{ 
}
1.7. 
{ 
}
1.8. 
{ 
}
1.9. 
{ 
}
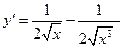1.10.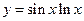 
{ 
}
1.11.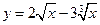 
{ 
}
1.12. 
{ 
}
1.13.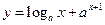 
{ 
}
1.14. 
{ 
}
1.15. 
{ 
}
1.16. 
{ 
}
1.17. 
{ 
}
1.18. 
{ 
}
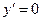1.19. 
{ 
}
1.20. 
{ 
}
1.21.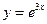 
{ 
}
1.22.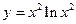 
{ 
}
1.23. 
{ 
}
1.24.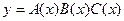 
{ 
}
1.25. 
{ 
}
1.26. 
{ 
}
1.27. 
{ }
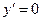1.28. 
{ 
}
1.29. 
{ 
}
1.30. 
{ 
}
2. Найти производные следующих сложных функций.
2.1. 
{ 
}
2.2. 
{ 
}
2.3. 
{ 
}
2.4. 
{ 
}
2.5.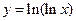 
{ 
}
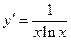2.6. 
{ 
}
2.7. 
{ 
}
2.8. 
{ 
}
2.9. 
{ 
}
2.10. 
{ 
}
2.11. 
{ 
}
2.12. 
{ 
}
2.13. 
{ 
}
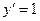2.14. 
{ 
}
2.15. 
{ 
}
2.16. 
{ 
}
2.17. 
{ 
}
2.18. 
{ 
}
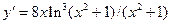2.19. 
{ 
}
2.20. 
{ 
}
2.21. 
{ 
}
2.22. 
{ 
}
2.23. 
{ 
}
2.24. 
{ 
}
2.25. 
{ 
}
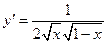2.26. 
{ 
}
2.27.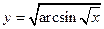 
{ 
}
2.28. 
{ 
}
2.29. 
{ 
}
2.30. 
{ 
}
I. Интегралы.
1. Найти неопределенные интегралы методом тождественных преобразований.
3.1. 
{ 
}
3.2. 
{ 
}
3.3. 
{ 
}
3.4. 
{ 
}
3.5.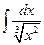 
{ 
}
3.6.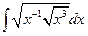 
{ 
}
3.7. 
{ 
}
3.8. 
{ 
}
3.9. 
{ 
}
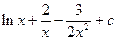3.10. 
{ 
}
3.11. 
{ 
}
3.12. 
{ 
}
3.13. 
{ 
}
3.14.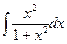 
{ 
}
3.15. 
{ 
}
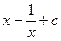3.16. 
{ 
}
3.17. 
{ 
}
3.18.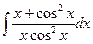 
{ 
}
3.19. 
{ 
}
3.20. 
{ 
}
3.21. 
{ 
}
3.22. 
{ 
}
3.23. 
{ 
}
3.24. 
{ 
}
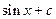3.25. 
{ 
}
3.26. 
{ 
}
3.27. 
{ 
}
3.28. 
{ 
}
3.29. 
{ 
}
3.30. 
{ }
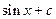II. Решить неопределенные интегралы методом замены переменной.
4.1. 
{ 
}
4.2. 
{ 
}
4.3. 
{ 
}
4.4.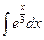 
{ 
}
4.5. 
{ 
}
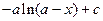4.6. 
{ 
}
4.7. 
{ 
}
4.8. 
{ 
}
4.9. 
{ 
}
4.10. 
{ 
}
4.11. 
{ 
}
4.12. 
{ 
}
4.13. 
{ 
}
4.14. 
{ 
}
4.15. 
{ 
}
4.16. 
{ 
}
4.17.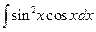 
{ 
}
4.18. 
{ 
}
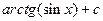4.19. 
{ 
}
4.20. 
{ 
}
4.21.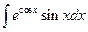 
{ 
}
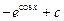4.22 
{ 
}
4.23. 
{ 
}
4.24. 
{ 
}
4.25. 
{ 
}
4.26. 
{ 
}
4.27. 
{ 
}
4.28. 
{ 
}
4.29. 
{ 
}
4.30. 
{ 
}
V. Найти определенный интеграл табличным методом, нарисовать геометрические фигуры, площадям которых соответствует данный определенный интеграл.
|
|
|
5.1. 
{ 
}
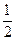5.2. 
{ 
}
5.3.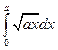 
{ 
}
5.4. 
{ 2 }
5.5. 
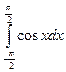{ 2 }
VI. Решить определенные интегралы методом замены переменной.
6.1.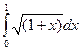 
{ 
}
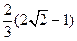6.2. 
{ 2 }
6.3. 
{ 
}
6.4. 
{ 1 }
6.5. 
{ 
}
6.6. 
{ 1 }
6.7. 
{ }
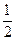6.8. 
{ 
}
6.9.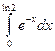 
{ }
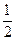6.10. 
{ 
}
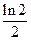6.11. 
{ 
}
6.12. 
{ 
}
6.13. 
{ }
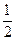6.14. 
{ 
}
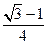6.15. 
{ 
}
6.16. 
{ 
}
6.17. 
{ 
}
6.18.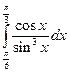 
{ 
}
6.19. 
{ }
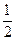6.20. 
{ 
}
6.21. 
{ }
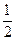6.22. 
{ 
}
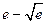6.23. 
{ }
6.24. 
{ 1 }
6.25. 
{ 14 }
6.26. 
{ 
}
6.27.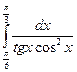 
{ 
}
6.28. 
{ 
}
6.29. 
{ 
}
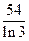6.30. 
{ 
}
VI. Найти общее решение дифференциальных уравнений первого порядка методом разделения переменных.
7.1. 
{ 
}
7.2. 
{ 
}
7.3. 
{ 
}
7.4.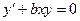 
{ 
}
7.5. 
{ 
}
7.6. 
{ 
}
7.7. 
{ 
}
7.8. 
{ 
}
7.9.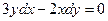 
{ 
}
7.10. 
{ 
}
7.11. 
{ 
}
7.12. 
{ 
}
7.13. 
{ 
}
7.14. 
{ 
}
7.15. 
{ 
}
VII. Найти частные решения дифференциальных уравнений первого порядка методом разделения переменных.
8.1. 
{ 
}
8.2. 
{ 
}
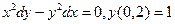8.3. 
{ 
}
8.4. 
{ 
}
8.5.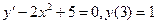 
{ 
}
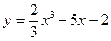8.6. 
{ 
}
8.7. 
{ 
}
8.8. 
{ 
}
8.9. 
{ 
}
8.10. 
{ 
}
8.11. 
{ 
}
8.12. 
{ 
}
8.13. 
{ 
}
8.14. 
{ 
}
8.15. 
{ 
}
|
|
|
