Система аксиом (П.С. Новиков).

Система аксиом (П. С. Новиков).

I   a1. A → (B → A);

    a2. (A → (B→ С)) → ((A → B) → (A → C));

II  a3. A & B → A;

    a4. A & B → B;

    a5. (A → B) → ((A → C) → (A → B & C));

III a6. A → A Ú B;

    a7. B → A Ú B;

    a8. (А → C) → ((B→ C) → (A Ú B → C));

IV a9. (A → B) → (B → A);

    a10. A → A;

    а11. A → A.

Все аксиомы – общезначимые ППФ.

Правила вывода.

Правило 1. Все аксиомы выводимы.

Правило 2. Правило подстановки. Пусть А – ППФ, содержащая атом X.

Тогда, если A – теорема исчисления высказываний, то заменив в ней атом X всюду, куда он входит, на произвольную ППФ В, мы получим также теорему. Сокращенно обозначим это правило через ПС. В принципе, считая, что каждая аксиома понимается как схе­ма аксиом, т. е. включает в себя бесконечно много аксиом, это пра­вило излишне. Мы оставим его ввиду наглядности и ясности изложения.

Правило 3. Правило modus ponens (правило дедуктивного вывода). Если А и А → В – теоремы, то В – также теорема. Это правило будем сокращенно обозначать через МР.

Правило 4. Других правил вывода нет.

Система аксиом исчисления высказывания обладает следующи­ми тремя важными свойствами: полнотой в широком и в узком смысле, непротиворечивостью и независимостью. Тот факт, что любая теорема ФС₁, является обще­значимой ППФ, вытекает из того, что все аксиомы – тавтологии и правила вывода, примененные к тавтологиям, всегда приводят к тавтологиям. Обратное утверждение и представляет собой теоре­му о полноте.

Теорема 1 (о полноте в широком смысле). Если ППФ А фор­мальной системы ФС₁ является общезначимой, то она есть теорема этой системы.

Кроме понятия полноты в широком смысле имеет место понятие полноты логического исчисления в узком смысле. Исчисление вы­сказываний называется полным в узком смысле, если присоедине­ние к его аксиомам какой-нибудь не выводимой в нем ППФ приво­дит к противоречию.

Перейдем ко второму свойству системы аксиом – непротиворе­чивости. Проблема непротиворечивости является одной из карди­нальных проблем математической логики.

Любое логическое исчисление называется непротиворечивым, если в нем не выводимы никакие две ППФ, из которых одна явля­ется отрицанием другой. Если мы имеем противоречивую систему, то в ней мы могли бы вывести любые ППФ, что не представляло бы никакой ценности, так как в такой системе не было бы разли­чий между истиной и ложью.

Например, известно, что следующая ППФ есть теорема, т. е. ├ A→ (A → B) и если в противоречивой системе некоторая ППФ А была бы выводима вместе со своим отрицанием А, то по пра­вилу МР была бы теоремой любая ППФ В.

Теорема 2 (о непротиворечивости). Исчисление высказываний непротиворечиво.

И наконец, третье свойство системы аксиом – независимость. Аксиома, не выводимая с помощью правил вывода из остальных аксиом, называется независимой от этих аксиом, а система аксиом, в которой ни одна аксиома не выводима из остальных, называется независимой системой аксиом.

Теорема 3 (о независимости). Каждая аксиома формальной системы ФС₁независима.

В заключение этого раздела заметим, что с помощью теоремы о полноте устанавливается факт равноценности понятия общезна­чимости и доказуемости. Так как вопрос об общезначимости может быть эффективно решен для произвольной ППФ, то понятие теоре­мы в исчислении высказываний эффективно.

 

 

Лекция 5. Исчисление предикатов

1. Понятие предиката

2. Кванторы. Двойственность.

3. Формулы исчисления предикатов

3. ИП как ФС

 

 

Понятие предиката.

В математике и других науках наряду с высказываниями встречаются выражения, имеющие форму высказывания, но содержащие переменные, принадлежащие некоторому множеству D. Множество называется предметной областью, а переменные – предметными переменными.

Например,

“2 – простое число” - высказывание;
“3> 1” - высказывание.

Но, заменив числа в этих высказываниях предметной переменной n из множества натуральных чисел, получим выражения:

“n - простое число”,
“n₁> n₂”,
являющиеся не высказываниями, а предикатами. Предикаты отражают свойства и отношения между предметами из предметной области.
Обозначим

P₁(n) - свойство “быть простым числом”, а
P₂(n₁, n₂) отношение “n₁ больше n₂”.

В общем случае мы ничего не можем сказать о значении предиката, но подставив, например, в P₁ и P₂ значения n=2, n₁=3, n₂=1, получим

P₁(2) - “2-простое число”,
P₂(3, 1) - “3 больше 1” -

истинные высказывания, а подставив значения n=4, n₁=1, n₂=3. получим

P₁(4) - “4 – простое число”,
P₂(1, 3) - “1 больше 3” –

ложные высказывания, т. е. предикат при подстановки конкретных констант из предметной области, может принимать значение И или Л.

Кванторы. Двойственность.

" - квантор всеобщности;
$ - квантор существования.

Если P(x) - одноместный предикат, то запись (" x)P(x) означает, что свойство P выполняется для всех предметов из предметной области, а
($ x)P(x) означает, что существует по крайней мере один предмет, обладающий свойством P.
Переход от P(x) к (" x)P(x) или к ($ x)P(x) называется связыванием переменной или навешиванием квантора на переменную x. Переменная, на которую навесили квантор, называется связанной, несвязанная переменная называется свободной.
Смысл связанных и свободных переменных различен. Свободная переменная – это переменная, которая может принимать любые значения из D. При этом P(x) зависит от значения x. Выражение (" x)P(x) от x не зависит и при заданных P и D имеет вполне определенное значение.
Например, если
P(x) - “быть четным числом”, то (" x)P(x) принимает значение Л, если D - множество натуральных чисел и (" x)P(x) принимает значение И, если D={2, 4, 6, …}.
Навешивание квантора на многоместный предикат уменьшает в нем число свободных переменных и превращает его в предикат от меньшего числа переменных.

Самое распространенное и часто применяемое свойство кванторов — это закон двойственности, который формулируется так:

1)

2)

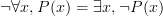
⇐ Предыдущая6789101112131415Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: