Формулы исчисления предикатов.

Формулы исчисления предикатов.

Для логики предикатов определим понятия терма, атома и формулы. Здесь мы имеем:

         х₁, х₂, …, х_n, … – предметные переменные;

         a₁, a₂, …a_k, … – предметные константы;

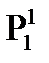         , , …, , …, , … – предикатные буквы;

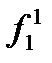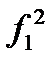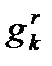         , , …, , …, , … – функциональные буквы.

Верхний индекс предикатной или функциональной буквы указывает число аргументов, а нижний служит для различения букв с одним и тем же числом аргументов. В дальнейшем верхний индекс будем опускать.

Правила конструирования термов:

1. всякая предметная переменная или предметная константа есть терм;

2. если f_i – функциональная буква и t₁, t₂, …, t_n – термы, то f_i(t₁, t₂, …, t_n) – терм;

3. других правил образования термов нет.

Например, х, у и 1 – термы, mult и plus – двухместные функциональные символы, тогда plus(y, 1) и mult(x, plus(y, 1)) – также термы.

Правила образования атомов (атомарных формул):

1. всякое переменное высказывание Х есть атом;

2. если P_i – предикатная буква, а t₁, t₂, …, t_n – термы, то P_i(t₁, t₂, …, t_n) есть атом;

3. других правил образования атомов нет.

Формулы логики предикатов конструируются по следующим правилам:

1. всякий атом есть формула;

2. если А и В – формулы и х – предметная переменная, то каждое из выражений Ø А, А & В, А Ú В, А ® В, А « В, " хА и $хА есть формула;

3. других правил образования формул нет.

Для того чтобы сократить количество скобок в формуле, используем правила силы операций:

1. связка Ø сильнее связок &, Ú, ®, «;

2. связка & сильнее связок Ú, ®, «;

3. связка Ú сильнее связок ®, «;

4. связка ® сильнее связки «.

Внешние скобки всегда будем опускать и вообще везде, где не возникает двусмысленностей, будем пользоваться минимумом скобок. Кроме того, всегда предполагаем, что свободные и связанные переменные обозначены разными буквами, и если один квантор находится в области действия другого, то переменные, связанные этими кванторами, также обозначены разными буквами.

Пример 4. Пусть P(x) и N(x) обозначают соответственно «х есть положительное целое число» и «х есть натуральное число». Тогда утверждение «Всякое положительное целое число есть натуральное число. Число 5 есть положительное целое число. Следовательно, 5 есть натуральное число» будет записано на языке логики предикатов следующим образом:

" х (P(x) ® N(x))

    P(5)      

N(5)

Отметим, что для перевода предложений с русского языка на язык логики предикатов в общем случае не существует механических правил. В каждом отдельном случае нужно сначала установить, каков смысл переводимого предложения, а затем пытаться передать тот же смысл с помощью предикатов, кванторов и термов. Для иллюстрации того, что при переводе могут возникнуть трудности, приведем довольно несложные высказывания.

Пример 5.

1. Все люди – животные: " y (S(y) ® C(y)).

2. Следовательно, голова человека является головой животного:

" x ($y (S(y) & V(x, y)) ® $z (C(z) & V(x, z))).

Здесь S(x) – «х – человек»;

    C(x) – «х – животное»;

    V(x, y) – «х является головой у».

Если перевод первого высказывания довольно прост, то с переводом второго возникают сложности, связанные с определением его семантики.

 

Рассмотрим формальную аксиоматическую систему ФС₂ для ис­числения предикатов.

1. Исходными элементами ФС₂ являются:

а) счетное множество предметных переменных x₁, х₂,, …, х_n, . . .;

б) конечное (может быть и пустое) или счетное множество предметных констант a₁, a₂, …;

в) конечное (может быть и пустое) или счетное множество функциональных букв ;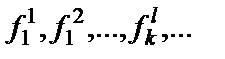

г) непустое конечное или счетное множество предикатных букв ;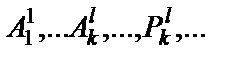

д) символы исчисления высказываний: , &, Ú, →;

е) скобки ( ) и запятая;

ж) символы ", $;

з) других исходных элементов нет.

2. Правила образования ППФ:

а) всякий атом есть ППФ;

б) если А и В – ППФ и х – предметная переменная, то каждое из выражений А, А → В, А & В, А Ú B, " х А и $х A есть ППФ;

в) других правил образования ППФ нет.

Таким образом, форма записи ППФ совпадает с записью фор­мул исчисления предикатов.

3. Система аксиом.

К системе аксиом исчисления высказываний добавляются еще две аксиомы:

a12. " x A(x)) → A(t), где A(x) есть ППФ и t – терм, свобод­ный для x в A(x).

а13. A(t) → $x A(x), где A(x) есть ППФ и t – терм, свобод­ный для x в A(x).

4. Правила вывода.

Правило 1. Все аксиомы выводимы.

Правило 2. Правило подстановки. Это правило аналогично правилу подстановки, которое имело место для исчисления высказываний. Только для ФС₂ мы будем иметь дело с такой подстановкой термов t₁, t₂, …, t_k вместо 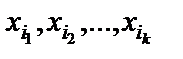 в A[ 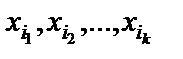], что A[ 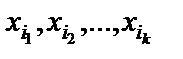] свободна для t₁, t₂, …, t_k.

Несоблюдение этого условия может привести к неприятным последствиям. Например, пусть в аксиоме 12 терм t не свободен для x в А[x] и пусть А[x] есть ППФ вида " x₂A(x₁, x₂) и t есть x₂. Тогда терм t не свободен для x₁ в " x₂A(x₁, x₂).

Рассмотрим а12: " x₁(" x₂ A(x₁, x₂)) → " ₂A(x₂, x₂).

Возьмем в качестве интерпретации любую область, содержащую не менее двух элементов, а в качестве A – отношение тождества. Тогда посылка " x₁(" x₂A(x₁, x₂)) в а12 истинна, а заключение " x₂ A(x₂, x₂) ложно.

Правило 3. Правило modus ponens (МР).

Если ├ A и ├ A → В, то ├ B.

Правило 4. Правило обобщения (или правило связывания квантором общности).

Если ППФ B → A(x) при условии, что В не содержит свобод­ных вхождении x, выводима, то выводима будет и ППФ B → " x A(x). В дальнейшем это правило будем обозначать че­рез Gen.

Правило 5. Правило конкретизации (или правило связывания кван­тором существования).

Если A(x) → В – выводимая ППФ (теорема) и В не содержит свободных вхождений x, то $x A(x) → В также теорема. Обоз­начим это правило через Еx.

Правило 6. Если A – теорема, имеющая квантор общности и/или кван­тор существования, то одна связанная переменная в A может быть заменена другой связанной переменной, отличной от всех свобод­ных переменных, одновременно во всех областях действия кванто­ра и в самом кванторе. Полученная ППФ также является теоремой.

Правило 7 . Других правил вывода нет.

Определение выводимости в исчислении предикатов является расширением соответствующего определения для исчисления выска­зываний. Поэтому среди выводимых ППФ исчисления предикатов будут находиться все выводимые ППФ исчисления высказываний.

Будем считать, что ППФ B выводима из ППФ A (аналогично из множества ППФ A₁, …, A_n), если:

1. A выводима из A;

2. каждая выводимая в ФС₂ ППФ также выводима и из A;

3. из выводимости ППФ B₁, и B₁ → B₂ из A следует выводимость B₂ из A;

4. если ППФ B₁ → B₂(x) выводима из A, причем B₁ и A не содержат свободных вхождений x, то и ППФ B₁ → " xB₂(x) также выводима из A;

5. если ППФ B₂(x) → B₁ выводима из A. причем B₁ и A не содержат свободных вхождений x, то и ППФ $хB₂(x) → B₁ выводима из A;

6. если ППФ B выводима из ППФ A, то и B', полученная из B подстановкой термов вместо свободных вхождений в B перемен­ных, также выводима из A;

7. если B выводима из A. то и B', полученная из B любым переименованием связанных переменных, отличных от имен сво­бодных переменных, выводима из A.

Вывод ППФ из пустого множества посылок есть доказательство этой ППФ. а сама ППФ называется теоремой.

Для исчисления предикатов также имеет место теорема дедук­ции: если A₁, A₂, …, A_n ├ B, то ├ A₁ → (A₂ → (…(A_n → B)…)).

Правила силлогизма, перестановки посылок, объединения и разъединения посылок для исчисления предикатов доказываются аналогично.

 

⇐ Предыдущая6789101112131415Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: