 |
Лекция 7. Доказательство логического следствия
|
|
|
|
1. Определение ЛС.
2. Две теоремы о ЛС.
3. ПНФ
4. ССФ
Как мы уже упоминали, исчисление предикатов первого порядка является примером неразрешимой формальной системы. В доказанной А. Чёрчем теореме говорится об отсутствии эффективной процедуры при решении вопроса относительно произвольной формулы исчисления предикатов первого порядка, является ли эта формула теоремой. Однако при доказательстве заключительного утверждения (цели) из начальной системы аксиом, посылок мы придерживаемся правила, что если все аксиомы и посылки принимают истинностное значение И, то и заключительное утверждение также принимает значение И. Из-за этого ограничения иногда исчисление предикатов первого порядка и называют полуразрешимым. Рассмотрим пример.
Пример 1. Горничная сказала, что она видела дворецкого в гостиной. Гостиная находится рядом с кухней. Выстрел раздался на кухне и мог быть услышан во всех близлежащих комната. Дворецкий, обладающий хорошим слухом, сказал, что он не слышал выстрела. Детектив должен доказать, что если горничная сказала правду, то дворецкий солгал.
1. P ® Q: если горничная сказала правду, то дворецкий был в гостиной.
2. Q ® R: если дворецкий был в гостиной, то он находился рядом с кухней.
3. R ® L: если дворецкий был рядом с кухней, то он слышал выстрел.
4. M ® Ø L: если дворецкий сказал правду, то он не слышал выстрела.
Требуется доказать, что если горничная сказала правду, то дворецкий солгал, т. е. P ® Ø M.
Представим посылки в КНФ: (Ø P Ú Q) & (Ø Q Ú R) & (Ø R Ú L) & (Ø M Ú Ø L).
Аналогично заключение: Ø P Ú Ø M.
Задавая интерпретации, в которых истинны посылки, нетрудно обнаружить, что будет истинно и заключение. Желающие могут выписать истинностную таблицу, чтобы в этом убедиться.
|
|
|
Таким образом, если даны формулы F1, F2, …, Fn и G, то говорят, что формула G является логическим следствием F1, F2, …, Fn (или G логически следует из F1, F2, …, Fn) тогда и только тогда, когда для любой интерпретации I, в которой F1 & F2 & … & Fn истинна, G также истинна.
Для обозначения логического следования формулы G из посылок F1, F2, …, Fn будем писать F1, F2, …, Fn ╞ G. Символ ╞ есть некоторое отношение между формулами, причем, если посылки соединены знаком &, то имеет место двуместное отношение: F1 & F2 & … & Fn ╞ G. Теперь приведем две простые, но важные теоремы, связывающие понятия логического следования с понятиями общезначимости и противоречивости.
Теорема 1 о логическом следствии. Даны формулы F1, F2, …, Fn и G. Формула G является логическим следствием формул F1, F2, …, Fn тогда и только тогда, когда формула F1 & F2 & … & Fn ® G общезначима, т. е. ╞ F1 & F2 & … & Fn ® G. Формула F1 & F2 & … & Fn ® G называется теоремой, а G называется заключением теоремы.
Теорема 2 о логическом следствии. Даны формулы F1, F2, …, Fn и G. Формула G является логическим следствием формул F1, F2, …, Fn тогда и только тогда, когда формула F1 & F2 & … & Fn & Ø G противоречива.
Таким образом, факт, что данная формула является логическим следствием конечной последовательности формул, сводится к доказательству общезначимости или противоречивости некоторой формулы. Следовательно, имеется полная аналогия при выводе заключения теоремы из множества аксиом или посылок в формальной системе, и многие проблемы в математике могут быть сформулированы как проблемы доказательства теорем.
Обозначим общезначимую формулу через ¢, а противоречивую – через £. Вернемся к примеру 1 (горничная и дворецкий), и покажем, что формула (Ø P Ú Q) & (Ø Q Ú R) & (Ø R Ú L) & (Ø M Ú Ø L) ® (Ø P Ú Ø M) общезначима.
|
|
|
Действительно, Ø [(Ø P Ú Q) & (Ø Q Ú R) & (Ø R Ú L) & (Ø M Ú Ø L)] Ú Ø P Ú Ø M =
= P & Ø Q Ú Q & Ø R Ú R & Ø L Ú M & L Ú Ø P Ú Ø M =
= Ø Q Ú Ø R Ú Ø L Ú M Ú Ø P Ú Ø M = ¢.
Аналогично можно показать противоречивость формулы (Ø P Ú Q) & (Ø Q Ú R) & (Ø R Ú L) & (Ø M Ú Ø L) & Ø (Ø P Ú Ø M) = £.
Аналогичный подход может быть использован и для логики предикатов. Рассмотрим пример 2:
Все люди – животные: " y (S(y) ® C(y)).
Следовательно, голова человека является головой животного:
" x ($y (S(y) & V(x, y)) ® $z (C(z) & V(x, z))).
Здесь S(x) – «х – человек»;
C(x) – «х – животное»;
V(x, y) – «х является головой у».
Покажем, что конъюнкция посылки и отрицания заключения есть противоречивая формула, т. е. " y (S(y) ® C(y)) & Ø " x ($y (S(y) & V(x, y)) ® $z (C(z) & V(x, z))) = £.
Для этого приведем ее к ССФ.
Посылка имеет вид: Ø S(y) Ú C(y).
Отрицание заключения: Ø " x (Ø $y (S(y) & V(x, y)) Ú $z (C(z) & V(x, z))) = Ø " x (" y(Ø S(y) Ú Ø V(x, y)) Ú $ z (C(z) & V(x, z))) = Ø " x" y$z (Ø S(y) Ú Ø V(x, y) Ú (C(z) & V(x, z))) = $x$y" z (S(y) & V(x, y) & (Ø C(z) Ú Ø V(x, z))) и ССФ имеет вид: S(b) & V(a, b) & (Ø C(z) Ú Ø V(a, z)).
Таким образом, (Ø S(b) Ú C(b)) & S(b) & V(a, b) & (Ø C(b) Ú Ø V(a, b)) = Ø S(b) & S(b) & V(a, b) & Ø C(b) Ú C(b) & S(b) & V(a, b) & Ø V(a, b) = £.
Примененный здесь подход для получения общезначимой (противоречивой) формулы, конечно, далек от практического применения. В дальнейшем будут даны более эффективные процедуры доказательства общезначимости или противоречивости формул.
В заключение отметим, что из двух теорем (1 и 2), как правило, применяется вторая теорема, т. е. если формула G является логическим следствием формул F1, F2, …, Fn, то надо доказать противоречивость формулы F1 & F2 & … & Fn & Ø G. Так как в этой формуле заключение теоремы G опровергается, то и процедуры поиска доказательства называются процедурами поиска опровержения, т. е. вместо доказательства общезначимости формулы доказывается, что отрицание формулы противоречиво. Потери общности нет.
|
|
|
В логике предикатов также имеется нормальная форма, называемая пренексной нормальной формой (ПНФ). Необходимость введения ПНФ будет обусловлена в дальнейшем упрощением процедуры доказательства теорем.
Сначала рассмотрим некоторые равносильные формулы в исчислении предикатов. Напомним, что две формулы F и Ф равносильные, т. е. F = Ф, тогда и только тогда, когда истинностные значения этих формул совпадают при любой интерпретации F и Ф. Для подчеркивания факта, что переменная х входит в формулу F, будем писать F[x], хотя F может содержать и другие переменные.
Имеем следующие пары равносильных формул:
" x F[x] Ú Ф = " x (F[x] Ú Ф);
" x F[x] & Ф = " x (F[x] & Ф);
$x F[x] Ú Ф = $x (F[x] Ú Ф);
$x F[x] & Ф = $x (F[x] & Ф)
при условии, что переменная х не входит свободно в формулу Ф. Равносильность этих формул очевидна, так как формула Ф не содержит свободно х потому не входит в область действия кванторов.
Далее имеем:
" x F[x] & " x Ф[x] = " x (F[x] & Ф[x]),
$x F[x] Ú $x Ф[x] = $ x (F[x] Ú Ф[x]).
Доказательство этих двух равносильностей оставляем читателю.
Однако " x F[x] Ú " x Ф[x] ¹ " x (F[x] Ú Ф[x]),
$x F[x] & $x Ф[x] ¹ $ x (F[x] & Ф[x]).
Действительно, взяв область интерпретации D = {1, 2} и положив при некоторой интерпретации F[1] = И и F[2] = Л, а Ф[1] = Л и Ф[2] = И, получим в левой части первого неравенства значение Л, а в правой – И. Аналогично доказывается и второе неравенство. В последних двух случаях производим переименование связанных переменных, т. е. " x F[x] Ú " x Ф[x] = " x F[x] Ú " у Ф[у] = " x " у (F[x] Ú Ф[у]), $x F[x] & $x Ф[x] = $x F[x] & $y Ф[y] = $x $y (F[x] & Ф[y]) при условии, что переменная у не появляется в F[x].
Теперь дадим определение ПНФ. Говорят, что формула F логики предикатов находится в ПНФ тогда и только тогда, когда ее можно представить в форме 
1х1 2х2 … rxr M, где ixi, i =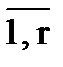 
, есть либо " xi, либо $xi и М – бескванторная формула. Иногда называют 1х1 2х2 … rxr префиксом, а М – матрицей формулы F.
Например, формула F1 = $x " y (Q(x, y) Ú P(f(x)) ® R(x, g(y))) находится в ПНФ, а формула F2 = " x (P(x) ® $y Q(x, y)) – не в ПНФ.
|
|
|
Существует алгоритм, преобразующий произвольную заданную формулу в равносильную ей формулу, имеющую пренексный вид. Алгоритм состоит из следующих шагов.
Шаг 1. Исключение логических связок « и ®. Многократно (пока это возможно) делаем замены: F « Ф = (Ø F Ú Ф) & (F Ú Ø Ф), F ® Ф = Ø F Ú Ф. Результатом этого шага будет формула, равносильная исходной и не содержащая связок « и ®.
Шаг 2. Продвижение знака отрицания Ø до атома. Многократно (пока это возможно) делаем замены:
Ø Ø F = F,
Ø (F Ú Ф) = Ø F & Ø Ф,
Ø (F & Ф) = Ø F Ú Ø Ф,
Ø " x F[x] = $x (Ø F[x]),
Ø $x F[x] = " x (Ø F[x]).
Очевидно, что в результате выполнения этого шага получается формула, у которой знаки отрицания Ø могут стоять лишь перед атомами.
Шаг 3. Переименование связанных переменных. Многократно (пока это возможно) применяется следующее правило: найти самое левое вхождение переменной такое, что это вхождение связано (некоторым квантором), но существует еще одно вхождение этой же переменной; затем сделать замену связанного вхождения на вхождение новой переменной.
Шаг 4. Вынесение кванторов. Для этого используем следующие равносильности:
x F[x] Ú Ф = x (F[x] Ú Ф),
x F[x] & Ф = x (F[x] & Ф),
" x F[x] & " x Ф[x] = " x (F[x] & Ф[x]),
$x F[x] Ú $x Ф[x] = $x (F[x Ú Ф[x]),
1x F[x] Ú 2x Ф [x] = 1x 2y (F[x] Ú Ф[y]),
1x F[x] & 2x Ф [x] = 1x 2y (F[x]& Ф[y]),
где , 1 и 2 – кванторы либо ", либо $.
После выполнения четвертого шага формула приобретает пренексный вид:
1х1 2х2 … rxr M, где i, {i = 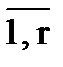} Î {", $}.
Таким образом, мы ограничимся формулами, имеющими пренексный вид.
Однако, можно рассматривать еще более узкий класс формул, так называемых " ‑ формул.
Формула F называется " ‑ формулой, если она представлена в ПНФ, причем кванторная часть состоит только из кванторов общности, т. е. F = " x1" x2…" xr M, где М – бескванторная формула.
Отсюда возникает задача устранения кванторов существования в формулах, представленных в ПНФ. Это можно сделать путем введения сколемовских функций.
Пусть формула F представлена в ПНФ.
F = 1х1 2х2 … rxr M, где j Î {", $}, , j = .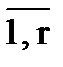
Пусть i (1 £ i £ r) – квантор существования в префиксе 1х1 2х2 … rxr. Если i = 1, т. е. ни один квантор общности не стоит впереди квантора существования, то выбираем константу с из области определения М, отличную от констант, встречающихся в М, и заменяем х1 на с в М. Из префикса квантор существования 1х1 вычеркиваем. Если перед квантором существования i стоит j1, j2, …, jm кванторов общности, то выбираем m-местный функциональный символ f, отличный от функциональных символов в М, и заменяем xi на f(xj1, xj2, …, xjm), называемую сколемовской функцией, в М. Квантор существования iхi вычеркиваем из префикса. Аналогично удаляются и другие кванторы существования в ПНФ. В итоге получаем " ‑ формулу. Опишем алгоритм последовательного исключения кванторов существования.
|
|
|
Алгоритм Сколема.
Шаг 1. Формулу представить в ПНФ.
Шаг 2. Найти наименьший индекс i такой, что 1, 2, …, i-1 все равны ", но i = $. Если i = 1, т. е. квантор $ стоит на первом месте, то вместо x1 в формулу М подставить константу с, отличную от констант, встречающихся в М, и квантор $ удалить из префикса. Если такого i нет, то СТОП: формула F является " -формулой.
Шаг 3. Взять новый (i – 1)-местный функциональный символ fi, не встречающийся в F. Заменить F на формулу " x1 " x2 … " xi‑ 1 i+1xi+1 … rxr M[x1, x2, …, xi‑ 1, fi(x1, x2, …, xi‑ 1), xi+1, …, xr].
Шаг 4. Перейти к шагу 2.
Пример 3. Пусть F = $x" y" z$u" v$w (P(x, y) Ú Ø R(z, u, v) & Q(u, w)). Применяя алгоритм Сколема, получаем следующую последовательность формул:
" y" z$u" v$w (P(с, y) Ú Ø R(z, u, v) & Q(u, w));
" y" z" v$w (P(с, y) Ú Ø R(z, f(y, z), v) & Q(f(y, z), w));
" y" z" v (P(с, y) Ú Ø R(z, f(y, z), v) & Q(f(y, z), g(y, z, v))).
Переход от формулы в пренексной форме к " -формуле не затрагивает свойство формулы быть невыполнимой (противоречивой). Это доказывается следующей теоремой.
Теорема 5. Пусть формула F задана в ПНФ и преобразована в " -формулу. Тогда F в пренексной форме логически невыполнима тогда и только тогда, когда невыполнима " -формула F.
Аналогичная теорема имеет место и для общезначимых формул. Однако следует заметить, что если имеется выполнимая формула F, то может оказаться, что " -формула для F будет невыполнимой. Действительно, пусть F = $x P(x) и соответствующая ей " -формула есть Р(с). Тогда, задавая область интерпретации D = {1, 2} и интерпретируя Р(1) = Л и Р(2) = И и положив с = 1, получаем, что F в пренексной форме выполнима, а " -формула невыполнима в этой интерпретации.
Таким образом, алгоритм Сколема, сохраняя свойство невыполнимости (противоречивости), приводит произвольную формулу, имеющую пренексный вид, к " -формуле.
|
|
|
