 |
Режим простой замены. Для реализации алгоритма шифрования данных в режиме простой замены используется только часть блоков общей криптосистемы.
|
|
|
|
Обозначения на схеме (рис. 24):
N1, N2 – 32-разрядные накопители;
СМ1 – 32-разрядный сумматор по модулю 232 (⊞);
СМ2 – 32-разрядный сумматор по модулю 2 (Å);
R – 32-разрядный регистр циклического сдвига;
КЗУ – ключевое запоминающее устройство на 256 бит, состоящее из восьми 32-разрядных накопителей Х0, Х1, Х2,..., Х7;
S – блок подстановки, состоящий из восьми узлов замены (S-блоков замены) S1, S2, S3,..., S7, S8.
Зашифрование открытых данных в режиме простой замены (рис.24). Открытые данные, подлежащие зашифрованию, разбивают на 64-разрядные блоки Т0. Процедура зашифрования 64-разрядного блока Т0 в режиме простой замены включает 32 цикла (j  {1,…,32}). В ключевое запоминающее устройство вводят 256 бит ключа К в виде восьми 32-разрядных подключей (чисел) Кi:
{1,…,32}). В ключевое запоминающее устройство вводят 256 бит ключа К в виде восьми 32-разрядных подключей (чисел) Кi:
К=К7К6К5К4К3К2К1К0.
Последовательность битов блока
Т0=(a1(0), a2(0),..., a31(0), a32(0), b1(0), b2(0),..., b31(0), b32(0))
разбивают на две последовательности по 32 бита: b(0) a(0), где b(0) – левые или старшие биты, a(0) – правые или младшие биты.

Рис. 24. Схема реализации режима простой замены
Эти последовательности вводят в накопители N1 и N2 перед началом первого цикла зашифрования. В результате начальное заполнение накопителя N1
a (0) = (a32(0), a31(0),..., a2(0), a1(0)),
32, 31,... 2, 1 номер разряда N1
начальное заполнение накопителя N2
b(0) = (b32(0), b31(0),..., b2(0), b1(0)).
32, 31,... 2, 1 номер разряда N2
Первый цикл (j=1) процедуры зашифрования 64-разрядного блока открытых данных можно описать уравнениями:
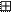

Здесь a (1) – заполнение N1 после 1-го цикла зашифровaния; b (1) – заполнение N2 после 1-го цикла зашифрования; f – функция шифрования.
Аргументом функции f является сумма по модулю 232 числа a(0) (начального заполнения накопителя N1) и числа К0 – подключа, считываемого из накопителя Х0 КЗУ. Каждое из этих чисел равно 32 битам. Функция f включает две операции над полученной 32-разрядной суммой (a (0) ⊞ К0).
|
|
|
Перваяоперация называется подстановкой (заменой) и выполняется блокомподстановкиS. Блок подстановки S состоит из восьми узлов замены (S-блоков замены) S1,S2,...,S8 с памятью 64 бит каждый. Поступающий из СМ1 на блок подстановки S 32-разрядный вектор разбивают на восемь последовательно идущих 4-разрядных векторов, каждый из которых преобразуется в четырехразрядный вектор соответствующим узлом замены. Каждый узел замены можно представить в виде таблицы-перестановки шестнадцати четырехразрядных двоичных чисел в диапазоне 0000…1111. Входной вектор указывает адрес строки в таблице, а число в этой строке является выходным вектором. Затем четырехразрядные выходные векторы последовательно объединяют в 32-разрядный вектор. Узлы замены (таблицы-перестановки) представляют собой ключевые элементы, которые являются общими для сети ЭВМ и редко изменяются. Эти узлы замены должны сохраняться в секрете.
Втораяоперация – циклический сдвиг влево (на 11 разрядов) 32-разрядного вектора, полученного с выхода блока подстановки S. Циклический сдвиг выполняется регистром сдвига R.
Далее результат работы функции шифрования f суммируют поразрядно по модулю 2 в сумматоре СМ2 с 32-разрядным начальным заполнением b(0) накопителя N2. Затем полученный на выходе СМ2 результат (значение a(1)) записывают в накопитель N1, а старое значение N1 (значение a(0)) переписывают в накопитель N2 (значение b(1) = a(0)). Первый цикл завершен.
Последующие циклы осуществляются аналогично, при этом во втором цикле из КЗУ считывают заполнение Х1 – подключ К1, в третьем цикле – подключ К2 и т.д., в восьмом цикле – подключ К7. В циклах с 9-го по 16-й, а также в циклах с 17-го по 24-й подключи из КЗУ считываются в том же порядке: К0, К1, К2,...,К6, К7. В последних восьми циклах с 25-го по 32-й порядок считывания подключей из КЗУ обратный: К7, К6,..., К2, К1, К0. Таким образом, при зашифровании в 32 циклах осуществляется следующий порядок выборки из КЗУ подключей:
|
|
|
К0, К1, К2, К3, К4, К5, К6, К7, К0, К1, К2, К3, К4, К5, К6, К7,
К0, К1, К2, К3, К4, К5, К6, К7, К7, К6, К5, К4, К3, К2, К1, К0.
В 32-м цикле результат из сумматора СМ2 вводится в накопитель N2, а в накопителе N1 сохраняется прежнее заполнение. Полученные после 32-го цикла зашифрования заполнения накопителей N1 и N2 являются блоком зашифрованных данных Тш, соответствующим блоку открытых данных Т0.
Уравнения зашифрования в режиме простой замены имеют вид:

 при j
при j  {1,…,24},
{1,…,24},

 при j
при j  {25,…,31},
{25,…,31},

 при j=32
при j=32
где a (j) = (a32(j), a31(j),..., a1(j)) – заполнение N1 после j-го цикла зашифрования;
b (j) = (b32(j), b31(j),..., b1(j)) – заполнение N2 после j-го цикла зашифрования, j  {1,…,32}.
{1,…,32}.
Блок зашифрованных данных Тш (64 разряда) выводится из накопителей N1, N2 в следующем порядке: из разрядов 1…32 накопителя N1, затем из разрядов 1…32 накопителя N2, т.е. начиная с младших разрядов:
Тш = (a1(32), a2(32),..., a32(32), b1(32), b2(32),..., b32(32)).
Остальные блоки открытых данных зашифровываются в режиме простой замены аналогично.
Расшифрование в режиме простой замены. Криптосхема, реализующая алгоритм расшифрования в режиме простой замены, имеет тот же вид, что и при зашифровании (см. рис. 24).
В КЗУ вводят 256 бит ключа, на котором осуществлялось зашифрование. Зашифрованные данные, подлежащие расшифрованию, разбиты на блоки Тш по 64 бита в каждом. Ввод любого блока
Тш = (a1(32), a2(32),..., a32(32), b1(32), b2(32),..., b32(32))
в накопители N1 и N2 производят так, чтобы начальное значение накопителя N1 имело вид
(a32(32), a31(32),..., a2(32), a1(32)),
32, 31,..., 2, 1 номер разряда N1
а начальное заполнение накопителя N2 – вид
(b32(32), b31(32),..., b2(32), b1(32)).
32, 31,..., 2, 1 номер разряда N2
Расшифрование осуществляется по тому же алгоритму, что и зашифрование, с тем изменением, что заполнения накопителей X0, Х1,..., Х7 считываются из КЗУ в циклах расшифрования в следующем порядке:
К0, К1, К2, К3, К4, К5, К6, К7, К7, К6, К5, К4, К3, К2, К1, К0,
К7, К6, К5, К4, К3, К2, К1, К0, К7, К6, К5, К4, К3, К2, К1, К0.
Уравнения расшифрования имеют вид:

 при j
при j  {1,…,8};
{1,…,8};
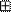
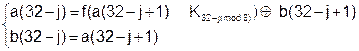 при j
при j  {9,…,31};
{9,…,31};

 при j=32.
при j=32.
Полученные после 32 циклов работы заполнения накопителей N1 и N2 образуют блок открытых данных
Т0 = (a1(0), a2(0),..., a32(0), b1(0), b2(0),..., b32(0)),
|
|
|
соответствующий блоку зашифрованных данных Тш. При этом состояние накопителя N1
(a32(0), a31(0),..., a2(0), a1(0)),
32, 31,..., 2, 1 номер разряда N1
состояние накопителя N2
(b32(0), b31(0),..., b2(0), b1(0)).
32, 31,..., 2, 1 номер разряда N2
Аналогично расшифровываются остальные блоки зашифрованных данных.
Если алгоритм зашифрования в режиме простой замены 64-битового блока Т0 обозначить через А, то
А(Т0) = А(a (0), b(0)) = (a (32), b(32))=Тш.
Следует иметь в виду, что режим простой замены допустимо использовать для шифрования данных только в ограниченных случаях – при выработке ключа и зашифровании его с обеспечением имитозащиты для передачи по каналам связи или для хранения в памяти ЭВМ.
Режим гаммирования.
Зашифрование открытых данных в режиме гаммирования. Криптосхема, реализующая алгоритм зашифрования в режиме гаммирования, показана на рис. 25. Открытые данные разбивают на 64-разрядные блоки
Т0(1), Т0(2),..., Т0(i),..., Т0(m),
где Т0(i) – i-й 64-разрядный блок открытых данных, i  {1,…,m}, m определяется объемом шифруемых данных.
{1,…,m}, m определяется объемом шифруемых данных.

Рис. 25. Схема реализации режима гаммирования
Эти блоки поочередно зашифровываются в режиме гаммирования путем поразрядного сложения по модулю 2 в сумматоре СМ5 с гаммой шифра Гш, которая вырабатывается блоками по 64 бита, т.е.
Гш=(Гш(1), Гш(2),..., Гш(i), Гш(m)),
где Гш(i) – i-й 64-разрядный блок, i  {1,…,m}.
{1,…,m}.
Число двоичных разрядов в блоке Т0(m) может быть меньше 64, при этом неиспользованная для зашифрования часть гаммы шифра из блока Гш(m) отбрасывается.
Уравнение зашифрования данных в режиме гаммирования имеет вид
Тш(i) = Т0(i) Å Гш(i),
где Гш(i)=А(Yi–1 ⊞ C2, Zi–1 ⊞´C1),i  {1,…,m}; Тш(i) – i-й блок 64-разрядного блока зашифрованного текста; А(·) – функция зашифрования в режиме простой замены; С1, С2 – 32-разрядные двоичные константы; Yi, Zi– 32-разрядные двоичные последовательности.
{1,…,m}; Тш(i) – i-й блок 64-разрядного блока зашифрованного текста; А(·) – функция зашифрования в режиме простой замены; С1, С2 – 32-разрядные двоичные константы; Yi, Zi– 32-разрядные двоичные последовательности.
Величины Yi, Zi определяются итерационно по мере формирования гаммы Гш следующим образом:
(Y0, Z0) = А (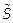 ),
),
где 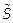 – синхропосылка (64-разрядная двоичная последовательность),
– синхропосылка (64-разрядная двоичная последовательность),
(Yi, Zi) = (Yi–1 ⊞ С2, Zi–1 ⊞ C1), i  {1,…,m}.
{1,…,m}.
Рассмотрим реализацию процедуры зашифрования в режиме гаммирования.
В накопители N6 и N5 заранее записаны 32-разрядные двоичные константы С1 и С2, имеющие следующие значения (в шестнадцатеричной форме):
|
|
|
С1 = 01010104(16), С2 = 01010101(16).
В КЗУ вводится 256 бит ключа; в накопители N1 и N2 – 64-разрядная двоичная последовательность (синхропосылка)
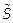 = (S1, S2,..., S64).
= (S1, S2,..., S64).
Синхропосылка 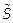 является исходным заполнением накопителей N1 и N2 для последовательной выработки m блоков гаммы шифра.
является исходным заполнением накопителей N1 и N2 для последовательной выработки m блоков гаммы шифра.
Исходное заполнение накопителя N1:
(S32, S31,...,S2, S1);
32, 31,..., 2, 1 номер разряда N1
исходное заполнение накопителя N2:
(S64, S63,..., S34, S33).
64, 63,..., 34, 33 номер разряда N2
Исходное заполнение N1 и N2 (синхропосылка 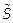 ) зашифровывается в режиме простой замены. Результат зашифрования
) зашифровывается в режиме простой замены. Результат зашифрования
A(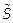 ) = (Y0, Z0)
) = (Y0, Z0)
переписывается в 32-разрядные накопители N3 и N4 так, что заполнение N1 переписывается в N3, а заполнение N2 – в N4.
Заполнение накопителя N4 суммируют по модулю (232 –1) в сумматоре СМ4 с 32-разрядной константой С1 из накопителя N6. Результат записывается в N4. Заполнение накопителя N3 суммируется по модулю 232 в сумматоре СМ3 с 32-разрядной константой С2 из накопителя N5. Результат записывается в N3. Заполнение N3 переписывают в N1, а заполнение N4 – в N2, при этом заполнения N3, N4 сохраняются. Заполнение накопителей N1 и N2 зашифровывается в режиме простой замены.
Полученное в результате зашифрования заполнение накопителей N1, N2 образует первый 64-разрядный блок гаммы шифра Гш(1)=(g1(1), g2(1),..., g63(1), g64(1)), который суммируют поразрядно по модулю 2 в сумматоре СМ5 с первым 64-разрядным блоком открытых данных
Т0(1) = (t1(1), t2(1),..., t63(1), t64(1)).
В результате суммирования по модулю 2 значений Гш(1) и Т0(1) получают первый 64-разрядный блок зашифрованнных данных:
Тш(1) = Гш(1) Å Т0(1) = (t1(1), t2(1),..., t63(1), t64(1)),
где ti(1) = ti(1) Å gi(1), i  {1,…,64}.
{1,…,64}.
Для получения следующего 64-разрядного блока гаммы шифра Гш(2) заполнение N4 суммируется по модулю (232 –1) в сумматоре СМ4 с константой С1 из N6. Результат записывается в N4. Заполнение N3 суммируется по модулю 232 в сумматоре СМ3 с константой С2 из N5. Результат записывается в N3. Новое заполнение N3 переписывают в N1, а новое заполнение N4 – в N2 , при этом заполнения N3 и N4 сохраняют. Заполнения N1, N2 зашифровывают в режиме простой замены.
Полученное в результате зашифрования заполнение накопителей N1 и N2 образует второй 64-разрядный блок гаммы шифра Гш(2), который суммируется поразрядно по модулю 2 в сумматоре СМ5 со вторым блоком открытых данных Т0(2):
Тш(2) = Гш(2) Å Т0(2).
Аналогично вырабатываются блоки гаммы шифра Гш(3), Гш(4),..., Гш(m) и зашифровываются блоки открытых данных Т0(3), Т0(4),..., Т0(m).
В канал связи или память ЭВМ передаются синхропосылка 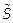 и блоки зашифрованных данных Тш(1), Тш(2),..., Тш(m).
и блоки зашифрованных данных Тш(1), Тш(2),..., Тш(m).
|
|
|
Расшифрование в режиме гаммирования. При расшифровании криптосхема имеет тот же вид, что и при зашифровании (см. рис. 25).
Уравнение расшифрования:
Т0(i) = Тш(i) Å Гш(i) = Tш(i) Å A (Yi–1 ⊞ C2, Zi–1 ⊞´ C1), i  {1,…,m}.
{1,…,m}.
Следует отметить, что расшифрование данных возможно только при наличии синхропосылки, которая не является секретным элементом шифра и может храниться в памяти ЭВМ или передаваться по каналам связи вместе с зашифрованными данными.
Рассмотрим реализацию процедуры расшифрования. В КЗУ вводят 256 бит ключа, с помощью которого осуществляется зашифрование данных Т0(1), Т0(2),..., Т0(m). В накопители N1 и N2 вводится синхропосылка, и осуществляется процесс выработки m блоков гаммы шифра Гш(1), Гш(2),..., Гш(m). Блоки зашифрованных данных Тш(1), Тш(2),..., Тш(m) суммируются поразрядно по модулю 2 в сумматоре СМ5 с блоками гаммы шифра Гш(1),..., Гш(m). В результате получаются блоки открытых данных
Т0(1), Т0(2),..., Т0(m);
при этом Т0(m) может содержать меньше 64 разрядов.
|
|
|


