 |
Электронная цифровая подпись (ЭЦП)
|
|
|
|
5.5.1 Процедуры постановки и проверки ЭЦП
При обмене электронными документами в телекоммуникационных сетях существенно снижаются затраты на обработку и хранение документов, ускоряется их поиск. Но при этом возникает проблема аутентификации автора документа и самого документа, то есть установление подлинности автора и отсутствия изменений в полученном документе.
При обработке документов в электронной форме совершенно непригодны традиционные способы установления подлинности по рукописной подписи и оттиску печати на бумажном документе. Принципиально новым решением является электронная цифровая подпись (ЭЦП).
ЭЦП используется для аутентификации текстов, передаваемых по телекоммуникационным каналам. Функционально она аналогична обычной рукописной подписи и обладает основными ее достоинствами:
- удостоверяет, что подписанный текст исходит от лица, поставившего подпись;
- не дает самому этому лицу возможность отказаться от обязательств, связанных с подписанным текстом;
- гарантирует целостность подписанного текста.
ЭЦП представляет собой относительно небольшое количество дополнительной цифровой информации, передаваемой вместе с подписываемым текстом, и включает две процедуры:
· процедуру постановки подписи, в которой используется секретный ключ отправителя сообщения;
· процедуру проверки подписи, в которой используется открытый ключ отправителя.
Процедура постановки подписи
При формировании ЭЦП, отправитель, прежде всего, вычисляет хэш-функцию m=h(M) подписываемого текста М. Вычисленное значения хэш-функции h(M) представляет собой один короткий блок информации m, характеризующий весь текст М в целом. Затем значение m шифруется секретным ключом отправителя. Получаемая при этом пара чисел представляет собой ЭЦП для данного текста М.
|
|
|
Процедура проверки подписи
При проверке ЭЦП получатель сообщения снова вычисляет хэш-функцию m = h(M) принятого по каналу текста М, после чего при помощи открытого ключа отправителя проверяет, соответствует ли полученная подпись вычисленному значению m хэш-функции.
Принципиальным моментом в системе ЭЦП является невозможность подделки ЭЦП пользователя без знания его секретного ключа.
Каждая подпись, как правило, содержит следующую информацию:
- дату подписи;
- срок окончания действия ключа данной подписи;
- информацию о лице, подписавшем текст;
- идентификатор подписавшего (имя открытого ключа);
- собственно цифровую подпись.
Хэш-функции
Пусть  множество всевозможных сообщений. Множество
множество всевозможных сообщений. Множество  является, вообще говоря, бесконечным. Хэш-функцией называется отображение
является, вообще говоря, бесконечным. Хэш-функцией называется отображение
 ,
,
где М некоторое множествою.
Хэш-функция должна удовлетворять нескольким требованиям, что и позволяет ее использовать в криптографии, в частности, для подписи сообщений.
1) для данного  легко вычислить
легко вычислить 
2) для данного  трудно вычислить
трудно вычислить  такое, что
такое, что 
3) для данного  трудно вычислить
трудно вычислить  ,
,  , такое, что
, такое, что  .
.
Отображение  , удовлетворяющее требованиям 1) и 2), является однонаправленным. Иногда вместо 3) требуют выполнения более сильного свойства.
, удовлетворяющее требованиям 1) и 2), является однонаправленным. Иногда вместо 3) требуют выполнения более сильного свойства.
 трудно вычислить пару
трудно вычислить пару  , для которой
, для которой  .
.
Пара элементов множества  (пара сообщений), о которой идет речь в
(пара сообщений), о которой идет речь в  называется коллизией для отображения
называется коллизией для отображения  . Т.к. мощность
. Т.к. мощность  больше мощности
больше мощности 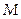 , то
, то  допускает коллизии.
допускает коллизии.
Очевидно, что определение однонаправленной хэш-функции и коллизии не зависит от того, является ли множество  конечным или бесконечным. Несложно показывается, что свойство
конечным или бесконечным. Несложно показывается, что свойство  влечет свойство 3). Оказывается, что при выполнении нескольких естественных предположений условие
влечет свойство 3). Оказывается, что при выполнении нескольких естественных предположений условие  влечет выполнение условия 2).
влечет выполнение условия 2).
|
|
|
Как правило, в качестве  берут множество I
берут множество I  всех слов конечной длины в некотором алфавите I = {i
всех слов конечной длины в некотором алфавите I = {i  ,...,i
,...,i  }, а в качестве
}, а в качестве 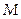 множество I
множество I  всех слов длины L алфавита. На практике, чаще всего I=F2, I
всех слов длины L алфавита. На практике, чаще всего I=F2, I  =
=  – множество слов конечной длины в двоичном алфавите F2={0,1}. От функции H: I
– множество слов конечной длины в двоичном алфавите F2={0,1}. От функции H: I  ®IL, требуют, чтобы она обладала свойством: значения H на словах, которые даже имеют отличие друг от друга только в одном знаке, дают значительно отличающиеся хэш-значения. Тогда, получив на приемном конце сообщение и его хэш (
®IL, требуют, чтобы она обладала свойством: значения H на словах, которые даже имеют отличие друг от друга только в одном знаке, дают значительно отличающиеся хэш-значения. Тогда, получив на приемном конце сообщение и его хэш ( ), можно вычислить значение хэш от сообщения, сравнить с полученным хэш по каналу связи, и подтвердить или опровергнуть, что сообщение не искажено.
), можно вычислить значение хэш от сообщения, сравнить с полученным хэш по каналу связи, и подтвердить или опровергнуть, что сообщение не искажено.
Если функция H зависит также от ключа kÎK, то помимо проверки целостности добавление значения хэш к сообщению подтверждает истинность сообщения. Такой способ подтверждения истинности называется кодом аутентификации (Message Autentification Code – MAC). Однако, такое подтверждение истинности еще не является электронной подписью. Подтверждение истины называется подписью, если ее могут проверить все, не знающие ключи. Например, в суде можно поверить истинность, не раскрывая ключи. Приведенный выше способ проверки подлинности сообщения непригоден, так как влечет раскрытие ключа. Для того, чтобы код аутентификации стал электронной подписью сообщения, необходимо использовать хэш-функции с дополнительными свойствами. Например, использовать систему с открытым ключом. Напомним вкратце суть электронной подписи. Пусть у корреспондента В имеются два алгоритма Е  и D
и D  , каждый из которых преобразует слово из
, каждый из которых преобразует слово из 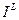 в слово из
в слово из 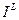 и каждый определен на
и каждый определен на 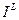 . Первый алгоритм известен всем, а второй – только владельцу В. Обладание алгоритмом D
. Первый алгоритм известен всем, а второй – только владельцу В. Обладание алгоритмом D  однозначно (юридически) определяет корреспондента В. Считаем, что Е
однозначно (юридически) определяет корреспондента В. Считаем, что Е  и D
и D  удовлетворяют соотношениям для любого a Î
удовлетворяют соотношениям для любого a Î 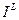
Е  D
D  (a) = a, D
(a) = a, D  Е
Е  (a) = a.
(a) = a.
Тогда электронной подписью документа МÎ А  называется
называется
С = D  (h(М)).
(h(М)).
Проверка подписи под документом М возможна любым лицом, у которого есть Е  . Для этого проверяющий вычисляет H (М) (Н() – известна всем, М проверяющий получает вместе с подписью С). Второй шаг проверки – вычисление
. Для этого проверяющий вычисляет H (М) (Н() – известна всем, М проверяющий получает вместе с подписью С). Второй шаг проверки – вычисление
Е  (С) = Е
(С) = Е  D
D  (H(М)) = H(М).
(H(М)) = H(М).
Если вычисленное значение хэш от Мсовпало с результатом применения алгоритмов Е  к С, то подпись В считается подтвержденной (даже в суде).
к С, то подпись В считается подтвержденной (даже в суде).
|
|
|
Пример. Обычно хэш h() строится следующим образом. Выбирается функция h:  ´
´  ®
®  , удовлетворяющая свойствам 1-3. Например, когда длина L хэш была 64 бита, то брали следующую схему
, удовлетворяющая свойствам 1-3. Например, когда длина L хэш была 64 бита, то брали следующую схему
 х k
х k
DES
ключ
Z
z = h(x,k) = DES  (x).
(x).
2) " a Î А  , a = a
, a = a  ...a
...a  ,
,
где длина блока a  равна L, а блок a
равна L, а блок a  дополнен до блока длины L (если это необходимо). Н(a) вычисляется по следующему алгоритму.
дополнен до блока длины L (если это необходимо). Н(a) вычисляется по следующему алгоритму.
b  = h(a
= h(a  ,a
,a  )
)
b  =h(b
=h(b  ,a
,a  )
)
………………..
b  =h(b
=h(b 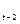 ,a
,a  ).
).
Известно следующее
УТВЕРЖДЕНИЕ. Пусть  – конечные множества, и
– конечные множества, и  . Задано произвольное отображение
. Задано произвольное отображение  . Пусть для любого
. Пусть для любого  имеется эффективный алгоритм вычисления
имеется эффективный алгоритм вычисления 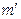 такого, что
такого, что  (если
(если 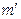 существует), при этом алгоритм задает равномерное распределение на множестве таких
существует), при этом алгоритм задает равномерное распределение на множестве таких 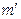 при всех
при всех  . Тогда имеется эффективный алгоритм вычисления коллизии для функции H.
. Тогда имеется эффективный алгоритм вычисления коллизии для функции H.
ДОКАЗАТЕЛЬСТВО. Обозначим через  алгоритм обращения
алгоритм обращения  , о котором идет речь в формулировке леммы. То есть
, о котором идет речь в формулировке леммы. То есть  для некоторого
для некоторого 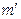 такого, что
такого, что  . Сформулируем алгоритм вычисления коллизии.
. Сформулируем алгоритм вычисления коллизии.
Входные данные алгоритма: хэш-функция  , алгоритм
, алгоритм  . Выходные данные алгоритма: коллизия для H.
. Выходные данные алгоритма: коллизия для H.
Шаг 1. Выбрать случайное  , вычислить
, вычислить  .
.
Шаг 2. Вычислить 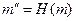 .
.
Шаг 3. Если  , то перейти к шагу 1; в противном случае
, то перейти к шагу 1; в противном случае  – коллизия для H. Алгоритм заканчивает работу.
– коллизия для H. Алгоритм заканчивает работу.
Оценим среднее число прохождений алгоритма через шаг 1. Имеем вероятностную схему, исходами которой являются пары  , где
, где  . Обозначим через
. Обозначим через  множество
множество  , для которых
, для которых  . Заметим, что число классов
. Заметим, что число классов  не больше
не больше  . Тогда вероятность исхода
. Тогда вероятность исхода  равна
равна  . Благоприятными являются исходы
. Благоприятными являются исходы  , где
, где  . Найдем вероятность неблагоприятного исхода. Она равна
. Найдем вероятность неблагоприятного исхода. Она равна
 .
.
Отсюда вероятность благоприятного исхода не меньше  . Следовательно, среднее число прохождений алгоритма через шаг 1 не превосходит 2, то есть этот алгоритм эффективен.
. Следовательно, среднее число прохождений алгоритма через шаг 1 не превосходит 2, то есть этот алгоритм эффективен.
|
|
|


