Алгоритм цифровой подписи DSA

Американский стандарт цифровой подписи состоит из трех частей: алгоритма хэширования SHA (Secure Hash Algorithm), алгоритм порождения параметров p, q и алгоритм подписи DSA (Digital Signature Algorithm). Алгоритм цифровой подписи DSA (Digital Signature Algorithm) используется в стандарте цифровой подписи DSS (Digital Signature Standard).

Отправитель и получатель электронного документа используют при вычислении большие простые числа: g и p по L бит каждое (512 £ L £ 1024); q – простой делитель числа (p –1), число q имеет длину 160 бит (делитель). Числа g, p, q являются открытыми и могут быть общими для всех пользователей сети.

Отправитель выбирает случайное целое число x, 1< x< q. Число x является секретным ключом отправителя для формирования электронной цифровой подписи.

Затем отправитель вычисляет значение

y = g^x mod p.

Число y является открытым ключом для проверки подписи отправителя. Число y передается всем получателям документов.

Этот алгоритм также предусматривает использование односторонней функции хэширования h(·). В стандарте DSS определен так называемый алгоритм безопасного хэширования SHA (Secure Hash Algorithm).

Для того чтобы подписать документ M, отправитель хэширует его в целое хэш-значение m:

m = H(M), 1< m < q,

затем генерирует случайное целое число k, 1< k< q, и вычисляет число r:

r = (g^k mod p) mod q.

Затем отправитель вычисляет с помощью секретного ключа x целое число s:

s = mod q.

Пара чисел r и s образует цифровую подпись (r,s)

под документом M.

Таким образом, подписанное сообщение представляет собой тройку чисел [M, r, s].

Получатель подписанного сообщения [M, r, s] проверяет выполнение условий

0 < r < q,

0 < s < q

и отвергает подпись, если хотя бы одно из этих условий не выполнено.

Затем получатель вычисляет значение

w = mod q,

и хэш-значение

m = H(M),

а затем числа

u₁ = (m∙ w) mod q,

u₂ = (r∙ w) mod q.

Далее получатель с помощью открытого ключа y вычисляет значение

v = ((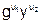) mod p) mod q

и проверяет выполнение условия

v = r.

Если условие v = r выполняется, тогда подпись (r,s) под документом M признается получателем подлинной.

Доказано, что последнее равенство будет выполняться тогда, и только тогда, когда подпись (r,s) под документом M получена с помощью именно с того секретного ключа x, из которого был получен открытый ключ y. Таким образом, можно надежно удостовериться, что отправитель сообщения владеет именно данным секретным ключом x
(не раскрывая при этом значения ключа x) и что данный документ M подписал именно отправитель

По сравнению с алгоритмом цифровой подписи Эль–Гамаля алгоритм DSA имеет следующие основные преимущества:

1. При любом допустимом уровне стойкости, т.е. при любой паре чисел g и p (от 512 до 1024 бит),

числа q, x, r, s имеют длину по 160 бит, сокращая длину подписи до 320 бит.

2. Большинство операций с числами k, r, s, x при вычислении подписи производится по модулю числа q длиной 160 бит, что сокращает время вычисления подписи.

3. При проверке подписи большинство операций с числами u₁, u₂, v, w также производится по модулю числа q длиной 160 бит, что сокращает объем памяти и время вычисления.

Недостатком алгоритма DSA является то, что при подписывании и при проверке подписи приходится выполнять сложные операции деления по модулю q:

s = (mod q), w = 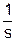(mod q),

что не позволяет получать максимальное быстродействие.

Следует отметить, что реальное исполнение алгоритма DSA может быть ускорено с помощью выполнения предварительных вычислений. Заметим, что значение r не зависит от сообщения M и его хэш-значения m. Можно заранее создать строку случайных значений k и затем для каждого из этих значений вычислить значения r. Можно также заранее вычислить обратные значения k^–1 для каждого из значений k. Затем, при поступлении сообщения M, можно вычислить значение s для данных значений r и k^–1. Эти предварительные вычисления значительно ускоряют работу алгоритма DSA.

Стойкость алгоритма подписи DSA определяется сложностью решения задачи дискретного логарифмирования в подгруппе порядка q. Для ее решения можно применить два подхода.

Во-первых, можно вычислить дискретные логарифмы y, g по основанию R, где 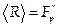, использовав какой-либо современный вариант индекс – метода (смотри раздел, посвященный дискретным логарифмам). Например, метод решета числового поля или линейное решето. Отсюда легко найти логарифм y по основанию q, то есть секретный ключ x.

Во-вторых, можно использовать r-метод Полларда и его распараллеливание
(см. тот же раздел) для прямого вычисления x. При выборе величины q надо учитывать оба подхода.

При анализе алгоритма подписи Эль–Гамаля мы видели, что централизованное порождение параметров может быть опасно. Это было учтено при разработке стандарта США. Помимо простых чисел p и q пользователю предоставляют значения S, C параметров алгоритма выработки этих p и q. Зная S, C, пользователь может проверить действительно ли числа p,q были получены с помощью этого алгоритма. Приведем теперь сам алгоритм.

Входные данные алгоритма. Число L, где 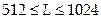и 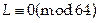. Пусть 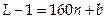, где 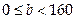. Выходные данные алгоритма. Простое число p длины L бит, простое число q длины 160 бит, двоичная последовательность S и число C, .

Шаг 1. Выбрать произвольную последовательность бит S, длина g которой не менее 160.

Шаг 2. Вычислить . Таким образом, U – вектор длины 160. Здесь SHA(S) есть результат применения алгоритма SHA.

Шаг 3. Образовать q, установив первый и 160-й бит U в 1. Таким образом, q – нечетное число длиной 160 бит.

Шаг 4. Проверить q на простоту.

Шаг 5. Если q составное, то перейти на шаг 1. Если q простое, то перейти на шаг 6.

Шаг 6. Положить C=0, N=2.

Шаг 7. Вычислить 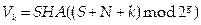при всех k, .

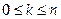Шаг 8. Пусть W целое число

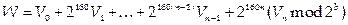
длины не более L-1 бит. Положить 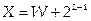. Таким образом, X – число, длина которого в точности равна L бит.

Шаг 9. Положить 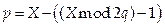. Тогда .

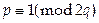Шаг 10. Если , то перейти к шагу 13.

Шаг 11. Проверить p на простоту.

Шаг 12. Если p простое, то перейти к шагу 15. В противном случае, перейти на шаг 13.

Шаг 13. Положить C:=C+1 и N:=N+n+1.

Шаг 14. Если C=4096, то перейти на шаг 1. В противном случае перейти к шагу 7.

Шаг 15. Сохранить числа p, q, C и последовательность S. Закончить алгоритм.

Заметим, что для проверки простоты чисел p, q рекомендуется использовать вероятностный тест, то есть тест типа Монте–Карло с вероятностью ошибки не более 2^-80.

⇐ Предыдущая18192021222324252627Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: