Алгоритм неоспоримой цифровой подписи Д.Чома

Рассмотрим алгоритм неоспоримой цифровой подписи, разработанный Д.Чомом. Сначала опишем алгоритм генерации ключей, с помощью которого каждая сторона А, подписывающая документ, выбирает секретный ключ и соответствующий открытый ключ.

Каждая сторона А должна выполнить следующее:

1. Выбрать случайное простое число p = 2q + 1, где q – также простое число.

2. Выбрать генераторное число a для подгруппы порядка q в циклической группе Z_p^*:

2.1. Выбрать случайный элемент b Î Z_p^* и вычислить a = b^(p-1)/q mod p.

2.2. Если a = 1, тогда возвратиться к шагу 2.1.

3. Выбрать случайное целое x Î{1, 2,..., q-1} и вычислить у = a^x mod p.

4. Для стороны А открытый ключ равен (p, a, y), секретный ключ равен x.

Согласно алгоритму неоспоримой подписи Д.Чома, сторона А подписывает сообщение m, принадлежащее подгруппе порядка q в Z_p^*. Любая сторона В может проверить эту подпись при участии А.

В работе алгоритма неоспоримой подписи можно выделить два этапа:

1. Генерация подписи,

2. Верификация подписи.

На этапе генерации подписи сторона А вычисляет

s = m^x mod p,

где s – подпись стороны А на сообщении m.

 

Сообщение m с подписью s отсылается стороне В.

Этап верификации подписи выполняется стороной В с участием стороны А и включает следующие шаги:

(1) В получает подлинный открытый ключ (p, a, y) стороны А.

(2) В выбирает два случайных секретных целых числа a, b Î {1, 2,..., q-1}.

(3) B вычисляет z = s^a y^b mod p и отправляет значение z стороне А.

(4) А вычисляет w = (z)^1/x mod p, где хх^-1 º 1 (mod q), и отправляет значение w стороне В.

(5) В вычисляет w’ = m^a a^b mod p и признает подпись s подлинной, если и только если w = w’.

Убедимся, что проверка подписи s работает:

w º (z)^1/x º (s^a y^b)^1/x º (m^xaa^xb)^1/x º m^aa^b º w’mod p.

Можно показать, что с высокой степенью вероятности злоумышленник не сможет заставить В принять фальшивую подпись. Предположим, что s представляет собой подделку подписи стороны А на сообщении m, т.е. s ¹ m^x mod p. Тогда вероятность принятия стороной этой подписи в данном алгоритме составляет только 1/q, причем эта вероятность не зависит от вычислительных ресурсов злоумышленника.

Подписавшая сторона А при некоторых обстоятельствах могла бы попытаться отказаться от своей подлинной подписи одним из трех способов:

(а) отказаться от участия в протоколе верификации;

(б) некорректно выполнить протокол верификации;

(в) объявить подпись фальшивой, даже если протокол верификации оказался успешным.

Отречение от подписи способом (а) рассматривалось бы как очевидная попытка неправомерного отказа.

Против способов (б) и (в) бороться труднее, здесь требуется специальный протокол дезавуирования. Этот протокол определяет, пытается ли подписавшая сторона А дезавуировать правильную подпись s или эта подпись является фальшивой. В этом протоколе по существу дважды применяется протокол верификации и затем производится проверка с целью убедиться, что сторона А выполняет этот протокол корректно.

Протокол дезавуирования для схемы неоспоримой подписи Д.Чома включает следующие шаги:

(1) В принимает от стороны А сообщение m с подписью s и получает подлинный открытый ключ (p, a, y) стороны А.

(2) В выбирает случайные секретные целые числа a, bÎ{1,2,...,q-1}, вычисляет z = s^a y^b mod p и отправляет значение z стороне А.

(3) А вычисляет w = (z)^1/x mod p, где xx^-1 º 1(modq), и отправляет значение w стороне В.

(4) Если w = m^a a^b modp, тогда В признает подпись s подлинной и протокол прекращается.

(5) В выбирает случайные секретные целые числа a’, b’ Î {1, 2,..., q-1}, вычисляет z’= s^a’y^b’mod p и отправляет значение z’ стороне А.

(6) А вычисляет w’= (z’)^1/x modp и отправляет значение w’ стороне В.

(7) Если w’ = m^a’a^b’ modp, тогда В принимает подпись s и протокол останавливается.

(8) В вычисляет c = (wa^-b)^a’ mod p, c’= (w’a^-b’)^a mod p. Если с = c’, тогда В заключает, что подпись s фальшивая; в противном случае, В делает вывод, что подпись s подлинная, а сторона А пытается дезавуировать подпись s.

Нетрудно убедиться в том, что этот протокол достигает поставленной цели. Пусть m – сообщение и предположим, что s – подпись стороны А под сообщением m.

Если подпись s фальшивая, т.е. s ¹ m^x modp и если стороны А и В следуют протоколу должным образом, тогда w = w’ (и поэтому справедливо заключение В, что подпись s фальшивая).

Пусть s на самом деле является подписью стороны А под сообщением m, т.е. s = m^x mod p. Предположим, что В точно следует протоколу, а А не следует. Тогда вероятность того, что w=w’ (и А преуспевает в дезавуировании подписи), составляет только 1/q.

Следует отметить, что третья сторона С никогда не должна принимать в качестве доказательства подлинности подписи s запись стороной В протокола верификации, поскольку сторона В может выдумать успешную запись шага 2 и последующих шагов протокола верификации без участия подписывающей стороны А.

Неоспоримая подпись может быть верифицирована только путем непосредственного взаимодействия с подписывающей стороной А. Разработан также алгоритм для обратимой неоспоримой подписи, которая может быть верифицирована, дезавуирована, а также преобразована в обычную цифровую подпись. Этот алгоритм основан на использовании алгоритма цифровой подписи Эль-Гамаля.

Протокол подписи, позволяющий отправителю сообщения не предоставлять право
получателю доказывать справедливость своей подписи

Цифровая подпись может обладать свойствами, которые не присущи обычной подписи. Пусть отправитель сообщения А производит некий программный продукт и поставляет его на рынок. Чтобы обезопасить свои программы от подделок, А подписывает их с помощью своего секретного алгоритма. Покупатель Б проверяет подпись А и тем самым убеждается, что он не обманут. В то же время пираты заинтересованы в продаже копий программ А, по той же высокой цене. Они хотят доказать покупателю, что эти продукты производятся именно А. Имеется протокол подписи, разработанный Шаумом, который позволяет А предоставлять или не предоставлять покупателю Б право проверки своей подписи.

Зафиксируем конечное поле 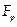, где p – простое число.

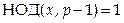Пусть g – первообразный вычет по mod p. Вычет , где , есть секретный ключ А.

Пусть сообщение (хэш-значение сообщения). Отправитель сообщения А вычисляет подпись под сообщением m. Таки образом (m,c) есть подписанный документ.

Протокол проверки подписи:

Получатель Б выбирает случайный вычет , вычисляет и передает вычет z отправителю А,

Отправитель А вычисляет и и передает d получателю Б,

Получатель Б проверяет сравнение 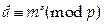. Если оно выполнено, то Б принимает подпись, в противном случае подпись отвергается.

Легко проверить, если подпись верна, то выполняется сравнение 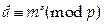. Пусть теперь Б хочет продать копию документа m другому персонажу К. Б должен убедить К, что именно А подписал m. Для этого Б показывает запись протокола проверки подписи. Однако, К мог бы составить такую запись сам, не общаясь с А. Действительно, надо сгенерировать случайное и и вычислить 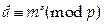. Таким образом, Б не в состоянии доказать, что именно А подписал сообщение m.

Очевидно, что приведенный протокол является протоколом с нулевым раскрытием. Таким образом, запись протокола не предоставляет противнику никакой новой информации о секретном ключе А помимо той, которая содержится в сравнении .

 

⇐ Предыдущая19202122232425262728Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: