Схемы предварительного распределения ключей в сети связи

Если число абонентов сети засекреченной связи невелико, то и число распределяемых ключей также невелико. Для больших же сетей распределение ключей становится очень серьезной проблемой. Она заключается в том, что для сети, в которой работают п абонентов, необходимо выработать заранее и хранить в дальнейшем п (п- 1) / 2ключей. Кроме того, каждому абоненту сети необходимо передать ключи для связи с остальными n - 1 абонентами, которые абонент должен постоянно хранить. Например, для сети со 100 абонентами нужно сгенерировать и хранить почти 5000 ключей, причем каждый абонент при этом должен хранить у себя 99 ключей.

Для уменьшения объема хранимой ключевой информации применяются различные схемы предварительного распределения ключей в сети связи. Их суть заключается в том, что в действительности вначале происходит распределение не самих ключей, а некоторых вспомогательных ключевых материалов, занимающих меньшие объемы. На основании этих материалов каждый абонент сети может самостоятельно вычислить по некоторому алгоритму необходимый для связи ключ. Такой подход позволяет уменьшить объемы как хранимой, так и распределяемой секретной информации.

В качестве примера рассмотрим схему Блома распределения ключей между п абонентами, для которой процедура вычисления ключа заключается в вычислении значения некоторого симметрического многочлена над конечным полем.

Выберем поле F, имеющее конечное, но достаточно большое число элементов, и зафиксируем п различных элементов r ₁ ,..., r_n Î F, отличных от нуля. Каждый элемент r_i

припишем i -му абоненту сети, i = . Эти элементы не являются секретными и могут храниться на общедоступном сервере сети. Выберем теперь многочлен над полем F степени 2т, 1 ≤ т < п, вида

где а_ij = a_ji, i ≠ j, i,j = 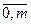. Его коэффициенты являются секретными и должны храниться только в центре распределения ключей. Каждый абонент А получает в качестве ключевых

материалов набор , состоящий из коэффициентов многочлена

Для связи между абонентами А и В теперь можно использовать общий ключ k_AB:

k_AB = k_ВА = f (r_A,r_B)= g_B (r_A) = g_A (r_B),

вычисляемый по формуле:

в матричном виде:

где матрица составлена из коэффициентов многочлена f (x, y) и является симметричной.

При использовании данной схемы каждый абонент должен хранить т+ 1секретных значений вместо п - 1, общее же число секретных коэффициентов многочлена f равно т (т+ 1) / 2.

Для заданного числа т схема Блома дает минимальное по объему количество хранимых у абонента ключевых материалов.

Схема предварительного распределения ключей KDP (key distribution patterns)основана на схеме пересечений множеств.

Пусть имеется п, п > 2, абонентов (пользователей) и множество секретных ключей К, | К | = q. Будем считать, что все ключи перенумерованы числами 1,2,..., q. Выберем некоторое семейство { S ₁ ,...,S_n }подмножеств множества {1,2,..., q }. Предварительно абоненту i по защищенному каналу передается множество секретных ключей с номерами из подмножества S_i, . Таким образом, семейство { S ₁ ,...,S_n }представляет собой таблицу с номерами ключей каждого пользователя. Хотя данная таблица является несекретной, она должна быть защищена от модификаций и подделок.

Если абонент i хочет связаться с абонентом j, то он использует для выработки общего ключа множество ключей, номера которых содержатся в пересечении S_i Ç S_j. Если каждый ключ представлен некоторой битовой строкой, то для формирования общего связного ключа можно взять, например, их сумму, или значение некоторой хэш-функции от строки, составленной из ключей, номера которых входят в пересечение множеств S_i Ç S_j.

Схемой распределения ключей типа KDP, или KDP(n,q)-схемой, назовем всякое семейство { S ₁ ,...,S_n }подмножеств множества К, удовлетворяющее следующему условию:

если при некоторых i,j, r Î{1 ≤ i < j ≤ n} выполнено включение S_i Ç S_j Í S_r, то либо i = r, либо j= r.

Это условие означает, что общий ключ двух абонентов не должен быть известным никакому другому абоненту.

Семейство подмножеств называется семейством Шпернера, если ни одно из них не содержится в другом.

Семейство{ S ₁ ,...,S_n }подмножеств множества К, | К | = q, образует KDP (n,q) - cxeмy втом и только в том случае, если множество{ S_i Ç S_j | 1 ≤ i < j ≤ n } образует семействоШпернера.

Если подмножества{ S ₁ ,...,S_m }множества К, | К | = q, образуют семейство Шпернера, то

Равенство достигается только в случае, если множество{ S ₁ ,...,S_m } совпадает с множеством всех w-элементных подмножеств множества К, где w = q/ 2при четном q и w = (q+ 1) / 2или(q- l)/2 при нечетном q.

Для любой KDP(n,q)- cxeмы каждый абонент должен иметь не менееlog₂ п ключей. Если п ³ 4, то q ³2log₂ n.

Схемы разделения секрета

Схема разделения секрета представляет собой схему предварительного распределения ключей между уполномоченными группами пользователей, в которой ключ заранее определен и одинаков для каждой уполномоченной группы. При этом каждый пользователь получает свою долю или "часть секрета". Схема включает два протокола: протокол формирования долей (разделения секрета) и распределения их между пользователями и протокол восстановления секрета группой пользователей. Схема должна позволять восстанавливать ключ только тем группам пользователей, которые имеют на это полномочия, и никакая другая группа не должна иметь возможности для восстановления ключа или получения о нем какой-либо информации.

Основное назначение схемы разделения секрета — защита ключа от потери. Обычно для защиты от потери делают несколько копий ключа. С возрастанием числа копий ключа возрастает вероятность его компрометации. Если число копий мало, то велик риск потери ключа. Поэтому лучше "разделить" ключ между несколькими лицами так, чтобы допускалась возможность восстановления ключа при различных обстоятельствах несколькими уполномоченными группами с заранее оговоренным составом участников. Тем самым исключается риск безвозвратной потери ключа.

Еще одно положительное качество схем разделения секрета заключается в разделении ответственности за принятие решения, которое автоматически вводится при определении состава уполномоченных групп. Такая коллективная ответственность нужна для многих приложений, включая принятие важных решений, касающихся применения систем оружия, подписания корпоративных чеков или допуска к банковскому хранилищу.

В простейшем случае, когда имеется только одна группа, состоящая из t пользователей, уполномоченная формировать ключ, схему разделения секрета можно построить следующим образом. Предположим, к примеру, что ключ представляет собой двоичный вектор s длины т. Выберем случайным образом t векторов s ₁ ,...,s_t так, чтобы их сумма совпадала с вектором s, и распределим их между пользователями. Теперь, собравшись вместе, они могут легко восстановить значение ключа s, в то время как никакая группа, состоящая из меньшего числа пользователей, не сможет этого сделать. Действительно, в данном случае отсутствие хотя бы одной доли приводит к полной неопределенности относительно значения секрета, поскольку для каждого значения искомого секрета найдется возможный вариант значения отсутствующей доли.

Заметим, что если бы мы в предыдущем примере просто разбили вектор на t частей, то такая схема не могла быть схемой разделения секрета, так как знание любой доли давало бы частичную информацию о секрете s.

Другой пример схемы разделения секрета дает пороговая схема Шамира. Пусть 1 < t ≤ п. Схема разделения секрета между п пользователями называется (n,t) -пороговой, если любая группа из t пользователей может восстановить секрет, в то время как никакая группа из меньшего числа пользователей не может получить никакой информации о секрете.

Для построения (n,t)-пороговой схемы А. Шамир предложил использовать многочлен степени t – 1над конечным полем с достаточно большим числом элементов. Многочлен степени t - 1 можно однозначно восстановить по его значениям в t различных точках, но при этом меньшее число точек использовать для интерполяции нельзя.

Выберем поле F и зафиксируем п различных несекретных элементов r ₁,..., r_n Î F, отличных от нуля. Каждый элемент r_i, приписан i -му абоненту сети, . Выберем также t случайных элементов а ₀,..., а_{i -1} поля F и составим из них многочлен f (х) над полем F степени t - 1, 1 < t ≤ n,

Положим s = f (0) = а ₀. Вычислим теперь значения

s ₁ = f (r ₁),…, s_n = f (r_n)

и распределим в качестве долей между участниками наборы

Для восстановления секрета S можно воспользоваться интерполяционной формулой Лагранжа. Путь имеются t пар (х_i, у_i), где y_i = f (x_i). Тогда формула Лагранжа имеет вид

Так как s = f (0), то из формулы Лагранжа получаем равенства

причем коэффициенты с, не зависят от коэффициентов многочлена f (x) и могут быть вычислены заранее.

С помощью полученной формулы любая группа из t пользователей может легко восстановить секрет. В то же время можно показать, что никакая группа из меньшего числа пользователей не может получить никакой информации о секрете (докажите это самостоятельно).

Схема Шамира удобна тем, что она позволяет легко увеличивать число пользователей. Для этого не нужно ничего менять, кроме множества { r ₁ ,..., r_п }, к которому следует добавить новые элементы r_{n+ 1},..., r_{n+ w}. Компрометация одной доли делает из (n,t)-пороговой схемы (п -1, t -1)-пороговую схему.

⇐ Предыдущая13141516171819202122Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: