Дифференциальный криптоанализ.

Первые открытые упоминания в литературе с 1990 года в работах Мерфи, Бихема и Шамира. Методика анализа строится индивидуально для каждого алгоритма и основана на знании пар сообщений m и m’ для которых известны соответствующие шифртексты E_k (m) и E_k (m’) и XOR-разности между ними с рассмотрением разности между промежуточными частями блоков сообщений.

Для двухветвевой сети Файстеля Δ m_i = m_i Å m’_i. При этом для каждого раунда в отдельности справедливо следующее:

Δ m_{i+ 1} = m_{i+ 1} Å m’_{i +1} = Δ m_{i- 1} Å [ f (m_i, K_i) Å f (m’_i, K_i)]

Предполагается, что для многих пар входных данных функции f, имеющих одну и ту же XOR-разность, при использовании одного и того же подключа одинаковой оказывается и XOR-разность для соответствующих выходных пар. Формально говорят, что X влечет Y с вероятностью р, если для относительной доли р входных пар с XOR-разностью Х для соответствующих выходных пар XOR-разность оказывается равной Y. Предположим теперь, что имеется ряд значений X, которые с высокой вероятностью влекут определенные разности выходных значений. Тогда если нам с большой вероятностью известны значения Δ m_{i- 1} и Δ m_i то мы с большой вероятностью можем определить и Δ m_i- ₁. А если удастся найти достаточно много таких значений разности, становится возможным определить подключ, используемый функцией f.

Общая стратегия дифференциального криптоанализа основывается на представленной выше методике для каждого раунда шифрования в отдельности. Процедура начинается с рассмотрения двух сообщений открытого текста m и m ' с заданной разностью и имеет своей целью получение вероятностных оценок разностей промежуточных результатов последовательно раунд за раундом с тем, чтобы определить вероятностную оценку для разности соответствующих шифрованных текстов. На самом деле получаются вероятностные оценки для двух 32-битовых половинок сообщения (m ₁₇ || m ₁₆). После этого выполняется шифрование m и m’, чтобы определить реальные разности при неизвестном ключе, а затем, сравнить результат с вычисленными вероятностными оценками. Если результаты совпадают, т.е.

Е_к (m) Å Е_к (m’) = (Δ m ₁₇|| m ₁₆),

то можно ожидать, что вероятностные оценки для всех раундов соответствуют реальности. Это позволяет сделать определенные заключения о некоторых битах ключа. Чтобы определить все биты ключа, процедуру приходится повторять много раз.

Линейный криптоанализ.

Более новым направлением в криптоанализе является линейный криптоанализ. Метод линейного криптоанализа заключается в построении линейной аппроксимации преобразования, выполняемого в ходе шифрования DES. Данный метод позволяет найти ключ DES при наличии 2⁴⁷ известных фрагментов открытого текста, тогда как для дифференциального криптоанализа требуется 2⁴⁷фрагментов избранного открытого текста.

Пусть для шифра с n -битовыми блоками открытого и шифрованного текста и m -битовым ключом блок открытого текста будет обозначен Р[1],...,Р[ n ], блок шифрованного текста - С[1],..., С[ n ], а ключ - К[1],..., K[ n ]. Тогда определим

A[ i,j,…,k ] = A[ i ] Å A[ j ] Å...ÅA[ k ].

Целью линейного криптоанализа является нахождение подходящего линейного уравнения вида

Р[α₁, α₂„..., α_a] Å С[β₁, β₂,..., β_b] = К[γ₁, γ₂,..., γ_c],

выполняющегося с вероятностью р ¹0,5 (где х = 0 или 1, 1 ≤ а, b ≤ n, 1 ≤ с ≤ т, а α, βи γпредставляют фиксированные битовые позиции в блоках). Чем больше значение р отклоняется от 0,5, тем более подходящим считается уравнение. После этого вычисляются значения левой части данного уравнения для большого числа пар соответствующих фрагментов открытого и шифрованного текста. Если результат оказывается равным 0 более чем в половине случаев, полагают, что K[γ₁, γ₂,..., γ_c] = 0. Если же в большинстве случаев получается 1, полагают, что K[γ₁, γ₂,..., γ_c] = 1. Достаточное количество полученных таким образом равенств образуют систему, решением которой определяется ключ. Ввиду линейности получаемых уравнений, проблему можно решать для каждого раунда шифрования в отдельности, а полученные результаты затем объединить.

Атаки на хэш-функции и коды аутентичности.

Атака «дней рождения»

Этот тип атаки, основан на том факте, что одинаковые значения, называемые также коллизиями (collisions), появляются намного быстрее, чем можно было ожидать. В системе финансовых транзакций, в которой для обеспечения безопасности каждой транзакции применяется новый 64-битовый ключ аутентификации. (Для простоты предполагается, что шифрование не используется.) Существует 2⁶⁴ возможных значения ключа (это больше, чем 18·10¹⁸, т.е. 18 миллиардов миллиардов). Отследив около 2³² транзакций, злоумышленник может предположить, что две из них используют один и тот же ключ. Предположим, что сообщение-заголовок, передаваемый в ходе каждой транзакции, всегда одинаково. Если две транзакции используют один и тот же ключ аутентификации, тогда значения MAC первых сообщений этих транзакций будут совпадать, что легко отследит злоумышленник. Зная, что обе транзакции используют один и тот же ключ аутентификации, он сможет вставлять сообщения из более старой транзакции в более новую транзакцию во время выполнения последней. Поскольку ложные сообщения успешно пройдут аутентификацию, они будут приняты, что является очевидным взломом системы финансовых транзакций.

В общем случае, если элемент может принимать N различных значений, ожидать первой коллизии можно после случайного выбора приблизительно 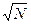элементов. В большинстве случаев мы будем говорят об n -битовых значениях. Поскольку n -битовый элемент может иметь 2 ⁿ возможных значения, необходимо извлечь = 2 ^{n /2} элементов множества, чтобы надеяться на возникновение коллизии. Назовем это оценкой 2 ^{n /2} или оценкой парадокса задачи о днях рождения (birthday bound).

Двусторонняя атака

Является разновидностью атак, в основе которых лежит парадокс задачи о днях рождения, носит также название атаки "встреча на середине" (meet-in-the-middle attacks). (В совокупности оба типа атак называются атаками на основе коллизий (collision attacks).) Этот тип атак более распространен и более результативен.

В системе финансовых транзакций, в которой для каждой транзакции используется новый 64-битовый ключ, используя двустороннюю атаку, злоумышленник может еще более продвинуться во взломе системы. Для этого он случайным образом выбирает 2³² различных 64-битовых ключа. По каждому из них он подсчитывает значение MAC для сообщения-заголовка. Полученное значение MAC вместе с соответствующим ключом помещается в таблицу. Затем злоумышленник прослушивает каждую транзакцию и проверяет, не окажется ли значение MAC первого сообщения этой транзакции в его таблице. Если такая транзакция находится, значит, с высокой долей вероятности ее ключом аутентификации является тот самый ключ, который был сгенерирован злоумышленником и помещен в таблицу вместе с соответствующим значением MAC. Теперь, когда злоумышленник обладает ключом аутентификации транзакции, он может вставлять в нее собственные сообщения с любым нужным ему текстом. (Предыдущий тип атаки позволял злоумышленнику вставлять только сообщения, взятые из более старой транзакции.)

После 2³² транзакций злоумышленник может ожидать появление транзакции, использующей ключ из его таблицы. Таким образом, злоумышленнику придется проделать 2³² предварительных подсчета и прослушать 2³² транзакции. Это намного меньше, чем перебирать все 2⁶⁴ возможных ключа.

Различие между атакой, в основе которой лежит парадокс задачи о днях рождения, и двусторонней атакой состоит в следующем. В первом случае мы ждем, когда одно и то же значение появится дважды в одном множестве элементов. В двусторонней атаке у нас есть два множества элементов, и мы ждем, когда эти множества пересекутся. И в том и в другом случае ожидать первого результата можно примерно через одинаковое количество элементов.

Двусторонняя атака является более гибкой, чем атака, в основе которой лежит парадокс задачи о днях рождения. Предположим, что элементы обоих множеств могут принимать JV возможных значений. Пусть в первом множестве содержится Р элементов, а во втором - Q элементов. Из них можно образовать PQ различных пар, в которых один элемент будет принадлежать первому множеству, а другой — второму множеству. Для каждой пары вероятность того, что значения ее элементов совпадут, равна 1/N. Мы можем ожидать возникновения коллизии, когда значение PQ/N приближается к единице. В этом случае наиболее эффективным выбором будет Р @ Q @ N. Отметим, что двусторонняя атака обладает определенной гибкостью в отношении выбора Р и Q. Иногда элементы одного множества легче получить, чем элементы второго, поэтому размер множеств может быть и неодинаков. Единственным требованием является соблюдение условия PQ @ N. Мы можем выбрать Р @ N ¹/³, a Q @ N ²/³. В приведенном выше примере злоумышленник может составить таблицу из 2⁴⁰ значений MAC и ожидать первого совпадения уже после 2²⁴ прослушанных транзакций.

⇐ Предыдущая14151617181920212223Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: