 |
Криптосистема Меркля-Хеллмана.
|
|
|
|
Предположим, что элементы открытого текста имеют в качестве своих числовых эквивалентов k -разрядные двоичные числа n.
Каждый пользователь выбирает быстрорастущий набор { v 0, …, vk – 1}, целое число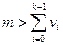 
и целое число a, такое что a < 0 < m и НОД(a, m) = 1.
После этого вычисляются b = a -1 (mod m) и k -элементный набор { Wi } = { W 0, …, Wk –1}, пределяемый равенствами Wi = avi (mod m). Пользователь держит числа { vi }, m, a и b в секрете, а набор { Wi } делает общеизвестным. Таким образом, ключом зашифрования является набор
{ W 0, …, Wk –1},
а ключом расшифрования – пара
(b, m),
которая вместе с ключом зашифрования позволяет определить набор { v 0, …, vk – 1}.
Желающий передать сообщение n = (n 0… nk – 1)2 пользователю с ключом шифрования { Wi } вычисляет
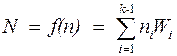
и передает это число.
Чтобы прочесть это сообщение, пользователь сначала находит s = bC:
,
поскольку bWi ≡ bav i ≡ vi (mod m). Теперь можно воспользоваться приведенным выше алгоритмом для быстровозрастающего рюкзака и найти единственное решение
(n 0… nk – 1)2 = n задачи о подмножестве { vi } с суммой равной s.
Пример. Элементы открытого текста – двоичные представления букв 26-буквенного алфавита от «A» = 0 = (00000)2 до «Z» = 25 = (11001)2.
Cекретный быстровозрастающий набор { v 0, …, vk – 1} = {2, 3, 7, 15, 31}.
Выберем m = 61, a = 17, тогда b = 18 и открытый ключ шифрования
{ W 0, …, Wk –1} = {34, 51, 58, 11, 39}.
Чтобы послать сообщение «WHY» корреспондент должен вычислить:
«W» = (10110)2 ® 51 + 58 + 39 = 148,
«H» = (00111)2 ® 34 + 51 + 58 = 143,
«Y» = (11000)2 ® 11 + 39 = 50.
N = n 1, n 2, n 3 = 148, 143, 50.
Чтобы прочитать сообщение N, сначала умножают эти числа на 18 и приводят результаты по модулю 61, получают S = s 1, s 2, s 3 = 41, 12, 46 далее, пользуясь алгоритмом для быстрорастущего рюкзака для всех si, восстанавливают сообщение
(10110)2, (00111)2, (11000)2
|
|
|
Шифрсистема Мак-Элиса.
Идея, лежащая в основе данной системы, состоит в выборе корректирующего кода, исправляющего определенное число ошибок, для которого существует эффективный алгоритм декодирования. С помощью секретного ключа этот код «маскируется» под общий линейный код, для которого задача декодирования не имеет эффективного решения.
В системе Мак-Элиса параметрами системы, общими для всех абонентов, являются числа k, n, t. Для получения открытого и соответствующего секретного ключа каждому из абонентов системы следует осуществить следующие действия:
1) Выбрать порождающую матрицу G = Gk ´ n двоичного (n, k)-линейного кода, исправляющего t ошибок, для которого известен эффективный алгоритм декодирования.
2) Случайно выбрать двоичную невырожденную матрицу S = Sk ´ k.
3) Случайно выбрать подстановочную матрицу P = Pn ´ n.
4) Вычислить произведение матриц G 1 = S · G · P.
Открытым ключом является пара (G 1, t), секретным – тройка (S, G, P).
Для того чтобы зашифровать сообщение M, предназначенное для абонента A, абоненту B следует выполнить следующие действия:
1) Представить M в виде двоичного вектора длины k.
2) Выбрать случайный бинарный вектор ошибок Z длиной n, содержащий не более t единиц.
3) Вычислить бинарный вектор C = M · GA + Z и направить его абоненту A.
Получив сообщение C, абонент A вычисляет вектор C 1 = C · P -1, с помощью которого, используя алгоритм декодирования кода с порождающей матрицей G, получает далее векторы M 1 и M = M 1 · S -1.
В качестве кода, исправляющего ошибки в системе Мак-Элиса, можно использовать код Гоппы. Известно, что для любого неприводимого полинома g (x) степени t над полем GF (2 m) существует бинарный код Гоппы длины n = 2 m и размерности k ≥ n – mt, исправляющий до t ошибок включительно, для которого имеется эффективный алгоритм декодирования. В настоящее время не известны эффективные алгоритмы дешифрования системы Мак-Элиса, использующей код Гоппы, при правильном выборе параметров системы.
|
|
|
Рекомендуемые параметры этой системы - n = 1024, t = 38, k > 644 – приводят к тому, что открытый ключ имеет размер около 219 бит, а длина сообщения увеличивается при шифровании примерно в 1,6 раза, в связи с чем данная система не получила широкого распространения.
Контрольные вопросы
1. Почему операции для криптографических преобразований должны обладать свойством замкнутости?
2. Приведите случаи, при которых функция Эйлера легко вычислима.
3. В чем различие между кольцом вычетов по модулю натурального числа и простым конечным полем?
4. Для чего используется расширенный (обобщенный) алгоритм Евклида?
5. Для решения какого вида систем сравнений используется китайская теорема об остатках?
6. В чем различие между символами Лежандра и Якоби?
7. Назовите два способа извлечения квадратных корней в простом конечном поле?
8. Может ли в криптосистеме RSA шифрующая экспонента быть четной?
9. Какие требования к модулю P предъявляются в криптосистеме Эль-Гамаля?
10. Сколько вариантов расшифрования сообщения в криптосистеме Рабина?
|
|
|
