Слабые моменты реализации RSA.

Разделенный модуль: Поскольку арифметика остатков – дорогое удовольствие с точки зрения компьютера, весьма заманчиво разработать систему шифрования, в которой пользователи разделяют общий модуль N, но применяют различные открытые и закрытые экспоненты (E_i, d_i).

Одна из причин, побуждающая это делать, - ускорить алгоритмы зашифрования и расшифрования в аппаратных средствах, специально настроенных на определенный модуль N. Однако это неудачная идея, поскольку пасует перед двумя типами нападающих: внутреннего, то есть законного пользователя системы, и внешнего.

Предположим, что нападающим является один из законных клиентов криптосистемы, скажем пользователь номер 1. Он может найти значение секретной экспоненты пользователя 2 – d ₂. Сначала он вычисляет p и q по известному ему d ₁. Затем злоумышленник находит

j (N) = (p – 1)(q – 1) и, наконец, при помощи расширенного алгоритма Евклида раскрывает значение d ₂ по формуле

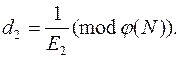
Предположим, что теперь атакующий не принадлежит к пользователям криптосистемы, использующей общий модуль. Допустим, происходит рассылка одинакового (допустим циркулярного) сообщения m двум клиентам криптосистемы, открытые ключи которых

(N, E ₁) и (N, E ₂).

Противник, нападающий извне, видит зашифрованные сообщения С ₁ и C ₂, где

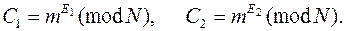
Он может вычислить

и восстановить сообщение m по следующей схеме:

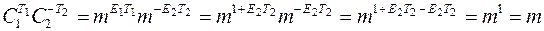
Пример. N = N ₁ = N ₂ = 18923, E ₁ = 11 и E ₂ = 5.

Предположим, что перехвачены шифртексты

C ₁ = 1514 и C ₂ = 8189,

соответствующие одному открытому тексту m. Тогда противник вычисляет T ₁ = 1 и T ₂ = 2, после чего раскрывает исходную информацию:

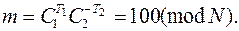
Вывод. При использовании общего модуля N любой законный пользователь системы может восстановить секретную экспоненту d другого пользователя, а внешний противник сможет читать циркулярные сообщения m.

Малые шифрующие экспоненты:

Иногда в криптосистемах RSA с целью экономии затрат на шифрование используются небольшие шифрующие экспоненты E. Это тоже создает дополнительные проблемы, связанные с криптостойкостью. Предположим, что есть три пользователя с различными модулями шифрования

N ₁, N ₂ и N ₃

и одинаковой шифрующей экспонентой E = 3. Пусть некто посылает им одно сообщение m, зашифрованное тремя разными открытыми ключами. Нападающий видит три криптограммы:

C ₁ = m ³ (mod N ₁),

C ₂ = m ³ (mod N ₂),

C ₃ = m ³ (mod N ₃)

и с помощью китайской теоремы об остатках находит решение системы

{ X = C_i (mod N_i)| i = 1, 2, 3}

в виде

X = m ³ (mod N ₁ N ₂ N ₃).

Но поскольку m ³ < N ₁ N ₂ N ₃, целые числа X и m ³ должны совпадать. Поэтому, вычисляя обычный кубический корень из X, нападающий раскрывает сообщение m.

Пример.

N ₁ = 323, N ₂ = 299, N ₃ = 341

и перехваченные сообщения

C ₁ = 50, C ₂ = 299, C ₃ = 1,

Чтобы восстановить исходное сообщение m, находим решение системы

X = 300763 (mod N ₁ N ₂ N ₃),

после чего извлекаем обычный кубический корень

m = X ^1/3 = 67.

Вывод. При использовании малой шифрующей экспоненты E противник может восстановить циркулярное сообщение m для E пользователей.

Обе вышеуказанные атаки позволяют раскрыть текст, не прибегая к разложению на множители. Наиболее важный вывод из них – необходимость дополнять оригинальные сообщения случайными цифрами перед их зашифрованием.

 

При практической реализации RSA необходимо решить следующие задачи:

1. Генерация больших простых чисел p и q с проверкой выполнения соответствующих требований к ним.

2. Выбор экспонент e и d с соблюдением соответствующих требований.

3. Реализация операции вычисления x^y (mod n).

 

Генерация большого простого числа:

1) Сгенерировать случайное n -битовое число p.

2) Установить старший и младший бит равными 1. (Старший бит гарантирует требуемую длину простого числа, а младший – обеспечивает его нечетность).

3) Убедиться, что p не делится на малые простые числа: 3, 5, 7, 11 и т.д. Во многих практических реализациях проверяется делимость p на все простые числа, меньшие 256. Наиболее надежна проверка делимости на все простые числа, меньшие 2000. Эти проверки можно выполнить на основе массива этих простых чисел.

4) Выполнить тест простоты Рабина-Миллера для некоторого случайного числа a. Если p проходит тест, сгенерировать другое случайное число a и повторить тест. Для ускорения проверки можно выбирать относительно небольшие значения a. Выполнить тест минимум пять раз. Если p не проходит один из тестов, то перейти к шагу 1).

Другой путь – не генерировать случайное число p в каждом тесте, а последовательно перебирать все нечетные числа, начиная со случайно выбранного числа, пока не найдется простое число.

Тест Рабина-Миллера:

Выбрать для тестирования число p. Вычислить b – число делений p – 1 на 2 (то есть 2 ^b – это наибольшая степень числа 2, на которую делится p – 1). Затем вычислить m, такое, что p = 1 + 2 ^b · m.

1) Выбрать случайное число a, меньшее p.

2) Установить j = 0 и z = a^m mod p.

3) Если z = 1 или если z = p – 1, то p проходит тест и может быть простым числом.

4) Если j > 0 и z = 1, то p не относится к простым числам.

5) Установить j = j + 1. Если j < b и z ¹ (p – 1), установить z = z ² mod p и вернуться к шагу 4). Если z = p – 1, то p проходит тестирование и может быть простым числом.

6) Если j = b и z ¹ (p – 1), то p не относится к простым числам.

Выбор экспонент e и d:

1) Так как единственное требование к e – отсутствие общих множителей с числом φ (n) = (p - 1) · (q - 1), то логично выбирать небольшое e легко разложимое на простые множители и осуществлять проверку делением φ (n) на множители e. Либо выбирать простое e. Неплохо также выбирать e с минимальным количеством единиц в двоичном представлении, что ускорит операцию возведения в степень, реализованную следующим алгоритмом.

2) Так как очевидно, что d = e ^-1(mod p), то d находим при помощи расширенного алгоритма Евклида.

Алгоритм вычисления x^y (mod n).

1) Представим y в двоичной системе счисления y = y ₀2 ^r + … + y_{r -1}2 + y_r, где y_i, цифры в двоичном представлении равные 0 или 1, y ₀ = 1.

2) Положим x ₀ = x и затем для i = 1,…, r вычислим

.

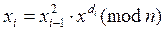3) x_r есть искомый вычет x^y (mod n).

Криптосистема Эль-Гамаля.

Односторонняя функция - возведение в степень с фиксированным модулем P и основанием G.

H = G^x (mod P)

Обратная задача – задача дискретного логарифмирования

x = ind _{G , P} H

является сложной.

Здесь опишем шифрование по Эль-Гамалю, использующее конечные поля. Существует и аналогичная система на эллиптических кривых.

В отличие от RSA, в алоритме Эль-Гамаля существуют некоторые открытые параметры, которые могут быть использованы большим числом пользователей. Они называются параметрами домена и выглядят следующим образом:

- P – «большое простое число», то есть число, насчитывающее около 1024 бит, такое, что P – 1 делится на другое, «среднее простое число» Q, лежащее неподалеку от 2¹⁶⁰.

- G – элемент мультипликативной группы поля 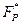, порядок которой, как мы знаем делится на Q, причем

G ^{( P – 1)/ Q} (mod P) ≠ 1.

Все параметры домена, то есть P, Q и G, выбираются таким образом, чтобы элемент G ^{( P – 1)/ Q} был образующей абелевой группы A порядка Q. Информация об этой группе открыта и используется большим числом пользователей.

После выбора параметров домена определяют открытый и закрытый ключи. Закрытым ключом может априори быть любое натуральное число x, а открытый ключ получается по следующей формуле:

H = G^x (mod P).

Обратите внимание на то, что каждый из пользователей RSA должен генерировать два больших простых числа для определения ключевой пары, что является довольно громоздкой задачей, а в системе Эль-Гамаля для построения ключевой пары достаточно найти какое-нибудь случайное число и сделать сравнительно несложные вычисления в арифметике остатков.

Сообщение в этой ситеме представляется ненулевым элементом поля 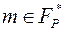. Для его шифрования поступают следующим образом:

- генерируют случайный эфемерный ключ k,

- вычисляют C ₁ = G^k,

- находят C ₂ = m · H^k,

- выдают получившийся шифртекст в виде пары С = (С ₁, С ₂).

Заметим, что при каждом шифровании применяется свой кратковременный ключ k. Поэтому, шифруя одно сообщение дважды, мы получаем разные шифртексты.

Чтобы расшифровать пару данных С = (С ₁, С ₂), производят следующие преобразования:

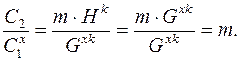
Пример. Q = 101, P = 809 и G = 3.

Легко проверить, что Q действительно делит число P – 1, а порядок элемента G в группе 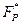делится на Q. Порядок элемента G равен 808, поскольку

3⁸⁰⁸ = 1 (mod P),

и ни при каких меньших степенях такого равенства не получается.

В качестве пары открытого и закрытого ключа выберем

x = 68 и H = G^x = 3⁶⁸ = 65 (mod P).

Допустим, нам нужно зашифровать сообщение, численное представление которого равно

m = 100. Поступаем следующим образом.

- Генерируем случайный эфемерный ключ k = 89.

- Находим С ₁ = G^k = 3⁸⁹ = 345 (mod P).

- Получаем С ₂ = m · H^k = 100 · 65⁸⁹ = 517 (mod P).

- Отправляем шифртекст C = (345, 517).

Адресат сможет восстановить текст, делая также вычисления:

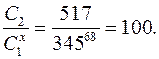
Последнее равенство получается чуть более сложно, чем в вещественных числах: сначала число 345 возводится в степень 68 по модулю 809, вычисляется мультипликативный обратный к результату по этому же модулю, а затем найденный обратный умножается на 517.

Криптосистема Рабина.

Система базируется на трудности задачи факторизации больших целых чисел, а точнее на трудности извлечения квадратного корня по модулю составного числа N = p · q.

Эти задачи эквивалентны:

- зная простые делители числа N, можно легко извлекать корни по модулю N,

- умея извлекать корни по модулю N, можно легко разложить N на составные множители.

Такую систему можно считать в некотором отношении более криптостойкой, чем RSA. Процесс шифрования в системе Рабина происходит намного быстрее, чем практически в любой другой криптосистеме с открытым ключом. Однако, не смотря на эти преимущества, система Рабина используется все же реже чем RSA.

Выбираются два простых числа p и q, удовлетворяющие условию

p = q = 3 (mod 4).

Такой специальный вид чисел сильно ускоряет процедуру извлечения корней по модулю p и q. Закрытым ключом системы является пара

(p, q).

Для определения соответствующего открытого ключа берут произведение N = p · q и генерируют случайное целое число B Î {0, …, N – 1}. Открытый ключ это пара

(N, B).

Для шифрования сообщения m в алгоритме Рабина вычисляют

C = m (m + B) (mod N).

Таким образом, шифрование состоит из операции сложения и умножения по модулю N, что обеспечивает более высокую скорость шифрования, чем в RSA, даже если в последней выбирают небольшую шифрующую экспоненту.

Расшифрование в этом алгоритме гораздо более сложное. По существу нужно вычислить

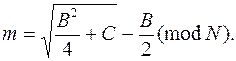
На первый взгляд здесь не требуется никакой секретной информации, но, очевидно, для извлечения корней по модулю N очень и очень полезно знать разложение N на простые множители. Поскольку N – произведение двух простых чисел, существует четыре возможных квадратных корня из числа по модулю N. Поэтому при расшифровании получается четыре возможных варианта открытого текста. Чтобы выбор был более определенным, стоит к открытому тексту добавлять некую избыточную информацию.

Объясним, почему при расшифровании мы действительно получаем m. Напомним, что шифртекст имеет вид

C = m (m + B) (mod N).

поэтому

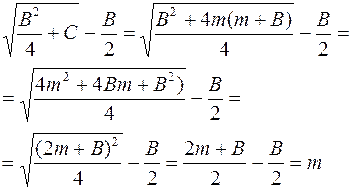
Конечно предполагаем, что мы выбрали правильный корень из четырех.

Пример. Открытый и закрытый ключи имеют вид:

- p = 127, q = 131,

- N = 16637 и B = 12345.

Для шифрования сообщения m = 4410 вычисляем

C = m (m + B) (mod N) = 4633.

При обратной операции сначала находим

T = B ²/4 + C (mod N) = 1500,

а затем извлекаем квадратные корни из T по модулю p и q:

После этого, применяя китайскую теорему об остатках к паре

±22 (mod p) и ±37 (mod q),

находим квадратный корень из T по модулю N:

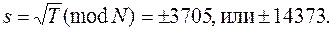
Четыре варианта расшифрования

4410, 5851, 15078, или 16519

получаются из формулы

.

 

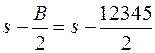Рюкзачные криптосистемы.

Задача об укладке рюкзака. Задано множество { v_i } из k натуральных чисел и целое число S.

Требуется найти такое k -разрядное число n = (n_{k – 1} n_{k – 2}… n ₁ n ₀)₂ (где n_i Î {0, 1} суть значения разрядов в двоичной записи чиcла n), что , если такое n существует.

В зависимости от набора { v_i } и числа S, такого решения может не быть вообще, решений может быть несколько или решение будет единственным. Такая задача является сложной.

Частный случай – задача об укладке быстровозрастающего рюкзака. Это случай, когда величины v_i, будучи упорядочены в порядке возрастания, обладают тем свойством, что каждое число больше суммы всех предыдущих.

Такая задача имеет эффективный алгоритм решения:

1. Положим W = S и j = k.

2. Начиная с n_{j – 1} и последовательно уменьшая j, полагаем все n_j = 0 до тех пор, пока не придем к первому такому значению j (обозначим его через i ₀), что 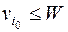. Положим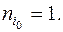

3. Заменим W на 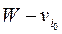, положим j = i ₀ и, если W > 0, то переходим к шагу 2.

4. Если W = 0, то цель достигнута. Если W > 0 и все оставшиеся v_i больше W, то ясно, что решения n = (n_{k – 1} n_{k – 2}… n ₁ n ₀)₂ задачи не существует. Если решение есть, то оно единственное.

Пример. Набор {2, 3, 7, 15, 31} является быстрорастущим набором, а S = 24. Тогда проходя пятерку значений справа налево, мы видим, что n ₄ = 0 (31 > 24), n ₃ = 1 (15 < 24 и в этот момент заменяем 24 на 24 – 15 = 9), n ₂ = 1 (7 < 9 и в этот момент заменяем 9 на 9 – 7 = 2), n ₁ = 0 (3 > 2), n ₀ = 1 (2 = 2). Таким образом, получаем n = (01101)₂ = 13.

⇐ Предыдущая9101112131415161718Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: