Глава 6. Функции нескольких переменных и многомерные пространства.

 

§1. Основные понятия.

Приведем примеры функций нескольких переменных:

а) объем параллелепипеда: V = abc, где a,b,c – его длина, ширина и высота;

б) сила гравитационного притяжения между телами: , где m₁ и m₂ – массы тел, R – расстояние между телами, g - гравитационная постоянная.

Это примеры функций трех переменных. Введем понятие функции n переменных на примере пространства товаров.

Будем считать, что имеется n различных товаров. Количество i – го товара обозначим x_i (i = 1,2,... n). Тогда набор товаров обозначим X = (x₁, x₂,..., x_n) – его можно рассматривать как n – мерный вектор. Множество всех наборов товаров {X} называется пространством товаров. Векторы Х называются элементами этого пространства. Любые два набора X₁ = (x₁¹, x₂¹,..., x_n¹) и X₂ = (x₁², x₂²,..., x_n²) можно сложить Х₁ + Х₂ по правилу сложения векторов и умножить любой набор товаров на любое неотрицательное число, последнее означает безграничную делимость товаров, т.е. товары «устроены» наподобие сахарного песка, а не автомобилей. Если в пространстве для всех его элементов определены операции сложения и умножения на число со всеми своими свойствами, то такое пространство называется линейным (Rⁿ). Таким образом, пространство товаров является линейным.

Пусть каждый товар имеет цену p_i (i = 1,2,... n, p_i > 0). Тогда вектор P = (p₁,p₂,_,...,p_n) – называется вектором цен. Набор товаров Х и вектор цен Р имеют одинаковую размерность. Тогда их скалярное произведение PX = p₁x₁ + p₂x₂ +... +p_nx_n есть число, которое называется ценой набора или его стоимостью и обозначается С(Х). Если в линейном пространстве определена операция скалярного произведения, то такое пространство называется евклидовым (Eⁿ). Пусть вектор цен известен, т.е. цены p₁,p₂,_,...,p_n – данные (фиксированные) величины, тогда стоимость набора товаров есть функция n неизвестных: С(Х) = p₁x₁ + p₂x₂ +... +p_nx_n.

Приведем примеры многомерных функций, используемых в экономике (их одномерные аналоги мы уже рассматривали).

Функция полезности u(X) = u(x₁, x₂,..., x_n) – субъективная числовая оценка данным индивидом полезности набора товаров Х = (x₁, x₂,..., x_n).

Функция издержек C(Y) = C(y₁, y₂,... y_n) – зависимость издержек С от объемов выпускаемой продукции Y = (y₁, y₂,... y_n).

Производственная функция y = F(X) = F(x₁, x₂,..., x_n) - зависимость объема выпускаемой продукции y от объемов перерабатываемых ресурсов Х = (x₁, x₂,..., x_n). Наиболее известная производственная функция – функция Кобба-Дугласа:

y = AK^aL^1-a, где A,a - неотрицательные константы, K – объем вкладываемого в производство капитала, L – объем вкладываемых трудовых ресурсов.

Определение. Если каждому вектору Х = (x₁, x₂,..., x_n) из множества D, являющегося подмножеством евклидова пространства Еⁿ, по некоторому правилу (закону) f поставлено в соответствие одно и только одно число yÎ E Ì R, то говорят, что на множестве D задана (определена) функция n переменных: y = f(x₁, x₂,..., x_n) или y = f(X).

При этом x₁, x₂,..., x_n – независимые переменные (аргументы), y – зависимая переменная (функция).

Множество D – называется областью определения функции; множество значений, принимаемых функцией E, называется областью изменения функции.

Введем понятие предела функции нескольких переменных. С этой целью рассмотрим топологию n – мерного пространства.

Топология пространства – это вопрос о том, как оно устроено с точки зрения предельного перехода. Топология евклидова пространства Е^п очень похожа на топологию пространства действительных чисел R, только модуль числа х заменяется длиной вектора Х = (x₁, x₂,..., x_n): . Основные определения:

Определение. e (эпсилон) – окрестностью точки AÎ Е^п называется множество всех точек X, для которых выполняется условие 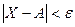, т.е. это n – мерный шар радиусом e и центром в точке A.

Определение. Точка A называется внутренней точкой множества DÌ Е^п, если для этой точки существует e - окрестность, все точки которой принадлежат множеству D.

Определение. Точка A называется граничной точкой множества DÌ Е^п, если любая ее e - окрестность содержит как точки множества D, так и точки пространства, не принадлежащие ему.

Определение. Множество D Ì Е^п называется открытым, если все точки этого множества – внутренние.

Определение. Множество D Ì Е^п называется замкнутым, если все граничные точки этого множества принадлежат ему.

Определение. Множество D Ì Е^п называется ограниченным, если найдется такое число К, что для всех ХÎ D выполняется условие êХê£ К.

 

Можно рассмотреть последовательность элементов евклидова пространства:

Х₁, Х₂,... Х_n... = {X_n}.

Определение. Элемент A Î Rⁿ называется пределом последовательности {X_n}Ì Е^п, если для любого e > 0 найдется такой номер N, что для всех номеров n > N выполняется условие . Обозначается: .

Определение. Число а называется пределом функции y = f(X) при Х ® А (Х и А Î Е^п), если для любого e > 0 найдется такое d > 0, что для всех Х, для которых выполняется неравенство следует выполнение условия . Обозначается: .

Определение. Функция y = f(X) называется непрерывной в точке А (А Î Е^п), если она определена в этой точке и .

Определение. Пусть a(Х) – функция, определенная в евклидовом пространстве (Х Î Е^п). Тогда величина a называется бесконечно малой в точке А (А Î Е^п), если .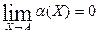

Основные свойства пределов и непрерывности, бесконечно малых величин, рассмотренные ранее для функции одной переменной, справедливы (с соответствующими поправками) для функции многих переменных. Это позволяет определить понятия дифференциального исчисления для числовых функций нескольких переменных, аналогично тому, как это было сделано для функции одной переменной.

 

⇐ Предыдущая567891011121314Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: