 |
Производная по направлению, градиент функции.
|
|
|
|
Частные производные функции y=f(x1,x2..xn) по переменным x1, x2... xn выражают скорость изменения функции по направлению координатных осей. Например, 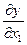 есть скорость изменения функции по х1 – то есть предполагается, что точка, принадлежащая области определения функции, перемещается лишь параллельно оси ОХ1 , а все остальные координаты остаются неизменными. Однако, можно предположить, что функция может изменяться и по какому-нибудь другому направлению, не совпадающему с направлением какой либо из осей.
есть скорость изменения функции по х1 – то есть предполагается, что точка, принадлежащая области определения функции, перемещается лишь параллельно оси ОХ1 , а все остальные координаты остаются неизменными. Однако, можно предположить, что функция может изменяться и по какому-нибудь другому направлению, не совпадающему с направлением какой либо из осей.
Рассмотрим функцию трех переменных: u=f(x,y,z).
Зафиксируем точку М0(x0,y0,z0) и какую-нибудь направленную прямую (ось) l, проходящую через эту точку. Пусть М(x,y,z) - произвольная точка этой прямой и ê М0М ê- расстояние от М0 до М.
Du = f (x,y,z) – f(x0,y0,z0) – приращение функции в точке М0.
Найдем отношение приращения функции к длине вектора  :
:

Определение. Производной функции u = f (x,y,z) по направлению l в точке М0 называется предел отношения приращения функции к длине вектора ê М0М ê при стремлении последнего к 0 (или, что одно и то же, при неограниченном приближении М к М0):
 (1)
(1)
Эта производная характеризует скорость изменения функции в точке М0 в направлении l.
Пусть ось l (вектор М0М)образует с осями OX, OY, OZ углы  соответственно.
соответственно.
Обозначим x - x0 =  ;
;
y - y0 =  ;
;
z - z0 =  .
.
Тогда вектор М0М = (x - x0, y - y0, z - z0)=  и его направляющие косинусы:
и его направляющие косинусы:
 ;
;
 ;
;
 .
.
Отсюда получаем следующие выражения для Dx, Dy, Dz:

 (2)
(2)
Полное приращение функции  в точке М0:
в точке М0: 
можно представить в виде:
 (3), где
(3), где

Подставим выражения (2) в (3):
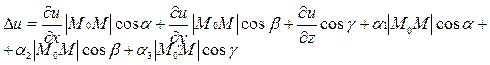
Найдем отношение 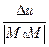 :
:

Перейдем к пределу при ê М0М ê ® 0:

 (4).
(4).
(4) – формула для вычисления производной по направлению.
Конечно, направление может быть задано просто соответствующим вектором. Рассмотрим вектор, координатами которого являются частные производные функции u=f(x, y, z) в точке М0:
|
|
|

grad u - градиент функции u=f(x, y, z) в точке М(x, y, z)
Рассмотрим единичный вектор по направлению l -  - это вектор, длина которого равна 1,а направление совпадает с направлением оси l.
- это вектор, длина которого равна 1,а направление совпадает с направлением оси l.
Тогда производная функции u=f(x, y, z) по направлению l может быть представлена как скалярное произведение( ):
):
 .
.
Следовательно, производная функции u=f(x, y, z) по данному направлению l есть скалярное произведение градиента функции на единичный вектор этого направления.
Пусть j - угол между grad u и l, тогда:
 (5).
(5).
Производная  функции u=f(x, y, z) по направлению l равна проекции вектора grad u на ось l.
функции u=f(x, y, z) по направлению l равна проекции вектора grad u на ось l.
Свойства градиента:
- Производная функции u=f(x, y, z) в данной точке М(x, y, z) по направлению l имеет наибольшее значение, если направление l совпадает с направлением градиента функции в этой точке.
- Наибольшее значение производной функции u=f(x, y, z) по заданному направлению в данной точке М(x, y, z) равно длине градиента функции в этой точке:
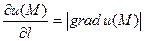 .
.
Вывод: длина градиента функции u=f(x, y, z) – есть наиболее возможное значение 
 в данной точке М(x, y, z), а направление вектора grad u совпадает с направлением вектора, выходящего из точки М, вдоль которого функция меняется быстрее всего. То есть, направление градиента функции grad u - есть направление наискорейшего возрастания функции.
в данной точке М(x, y, z), а направление вектора grad u совпадает с направлением вектора, выходящего из точки М, вдоль которого функция меняется быстрее всего. То есть, направление градиента функции grad u - есть направление наискорейшего возрастания функции.
 §6. Частные производные высших порядков.
§6. Частные производные высших порядков.
Частные производные  , i = 1,2,...,n называют частными производными первого порядка. Их можно рассматривать как функции от X=(x1,x2,... xn)
, i = 1,2,...,n называют частными производными первого порядка. Их можно рассматривать как функции от X=(x1,x2,... xn)  . Эти функции могут иметь частные производные, которые называются частными производными второго порядка. Они определяются и обозначаются следующим образом:
. Эти функции могут иметь частные производные, которые называются частными производными второго порядка. Они определяются и обозначаются следующим образом:
 (1),
(1),
где i = 1, 2,..., n и k = 1, 2,..., n.
Если i ¹ k, то частная производная (1) называется смешанной частной производной второго порядка. Если i = k, то частная производная второго порядка обозначается следующим образом:
|
|
|
 (2).
(2).
Аналогично определяются частные производные третьего, четвертого и т.д. порядков.
Функция y = f (x1,x2…xn) называется m раз дифференцируемой в точке М0(x10, x20...,xn0), если все её частные производные (m-1) -го порядка являются дифференцируемыми функциями в этой точке.
Пример:
Найти частные производные второго порядка функции: z= x3 - x2y3 + x + y4.
z’x = 3x2 - 2xy3 + 1; z’y= - x23y2 + 4y3;
z’xx = 6x - 2y3; z’’yx = - 2x3y2 = - 6xy2;
z’’xy= - 2x3y2 = - 6xy2; z’’yy= -x26y +12y2.
Оказалось, что z’’xy = z’’yx. Это не случайно.
Имеет место следующая теорема (без доказательства).
Теорема Шварца
Если функция y = f (X) дифференцируема m раз в точке M (x1, x2 .. xn), то смешанные производные m- го порядка в этой точке, отличающиеся лишь порядком дифференцирования, равны между собой.
В частности, для функции z = f (x,y) имеем  .
.
|
|
|


