Главная | Обратная связь | Поможем написать вашу работу!

Основные расчетные гидрологические характеристики водотоков.

В соответствии с требованиями СП 33-101-2003 (Определение …, 2004). для обоснования параметров расчетных формул выполнялся пространственный анализ основных гидрологических характеристик с использованием данных наблюдений на гидрометрических постах района исследований. В процессе работы над отчетом были собраны ряды минимального и годового стока по рекам района за весь период наблюдений.

В расчетах были использованы данные наблюдений по 1 посту. Основные сведения по этому пункту представлены в таблице 6.8.3

Таблица 6.8.3 – Основные морфометрические характеристики реки–аналога для района изысканий

Река - пост	F,км²	L,км	J,‰	H,м	f_оз,%	f_б,%	f_л,%
р. Малый Ыллымах – г.п. Соболиный	30,3	8,5	-		<1	<5

На первом этапе производился выбор наиболее адекватной модели для описания вероятностной структуры гидрологических рядов по каждому виду стока. В качестве возможных моделей рассматривались: модель случайной величины и модель простой цепи Маркова (авторегрессия первого порядка). В качестве критерия на соответствие модели случайной величины использовался критерий значимости коэффициента автокорреляции.

Гипотеза о случайности ряда не опровергалась, если выполнялось неравенство:

, (4.1)

где: r (1)	–	коэффициент автокорреляции ряда;
t ₂_a%	–	нормированная ордината нормального распределения при уровне значимости 2a = 5 %;
s_r ₍₁₎	–	среднеквадратическая ошибка коэффициента автокорреляции, определяемая по формуле (4.2).

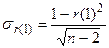, (4.2)

где: n – длина ряда.

Учитывая большую погрешность выборочных коэффициентов автокорреляции, решение о принятии той или иной вероятностной модели принималось на основе группового анализа рядов в пределах гидрологически однородного района.

На втором этапе проводилась проверка рядов на однородность. Проверка рядов на однородность проводилась с использованием критериев Фишера и Стьюдента. Теоретические значения статистик Фишера и Стьюдента определялись по таблицам (Пособие…, 1984), с учетом районного значения коэффициента автокорреляции. Проверка проводилась при уровне значимости 2 a = 5 %. Гипотеза об однородности рядов не опровергалась, если выполнялись следующие условия:

F^* < F₂_a, (4.3)

t ^* < t₂_a, (4.4)

где: F^, t ^	–	эмпирические значения статистик, соответственно Фишера и Стьюдента;
F₂_a, t₂_a	–	теоретические значения статистик, соответственно Фишера и Стьюдента, при уровне значимости 2 a = 5 %.

На третьем этапе производился расчет оценок параметров распределения методом моментов. В том случае, когда коэффициент вариации (C_v) превышал 0,6, параметры пересчитывались методом наибольшего правдоподобия.

Если для описания вероятностной структуры гидрологических рядов использовалась модель авторегрессии первого порядка, значение C_v корректировалось по формуле

(4.5)

где: n	–	длина ряда;
	–	смещенная оценка C_v (т. е. без учета автокорреляции.);
a ₁… a ₆	–	коэффициенты, определяемые по приложению Б.1 (Определение …, 2004)

Учитывая большую погрешность расчета коэффициента асимметрии (C_s), значение отношения C_s/C_v для каждого вида стока принималось постоянным для всего исследуемого района.

При аппроксимации эмпирических кривых обеспеченностей в качестве аналитической кривой для всех видов стока использовалась кривая Крицкого-Менкеля (трехпараметрическое гамма-распределение).

Среднегодовые расходы воды. Обработка рядов годового стока реки-аналога проводилась в соответствии с методикой, в результате которой были получены оценки статистических параметров, приведенные в таблице 6.8.4.

Таблица 6.8.4. – Статистические параметры годового стока реки – аналога

Река – пункт	Площадь водосбора, км²	Среднегодовой расход, м²/с	Среднегодовой модуль, л/с км²	C_v
р. Малый Ыллымах – г.п. Соболиный	30.3	0.34	11.2	0.40

Учитывая большую погрешность коэффициента асимметрии, значение отношения Cs/Cv принималось осредненным для всего рассматриваемого района: Cs/Cv = 6.0 (с округлением до десятых).

Для неизученных рек района изысканий модуль годового стока принят равным по региональной зависимости модуля стока от средней высоты водосбора, приведенной на рисунке 6.8.1.

Рис. 6.8.1.– Расчетная зависимость средней высоты водосбора модуля стока.

Погрешности расчета среднего значения в большинстве случаев не превышают 10 %, а погрешности расчета коэффициента вариации – 15 %, таким образом, полученные числовые характеристики являются надежными, при этом эмпирические кривые обеспеченностей достаточно хорошо согласуются с аналитическими кривыми.

Расчетные значения среднегодовых расходов воды реки-аналога района представлены в таблице 6.8.5.

Таблица 6.8.5.– Среднегодовые расходы воды (м³/с) расчетной обеспеченности реки–аналога

Река - пункт	Средний расход, м³/с	Средние расходы обеспеченностью, p %

р. Малый Ыллымах – г.п. Соболиный	0,34	0,82	0,59	0,51	0,40	0,31	0,26	0,21	0,19	0,17

Внутригодовое распределение стока. Внутригодовое распределение стока в районе изысканий характеризуется высокой неравномерностью в течение года: сильно выраженным весенним половодьем в сочетании с дождевыми паводками, достигающим 90 % и больше от объема годового стока, и низкой зимней меженью. Благодаря чему водность рек в весенне-летний период значительно больше, чем в зимний сезон. Зимняя межень устойчива и характеризуется постепенным уменьшением расходов воды к концу сезона. Зимой р. Малый Ыллымах перемерзает. Границы сезонов: весна – лето (май – сентябрь); осень (октябрь); зима (ноябрь – апрель). Лимитирующий период – осень – зима (октябрь – апрель), лимитирующий сезон (зима).

Типичное внутригодовое распределение стока в районе изысканий представлено на примере реки р. Малый Ыллымах – г.п. Соболиный (рис. 6.8.2.).

Рис. 6.8.2.– Внутригодовое распределение стока р. Малый Ыллымах – г.п. Соболиный в годы различной водности (%)

Данное внутригодовое распределение было использовано в качестве типового при определении характеристик стока неизученных водотоков на участке изысканий. В частности, при определении расхода, соответствующего минимальному стоку в зимний и летний периоды. Для определения типового внутригодового распределения стока водотоков, были использованы данные многолетних наблюдений по посту р. Малый Ыллымах – г.п. Соболиный, которые приведены в таблице 6.8.6.– 6.8.7.

Таблица 6.8.6.– Внутригодовое распределение стока (%) по р. Малый Ыллымах – г.п. Соболиный.

Водность	Весна - лето	Осень	Зима
V	VI	VII	VIII	IX	X	XI	XII	I	II	III	IV
Маловодный	69,7	13,8	6,03	2,54	5,45	2,47
Средний	43,3	16,3	8,47	9,16	15,3	6,87	0,62
Многоводный	29,0	14,6	10,3	15,1	22,2	6,17	1,49					1,06

Таблица 6.8.7.– Сезонное распределение стока (%) по посту р. Малый Ыллымах – г.п. Соболиный.

Водность	Весна - лето	Осень	Зима
Маловодный	97,5	2,5
Средний	92,5	6,9	0,6
Многоводный	91,2	6,2	2,6

Минимальный сток. Для оценки минимального стока района изысканий были собраны и подвергнуты статистической обработке ряды минимальных суточных зимних и летних расходов воды реки-аналога р. Малый Ыллымах – г.п. Соболиный. Результаты оценки статистических параметров и квантилей 50, 75, 90% обеспеченности приведены в таблицах 6.8.8.и 6.8.9.

Среднесуточный минимальный сток 80 % обеспеченности за летне-осенний и зимний периоды определен по картам изолиний. Для перехода от минимального стока 80 % обеспеченности к другим обеспеченностям введены переходные коэффициенты. Расчет производился по формуле:

М_р=(М_80%-а)b (4.6)

где: М_р	–	Модуль минимального стока различной обеспеченности;
М_80%-	–	Модуль минимального стока 80% обеспеченности;
a, b	–	Поправочные коэффициенты (Пособие…, 1984)

Таблица 6.8.8.– Минимальные зимние расходы воды реки–аналога

Река - пункт	F, км²	Среднесуточный расход воды с обеспеченностью, м³/сек	30-дневный расход воды с обеспеченностью, м³/сек

р. Малый Ыллымах – г.п. Соболиный.	30,3

Таблица 6.8.9.– Минимальные летне-осенние расходы воды реки–аналога

Река - пункт	F, км²	Среднесуточный расход воды с обеспеченностью, м³/сек	30-дневный расход воды с обеспеченностью, м³/сек

р. Малый Ыллымах – г.п. Соболиный.	30,3	0,095	0,046	0,020	0,15	0,074	0,024

Максимальный сток. Как показал анализ, в рассматриваемом районе максимальные годовые расходы обеспеченностью 1 % и 10 % формируются в период весеннего половодья, как на больших и средних реках, так и на малых. Ниже представлены результаты расчетов максимального расхода реки – аналога для района изысканий.

Максимальные расходы. Как показал анализ, гипотеза о соответствии рядя максимального весеннего стока модели случайной величины не опровергается. Поэтому для расчетов использовалась модель случайной величины.

Проверка ряда на однородность показала, что ряд является однородным как в отношении среднего (по критерию Стьюдента), так и в отношении изменчивости (по критерию Фишера) при уровне значимости 5 %.

Учитывая большую погрешность коэффициента асимметрии, значение отношения Cs/Cv принималось осредненным для всего рассматриваемого района: Cs/Cv = 4. Эмпирическая кривая обеспеченностей достаточно хорошо согласуются с аналитической кривой. Расчетные значения максимального расхода весеннего половодья представлены в таблице 6.8.10.

Таблица 6.8.10. – Максимальные расходы весеннего половодья (м³/с) расчетной обеспеченности реки – аналога

Река - пункт	F, км²	Средний расход, м³/с	Расходы обеспеченностью, p %

р. Малый Ыллымах – г.п. Соболиный	30,3	6,69	13,5	12,8	12,3	11,6	10,4	8,83	8,24	6,18

⇐ Предыдущая 9 10 11 12 131415 16 17 18 Следующая ⇒

Воспользуйтесь поиском по сайту: