 |
Поверхностных аКустических волн
|
|
|
|
Раздел 5. ПРИМЕНЕНИЕ ТЕОРИИ ПРОСТРАНСТВЕННЫХ СПЕКТРОВ ДЛЯ АНАЛИЗА СХЕМ оптического зондирования
поверхностных аКустических волн
5.1. Вводные замечания. Поверхностные акустические волны (ПАВ) широко используются в радиоэлектронике для построения различных устройств: линий задержки, фильтров, резонаторов, устройств обработки сигналов и т.д. В большинстве устройств используются волны Рэлея[1], которые распространяются вдоль поверхности подложки, проникая вглубь подложки на расстояние порядка длины поверхностной акустической волны Рэлея L. Длины волн Рэлея, применяемые в устройствах радиоэлектроники, обычно лежат в пределах от нескольких сотен до единиц микрон. Скорости поверхностных волн составляют несколько километров в секунду. Например, скорость ПАВ на поверхности кристаллического кварца Y -среза в Х направлении составляет V =3159 м/с. При возбуждении и распространении ПАВ на поверхности подложки образуется периодический рельеф, бегущий вдоль поверхности со скоростью волны, V. Амплитуда этого рельефа обычно невелика и составляет величину от долей до единиц ангстрем, т.е. порядка 10-10 м. Возбуждение ПАВ обычно осуществляют с помощью специальной системы электропроводящих металлических тонкопленочных электродов, расположенных на поверхности подложки, изготовленной из материала, обладающего пьезоэлектрическим эффектом. Конфигурация электродов преобразователя приведена на рис. 2.1, она напоминает две гребенки, вставленные одну в другую. Такие преобразователи называются встречноштыревыми преобразователями, сокращенно: ВШП. На электроды преобразователя подается переменное электрическое напряжение с некоторой частотой F. В промежутках между электродами ВШП возникает электрическое поле, которое вызывает деформации материала подложки между электродами первой и второй гребенок ВШП. Направление поля и направление деформаций периодически изменяет свой знак при перемене полярности напряжения, приложенного к электродам. Эти меняющиеся деформации порождают две бегущие волны, которые распространяются в противоположных направлениях, перпендикулярных линиям электродов ВШП. При движении волны поперек линий ВШП амплитуда волны может увеличиваться, если за время, равное периоду колебаний, волна пройдет расстояние, равное периоду ВШП. В этом случае происходит синфазное сложение элементарных волн от различных периодов ВШП и наращивание амплитуды волны при её движении от предыдущего периода к следующему периоду ВШП до тех пор, пока волна не выйдет за пределы ВШП. Вследствие симметрии ВШП излучает поверхностную волну в двух противоположных направлениях.
|
|
|
Максимальная амплитуда излученных волн наблюдается на резонансной частоте 
, где 
- скорость распространения поверхностной акустической волны, а 
- период структуры ВШП. Полоса пропускания ВШП, т.е. полоса частот 
, в которой амплитуды излучаемых волн не сильно отличаются от максимальной амплитуды волны, излучаемой на частоте 
, зависит от количества пар штырей ВШП, N. Приблизительная оценка величины полосы пропускания ВШП составляет:
Постановка задачиоптического зондирования. При исследованиях ПАВ была поставлена задача измерения амплитуды поверхностной волны, а также исследования распределений амплитуд на поверхности подложки. Для решения этой задачи были разработаны и применены методыоптического зондирования поверхностных акустических волн. Описание различных методов оптического зондирования можно найти в работе [10] и в обзорах [15.16]. Далее рассмотрим некоторые схемы оптического зондирования ПАВ.
|
|
|
5.2 Простая дифракционная схема оптического зондирования ПАВ. 5.2.1 Описание схемы. Простая схема, реализующая метод дифракционного зондирования, изображенная на рис. 2.1. описана в [10]. Пучок когерентного света направляется на поверхность подложки и отражается от нее. Для лучшего отражения зондирующего лазерного пучка поверхность подложки нередко покрывают тонкой пленкой металла с высоким коэффициентом отражения, например, пленкой алюминия.
В результате отражения от подложки оптическая волна получает пространственную фазовую модуляцию (ПФМ) с периодом L, бегущую в направлении распространения волны со скоростью . Модуляция образуется за счет рельефа (гофра) на поверхности, создаваемого поверхностной акустической волной. Воздействие ПАВ на оптическую волну подобно воздействию рельефной отражающей фазовой дифракционной решетки. Отличие состоит в том, что в случае гофра, созданного за счет ПАВ фазовая дифракционная решетка, образованная гофром, движется поступательно с постоянной скоростью V в направлении движении ПАВ. Движение дифракционной решетки приводит к изменению частоты дифрагированных световых волн первых порядков. Эффект изменения (сдвига) частоты световых волн первых порядков при дифракции на движущейся решетке был рассмотрен в разделе 1.8.5. Следует, однако, заметить, что при простом детектировании дифрагированных световых пучков фотодиодом эффект изменения частоты оптической волны никак не проявляется в выходном сигнале, так как выходной сигнал фотодиода пропорционален мощности светового пучка.
В результате отражения оптической волны от поверхности образуются дифракционные порядки, подобно тому, как дифракционные порядки наблюдались при дифракции когерентной оптической волны на фазовой дифракционной решетке. Метод измерения глубины модуляции основан на измерении величины мощности лазерного пучка, дифрагированного в первый порядок и сравнении её величины с мощностью зондирующего пучка или с мощностью пучка в нулевом порядке дифракции.
Рис. 5.1. Схема зондирования поверхностной акустической волны лазерным лучом
5.2.2. Расчетные соотношения. Поставим задачу: получить соотношения, с помощью которых по результатам измерений мощностей дифракционных порядков по схеме рис. 5.1., можно было бы определить амплитуду ПАВ. Запишем несколько соотношений, которые лежат в основе метода. Амплитуду пространственной фазовой модуляции световой волны при ее отражении от поверхности с рельефом на ней можно рассчитать по формуле (1.77), полученной ранее в разделе 1.8:
|
|
|
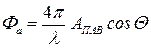, (5.1)
где 
– амплитуда поверхностного гофра, создаваемого поверхностной волной; 
– угол падения оптической волны по отношению к нормали.
Запишем выражение, описывающее функцию пространственной фазовой модуляции волнового фронта, положив, что модуляция имеет гармоническую форму, а зондирование осуществляется плоской волной.
. (5.2)
Здесь 
– пространственная частота ПАВ;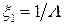 
, где 
– длина волны;
-амплитуда зондирующей волны. Фа – амплитуда пространственной фазовой модуляции, она может быть выражена через амплитуду ПАВ с помощью формулы (5.1).
На практике амплитуда ПАВ обычно очень мала, порядка (0,1¸10) × 10-10м. Вследствие этого величина амплитуды фазовой модуляции волнового фронта также очень мала, т.е. выполняется условие:
Фа << 1. (5.3)
Для того, чтобы убедиться в этом проведем оценку Фа для типичных величин амплитуд ПАВ: » (0,1¸10) × 10-10м. Для 
м. при 
:
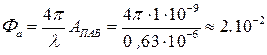радиан. 
С учетом условия (5.3) можно заменить формулу (5.2) приближенным выражением
. (5.4)
Исследуем пространственный спектр дифракционных волн. Его можно найти, если (5.4) подставить в интеграл (1.11) преобразования Фурье. В результате получим:
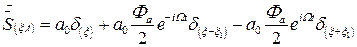. (5.5)
Здесь обозначено: 
. Величина 
– это не что иное, как частота поверхностной акустической волны, а величина 
– ее круговая частота. Выражение (5.5) записано для модели зондирования плоской волной с неограниченной апертурой, поэтомув выражении (5.5) присутствуют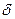 
- функции.
Если перейти от неограниченной апертуры к ограниченной щелевой апертуре пучка, то мы получим следующее выражение:
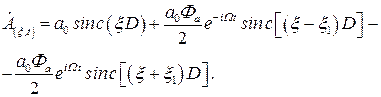(5.6)
В этом случае, пространственный спектр состоит из трех линий с конечной шириной пространственного спектра, расположенных в районе пространственных частот 
. Выражение (5.6) записано для одного измерения. В направлении оси 0x картина неоднородна, а в направлении 0y картина однородна. Соответственно пространственный спектр (5.6) неоднороден по координате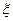 
, но однороден по координате 
|
|
|
Если зондирующий пучок имеет неоднородное распределение амплитуд в двух измерениях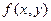 
, а его Фурье- преобразование представляется некоторой функцией 
, то выражение (5.6) примет вид:
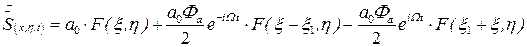(5.7)
Поясним физический смысл множителей 
и 
в выражениях (5.6) и (5.7). Для этого выражения (5.6) и (5.7) дополним множителями 
, которые ранее были опущены при переходе от полного выражения, описывающего электромагнитную волну, к сокращенной записи, которая описывает комплексную амплитуду волны. Если вновь дополнить множителем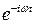 
формулы (5.6) и (5.7), то получим следующие результаты. Первый член в формуле (5.7), описывающий волну нулевого порядка дифракции, будет иметь множитель 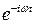, зависящий от времени. Излучение нулевого порядка имеет частоту световых колебаний w.
Второй член, описывающий дифракцию в первый порядок, будет иметь множитель 
, т.е. его зависимость от времени содержит частоту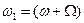 
.
Третий член, описывающий дифракцию в первый отрицательный порядок, будет иметь множитель 
, а его зависимость от времени содержит частоту 
.
Таким образом, мы видим, что в +1 и -1 порядках оптическая волна имеет сдвиг частоты на величину частоты акустической волны. Это явление сдвига частоты света может быть представлено как результат эффекта Доплера, так как излучение света происходит с движущихся возмущений, вызванных акустической волной.
Далее в схеме мы выделяем один из дифракционных порядков и направляем на фотодетектор. Сигнал с выхода фотодетектора пропорционален мощности светового излучения, попавшего на площадку фотодетектора, и, следовательно, пропорционален квадрату амплитуды световой волны. Рассмотрим соотношение мощностей отдельных составляющих в пространственном спектре. Положим, что дифракционные порядки хорошо разделяются в пространстве, т.е. выполняется условие 
. Для экспериментов применим фотодетектор с достаточно большой площадкой, захватывающей практически всю мощность излучения выбранного дифракционного порядка. В этом случае фотодетектор интегрирует излучение по координатам x и h в выбранном порядке. На рис. 5.2.схематически изображены фотодетекторы, установленные в нулевом и в первом дифракционном порядке.
Рис. 5.2. Эквивалентная схема, иллюстрирующая разделение дифракционных порядков и измерение их мощностей
Величину интегральной мощности излучения в первом и в нулевом дифракционном порядке можно рассчитать пользуясь соотношениями:
|
|
|
. (5.8)
(5.9)
Функции 
и 
, входящие в (5.8) и (5.9) имеют одинаковую форму и лишь смещены на величину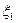 
в координатах пространственных частот. Соответственно и интегралы в (5.8) и (5.9) будут одинаковы, если пределы интегрирования имеют одинаковые конфигурации, а площадка интегрирования 
смещена относительно площадки 
на величину 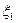. Другими словами, эти интегралы будут одинаковы, если диафрагмы в нулевом и первом дифракционном порядках одинаковы и точно установлены относительно центров дифракционных максимумов. При правильной настройке интегралы в (5.8) и (5.9) равны. Если измерить величины 
и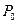 
,а затем рассчитать отношение 
, то можно определить величину 
. Отношение мощности в первом порядке дифракции к мощности в нулевом порядке дифракции составляет:
. (5.10)
Отсюда видно, что по результатам измерений величин и 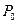мы получаем возможность рассчитать величину амплитуды волны с помощью следующего соотношения:
. (5.11)
Методика прямого дифракционного зондирования ПАВ использовалась во многих экспериментах и с ее помощью была получена ценная информация о структуре волновых полей [10]. Главный недостаток этой методики – не самая высокая чувствительность. Это объясняется тем обстоятельством, что соотношение очень мало. Так, например, если 
метра и при зондировании ПАВ применяется излучение красного гелий- неонового лазера с длиной волны l = 0,6328 мкм = 0,63.10-6 м., величина ПФМ составит: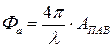 
= 2.10-3 радиан. Тогда отношение мощностей в первом и нулевом дифракционных порядках составит: 
=10-6. Если для зондирования использовать лазер с мощностью 1 мВт, то в первом порядке дифракции необходимо регистрировать мощность около 10-9 Вт. Как видно из выражения (5.10), при уменьшении амплитуды волны величина уменьшается пропорционально квадрату амплитуды волны и становится настолько малой, что возникают значительные трудности в их надежной регистрации. Практически с помощью методики, описанной в [10] проводили измерения ПАВ с амплитудой 0,1 
= 
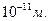
Задача измерения малой мощности светового пучка в первом дифракционном порядке осложняется еще и тем, что существует рассеяние света при отражении его от зондируемой поверхности подложки. Рассеянный свет попадает на фотодетектор и создает постоянный фототок. На фоне этого постоянного фона фототока мы должны зарегистрировать приращение фототока, которое вызвано дифракцией света на ПАВ. При этом вполне возможно, что рассеяние на неоднородностях подложки даст более сильный сигнал, чем сигнал, вызванный дифракцией света на ПАВ. Сам по себе рассеянный свет не исключает возможности измерения приращения сигнала, вызванного ПАВ, поскольку постоянный уровень сигнала можно вычесть из результата измерений. Наибольшую опасность для измерений представляют флуктуации уровня рассеянного света при изменении положения зондирующего пятна на поверхности подложки и мощности лазера. Кроме того, дополнительный постоянный ток фотодетектора вызовет повышение уровня дробовых шумов. В конечном итоге именно флуктуации мощности лазера и рассеяние света будут определять минимальный детектируемый уровень сигнала в первом порядке дифракции.
Выводы из проведенного анализа.
· С помощью изложенной методики оптического зондирования можно измерить амплитуду ПАВ. Для этого следует измерить отношение мощностей в первом и нулевом дифракционных порядках и затем провести расчет по формуле (5.11)
· Если подложку с ПАВ перемещать относительно зондирующего лазерного пучка, можно измерить распределение амплитуд ПАВ в поперечном направлении, а также исследовать, как изменяется это распределение в зависимости от изменения расстояния между областью зондирования и излучателем ПАВ.
· Диапазон длин волн ПАВ, в котором практически можно проводить измерения амплитуд ПАВ, составляет от нескольких сотен микрометров до нескольких единиц микрометров. Измерения принципиально невозможны при 
, так как при этих условиях дифракционные порядки отсутствуют.
|
|
|
