 |
Модель зондирования ПАВ с опорной дифракционной решеткой, отделенной от звукопровода.
|
|
|
|
Если ОДР расположена на поверхности, она может создавать помехи движению ПАВ. Чтобы исключить влияние ОДР на распространение ПАВ можно расположить ОДР на некотором расстоянии от поверхности звукопровода ПАВ. При этом возможны три варианта схемы зондирования, изображенные на рис.5.5.
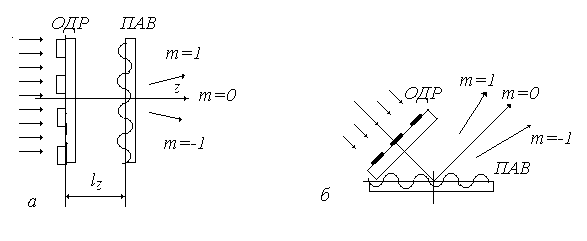
Рис.5.5. Три схемы зондирования ПАВ с опорной дифракционной решеткой, отделенной от звукопровода:
а- схема зондирования на просвет, когда подложка прозрачна для зондирующего излучения.
б- схема зондирования с отражением лазерного пучка от звукопровода и с однократным прохождением оптического пучка через ОДР.
в- схема зондирования с отражением лазерного пучка и с двукратным прохождением оптического пучка через ОДР.
Далее мы будем рассматривать наиболее простую модель, которая пригодна для описания схемы 5.5а и схемы 5.5б. Эквивалентная сема для анализа представлена на рис.5.6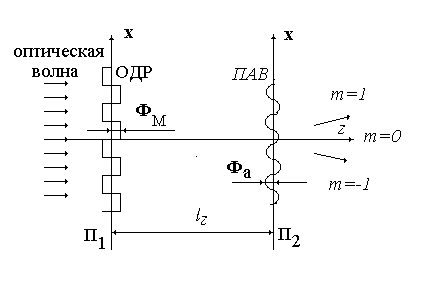 
Рис.5.6. Эквивалентная схема взаимодействия оптической волны с ОДР и ПАВ,при условии, что они разделены в пространстве расстоянием 
. В качестве ОДР применена решетка фазового типа. На рисунке отображена форма фазовой пространственной модуляции.
5.4.1. Анализ схемы с ОДР амплитудного типа, отделенной от звукопровода.
Пусть в плоскости 
расположена неподвижная решетка амплитудного типа с гармонической функцией пропускания:
, (5.57)
Где m- коэффициент глубины модуляции,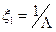 
- пространственная частота ОДР, а 
- период ОДР.
В плоскости П2 расположена движущаяся фазовая решетка с малой глубиной модуляции, функция пропускания которой выражается формулой:
(5.58)
Эта формула подобна формуле (5.13), но для сокращения мы положили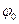 
=0
Здесь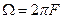 
- круговая частота ПАВ.
Далее для анализа схемы применим теорию пространственных спектров. Как и в предыдущих задачах, мы будем проводить расчеты, предполагая, что зондирующая волна – плоская и неограниченная.
|
|
|
Пространственный спектр оптической волны после прохождения ОДР, находящейся в плоскости П1 обозначим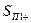 
. Выполнив преобразование Фурье функции (5.57) получим:
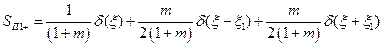(5.59)
Далее оптическая волна распространяется от плоскости П1 к плоскости П2 в свободном пространстве. При этом различные компоненты пространственного спектра получают различные фазовые задержки. Функция передачи свободного пространства была рассмотрена в разделе 1, она имеет вид:
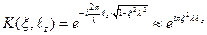(5.60)
Будем проводить дальнейшие расчеты пользуясь приближенной формулой 5.60, которая применима при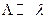 
, т.е. при 
.
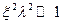Умножив выражение 5.59 на 5.60 получим формулу, которая выражает пространственный спектр в плоскости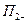 
, т.е. непосредственно перед плоскостью П2:
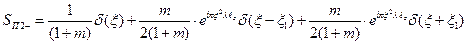(5.61)
Здесь в показателе экспоненты мы записали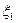 
, а не 
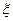, т.к. в точках, отличных от 
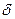-функция равна нулю.
В плоскости П2 световая волна взаимодействует с движущейся фазовой решеткой, моделирующей ПАВ. При этом амплитуду волны следовало бы умножить на функцию пропускания решетки. Однако, поскольку мы оперируем с пространственными, следует выполнить операцию свертки двух функций: 
и пространственного спектра функции в плоскости П2:
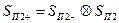, (5.62)
где 
(5.63)
Так как пространственные спектры и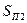 
представлены рядами в виде:
, (5.64)
, (5.65)
то свертка этих функций будет выражена следующей двойной суммой:
= 
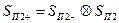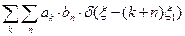(5.66)
Здесь число m=k+n можно рассматривать как номер дифракционного порядка в дифракционной картине на выходе оптической схемы. Если на выходе этой схемы выделить дифракционный порядок, соответствующий компоненте спектра с номером m, то эту компоненту можно представить в виде:
, (5.67)
где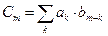 
(5.68)
Проведем расчет коэффициентов для схемы с ОДР амплитудного типа. В данной схеме коэффициенты 
и 
имеют только по три ненулевых компонента. С учетом формул 5.61 и 5.63 запишем:
|
|
|
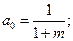
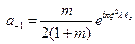(5.69)
; 
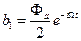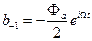(5.70)
Для нулевого дифракционного порядка с учетом последних формул получим выражение:
= 
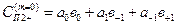(5.71)
Формулу для расчета коэффициента интенсивности нулевого порядка дифракции получим, умножив формулу (5.71) на комплексно сопряженную:
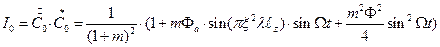(5.72)
Анализируя это выражение:
· При 
в нулевом порядке отсутствуют колебания с частотой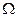 
, однако, при 
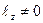колебания мощности с частотой 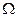в нулевом порядке могут наблюдаться.
· Если расстояние 
, то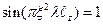 
, и тогда мы имеем максимальную амплитуду колебаний с частотой 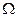в нулевом порядке.
· Мощность постоянной составляющей излучения в нулевом порядке составляет 
от мощности зондирующего излучении.
Для первого дифракционного порядка получим выражение:
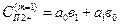(5.73)
С учетом формул (5.69) и(5.70) получим:
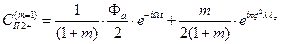(5.74)
Формулу для расчета коэффициента интенсивности нулевого порядка дифракции получим, умножив формулу (5.74) на комплексно сопряженную:
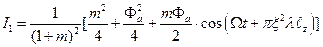(5.75)
Для минус первого дифракционного порядка (m= -1) аналогичные формулы имеют вид:
= 
(5.76)
(5.77)
Сравнив полученные выражения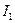 
, 
, 
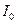можно сделать следующие выводы:
· колебания мощности в минус первом дифракционном порядке на выходе оптической схемы находятся в противофазе по отношению к колебаниям мощности в первом порядке дифракции.
· Амплитуда не зависит от расстояния между ОДР и ПАВ. Однако следует заметить, что этот вывод справедлив только в рамках модели,в которой зондирующая волна плоская, с бесконечным размером волнового фронта, а размеры периодических решеток также неограничены. В реальной схеме, где размеры зондирующего пучка ограничены, амплитуда колебаний мощности уменьшается при увеличении расстояния между ОДР и ПАВ.
· Фазы колебаний мощности в первых порядках дифракции изменяются при изменении расстояния между ОДР и ПАВ по линейному закону.
|
|
|
