Анализ схемы оптического зондирования ПАВ с опорной дифракционной решеткой фазового типа

Рассмотрим схему ОЗ с ОДР, в которой в качестве ОДР применена стационарная решетка фазового типа, функция модуляции фазы которой описывается формулой (5.15) (ступенчатая форма типа меандра). Прочие условия задачи остаются аналогичными условиям предыдущей задачи, в которой качестве ОДР применялась амплитудная решетка.

Ставятся следующие задачи: исследовать колебания интенсивности в низших дифракционных порядках, найти выражения, связывающие амплитуду и фазу колебаний мощности в дифракционных порядках с амплитудой и фазой акустической волны, а также с параметрами ОДР.

Решение. Разложим функцию пропускания фазовой ОДР в ряд Фурье, по гармоникам пространственной частоты x ₁.

, (5.35)

где 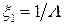, а коэффициенты разложения определяются формулами

. (5.36)

Подставив (5.15) в формулу (5.36), получим следующие формулы:

для нулевого порядка:

; (5.37)

 

для первых порядков:

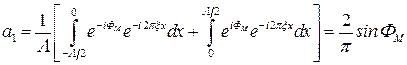, (5.38)

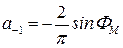. (5.39)

Общая формула для всех порядков, кроме нулевого:

. (5.40)

Используем представление функции пропускания опорной решетки в виде ряда Фурье (5.35), и подставим выражение (5.35) в формулу (1.11). В результате получим выражение для расчета пространственного спектра функции опорной дифракционной решетки в виде бесконечного ряда:

(5.41)

В общем случае функция (5.15) может иметь сдвиг относительно начала координат на величину х_о. Тогда коэффициенты ряда Фурье (5.35) получат дополнительные множители вида и пространственный спектр (5.41) примет вид:

(5.42)

Функция пропускания волны также может быть представлена в виде ряда

, (5.43)

где в соответствии с формулой (1.79)коэффициенты могут быть выражены через функции Бесселя:

. (5.44)

Здесь для сокращения последующих выражений мы отбросили начальную фазу ПАВ. С точки зрения анализа схемы с ПАВ формула (5.44) содержит избыточную информацию. Впоследствии, учитывая малую глубину модуляции волнового фронта в результате взаимодействия с ПАВ, достаточно будет оставить только три члена ряда, содержащие , , , а остальные отбросить, как это делалось нами ранее.

Однако на данном начальном этапе анализа мы проведем вывод некоторых формул в общем виде. Пространственный спектр функции пропускания волны (5.43) имеет вид:

. (5.45)

Следуя ранее разработанной схеме решения задачи, мы найдем пространственный спектр системы ОДР + ПАВ как свертку спектров (5.45) и (5.41)

(5.46)

Обозначим k + n = m, запишем выражение (5.46) в виде:

, (5.47)

где

. (5.48)

Индекс т=(k+n) имеет смысл номера дифракционного порядка.

Далее следует вычислить коэффициенты интенсивности для выбранных порядков дифракции:

. (5.49)

Далее из общего выражения (5.48) получим конкретные формулы для расчета коэффициентов интенсивности нулевого и первых порядков. Будем рассматривать схему, в которой бегущая решетка – фазовая с малой глубиной пространственной модуляции, а опорная решетка – фазовая прямоугольной формы.

Нулевой порядок, т = 0.

(5.50)

Находим величину

(5.51)

Как видно из полученного выражения, в нулевом порядке помимо постоянной составляющей cos²Ф_М присутствует полезный сигнал, т.е. колебания с частотой ПАВ, W.. Амплитуда этих колебаний пропорциональна Ф_а.

Коэффициент пропорциональности перед Ф_а cosW t, равный

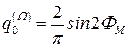, (5.52)

характеризует эффективность преобразования пространственной фазовой модуляции Ф_а в переменную составляющую интенсивности светового потока нулевого порядка с частотой, равной 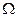. Величина этого коэффициента зависит от глубины модуляции фазовой опорной решетки Ф_М. Как видно из формулы (5.52), максимум достигается при Ф_М = 45⁰, когда sin2Ф_М = 1. При этом величина коэффициента равна:

(5.53)

Первый порядок, т = 1. Из (5.48) имеем:

(5.54)

(5.55)

Сравнивая формулы (5.55) и (5.51), можно сделать следующие выводы:

-амплитуда колебаний интенсивности с частотой W в первом дифракцион-

ном порядке вдвое меньше, чем амплитуда аналогичных колебаний в

нулевом порядке дифракции;

- коэффициент преобразования пространственной фазовой модуляции Ф_а в переменную составляющую интенсивности светового потока нулевого порядка с частотой, равной 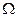, составляет:

; (5.56)

-фаза этих колебаний противоположна фазе колебаний в нулевом порядке. Задание для самостоятельной работы: получить аналогичные выражение для коэффициента интенсивности при детектировании излучения вминус первом порядке дифракции и сравнить его с предыдущими результатами.

Рекомендуется также сравнить результаты, полученные для схемы с фазовой ОДР, с ранее полученными результатами для схемы зондирования с применением амплитудой ОДР.

 

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: