 |
Анализ схемы зондирования с амплитудой гармонической ОДР
|
|
|
|
Рассмотрим вначале пространственный спектр на выходе схемы, в которой размеры акустической волны и опорной дифракционной решетки не ограничены и система освещается плоской оптической волной:
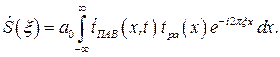(5.16)
Подставляя в (5.16) выражения (5.13) и (514), получим:
(5.17)
Перемножив выражения в круглых скобках и интегрируя (5.17), получим следующее выражение, содержащее d -функции:
(5.18)
В реальной оптической схеме зондирование производится ограниченным пучком с распределением по апертуре f (x), с пространственным спектром F (x). Выражение, описывающее зондирование ограниченным пучком, получим путем свертки спектра (5.18) со спектром функции зондирующего пучка:
(5.19)
В результате свертки получим выражение (5.18), в котором вместо d -функций будут функции 
. (5.20) Каждое слагаемое выражения (5.20) описывает величину и распределение амплитуды излучения в одном из дифракционных порядков. Здесь, в частности, в случае амплитудной гармонической ОДР коэффициенты равны:
(5.21)
. (5.22)
. (5.23)
Выделим один из дифракционных порядков, найдем распределение интенсивности и проинтегрируем по пространственному спектру в пределах той части спектра, которая соответствует пространственным частотам, которые проходят через диафрагму. Если, например, диафрагма – щель, пропускающая пространственные частоты от - xg до xg, то соответствующую мощность, прошедшую через диафрагму с единичной длиной, можно выразить:
. (5.24)
(5.25)
Записав выражения (5.24), (5.25), мы предположим, что дифракционные порядки хорошо разделяются в пространстве. Тогда в диафрагму, установленную в районе выбранного порядка (например, нулевого или первого), попадает излучение только этого порядка, а проникновение излучения из соседних порядков отсутствует. Для этого необходимо, чтобы ширина функции F (x) была значительно меньше, чем расстояние между соседними порядками, т.е. x 1. Далее покажем, что в некоторых случаях нет необходимости вычислять интеграл 
. Допустим, что функция достаточно узкая по сравнению с шириной диафрагмы и практически вся мощность, заключенная в дифракционном порядке, попадает в пределы диафрагмы. Тогда различие между интегралами и 
будет очень мала. Это позволяет условно заменить интегралы в пределах диафрагмы на интегралы в бесконечных пределах. Далее напомним, что из теоремы Парсеваля следует:
|
|
|
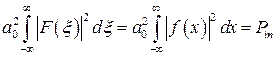. (5.26) Здесь 
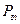–мощность зондирующего пучка на входе оптической схемы.
Тогда из выражений (5.24) – (5.26) следует, что:
(5.27)
(5.28)
Следовательно, коэффициенты I 0, I 1, 
– это нормированные мощности дифракционных порядков, которые равны отношениям соответствующих мощностей в дифракционных порядках к мощности зондирующего излучения на входе оптической схемы.
Для схемы с амплитудой ОДР получим:
в нулевом порядке:
(5.29)
Второе слагаемое содержит 
и является членом второго порядка малости. Если отбросить второе слагаемое, то в нулевом порядке остается только постояннаясоставляющаяи не содержится колебаний с частотой ПАВ.
Для первых порядков (т = +1, т = -1) получим:
(5.30)
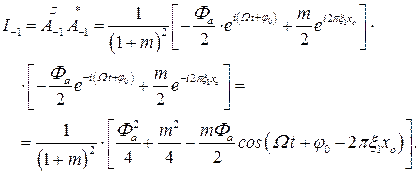(5.31)
Проанализируем полученные выражения (5.30) и (5.31).
· Оба выражения содержат постоянную составляющую и переменную составляющую на частоте ПАВ.
· Амплитуда переменной составляющей пропорциональна Фа, т.е., другими словами, амплитуда колебаний пропорциональна амплитуде бегущей ПАВ. Это позволяет производить линейное детектирование и измерение амплитуды ПАВ. Переменная составляющая 
и 
является полезным сигналом.
· Как видно из формул (5.30) и (5.31), колебания интенсивности света с частотой ПАВ в +1 и -1 дифракционных порядках происходят в противофазе.
|
|
|
· Фаза переменной составляющей зависит от фазы ПАВ,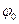 
.
· Это свойство схемы позволяет проводить не только измерения амплитудных распределений, но и фазовых распределений ПАВ.
· Фаза переменной составляющей линейно зависит от положения опорной дифракционной решетки. При смещении ОДР вдоль оси 0 х на величину 
фазовый сдвиг изменится на величину
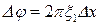. (5.32)
· При фотодетектировании излучения любого из первых порядков дифракции мы получим фототок, в котором наряду с постоянной составляющей будет присутствовать переменная составляющая, амплитуда которой пропорциональна амплитуде ПАВ, а фаза колебаний линейно связана с фазой ПАВ в точке зондирования. Это свойство схемы позволяет проводить не только измерения амплитудных распределений, но и фазовых распределений ПАВ.
Выразим величину амплитуды переменной составляющей мощности в первом порядке дифракции 
из формул (5.27) и (5.30):
(5.33)
В этой формуле выделен коэффициент эффективности 
, который зависит только от свойств дифракционной решетки и характеризует эффективность преобразования амплитуды бегущей фазовой модуляции 
в амплитуду полезного сигнала . Для данного типа решетки имеем:
(5.34)
При m=1 получим максимальное значение =0,125.
|
|
|
