 |
Тогда из второго уравнения находим вначале
|
|
|
|
.
Из первого уравнения
.
Рассмотрим узел 3.
Для этого узла уместно вспомнить правило: если в узел сходятся 4 усилия (стержня), попарно лежащие на одной прямой (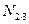
и 
; 5(кн) и 
), то усилия в этих стержнях равны между собой по величине и по знаку, т. е.
;
.
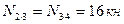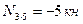Следовательно, узел 3 мы не вырезаем.
Вырезаем узел 5 (рис. 17б).
;
,
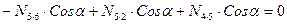или
.
;
,
или
.
Решая совместно полученные 2 уравнения
,
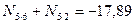, находим:
,
.
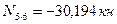Вырезаем узел 2 (рис. 18).
; 
.
; 
.
Из первого уравнения определяем
.
Из второго:
.
Узел 6 (рис. 19).
; 
,
или
.
.
; 
,
или
.
Приведем подобные и получим:
;
.
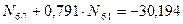Из решения полученной системы:
кн;
кн.
Узел 1 (рис. 20).
; 
,
или
.
Направлением реакции Н1 мы ошиблись.
; 
,
или
.
Последний вырезается узел 7 (рис. 21).
; 
;
(кн).
; 
;
(кн).
Как видим, для консольной фермы опорные реакции могут определяться в последнюю очередь.
Способ сквозного сечения.
При таком подходе мы имеем три уравнения статического равновесия. Это позволяет проводить сечение, разрезая по трем неизвестным усилиям (стержням). Это могут быть сечения 1–1; 2–2; 3–3; 4–4; 5–5. Сечение 5-5 равносильно вырезанию узла 4.
Рассекая ферму, впоследствии можем рассматривать равновесие одной из ее полученных частей (правой или левой).
Сечение 1-1 (правая часть фермы – рис. 22).
Используя одно из уравнений статики, определим искомое усилие.
Усилие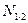 
; 
;
.
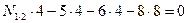Усилие 
; 
;
. (
.
Усилие 
; 
;
(кн).
Сечение 2-2 (правая часть фермы - рис. 23).
Усилие 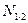нами уже определено из сечения 1-1.
Усилие 
; 
;
.
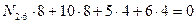Усилие 
.
; 
;
(кн).
Сечение 3-3 (вновь правая часть фермы – рис. 24).
Усилие 
.
; 
;
.
Усилие 
.
; 
;
(кн).
Сравнивая значения усилий, вычисленные двумя способами, видим небольшую разницу, связанную с погрешностью вычислений (табл. 1).
|
|
|
Таблица 1
| Усилия |
|
|
|
|
|
|
|
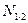
| Способ вырезания узлов | 12,304 | 16,0 | -30,194 | -15,50 | -41,752 | 14,612 | 27,0 |
| Способ сквозного сечения | 12,304 | 16,0 | -30,20 | -15,50 | -41,759 | 14,615 | 27,0 |
1.3 Многодисковая рама (рис. 25)
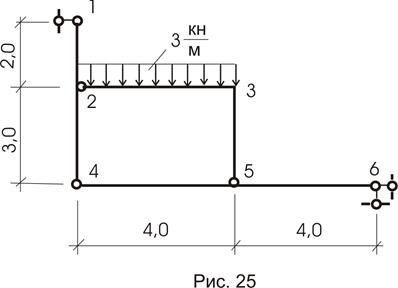
Кинематический анализ дает:
Конструкция неизменяемая и неподвижная. Определение опорных реакций в связях (шарнирах) проведем расчленением конструкции на ее составляющие элементы (другие приемы здесь неприемлемы).
1 диск (элемент) – рис. 26а.
Составляем для 1 элемента уравнения статики:
; 
.
; 
.
; 
.
2 диск (элемент) – рис. 26б.
; 
.
; 
.
; 
.
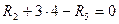3 диск (элемент) – рис. 26в.
; 
.
; 
.
; 
.
Систему уравнений представим в матричной форме:
.
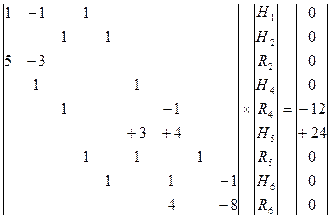Решение системы дает:
кн; 
кн; 
кн;
кн; 
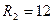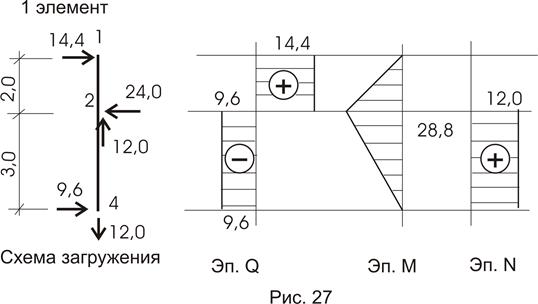
кн;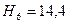 
кн;
кн; 
кн; 
кн.
Эпюры внутренних усилий строим по элементам (рис. 27, 28, 29), а потом объединяем в одно целое (рис. 30). Нужно помнить, что в схемах загружения усилия в связях прикладываем с учетом их знака: если получили знак минус, то направление усилия меняем на противоположное.
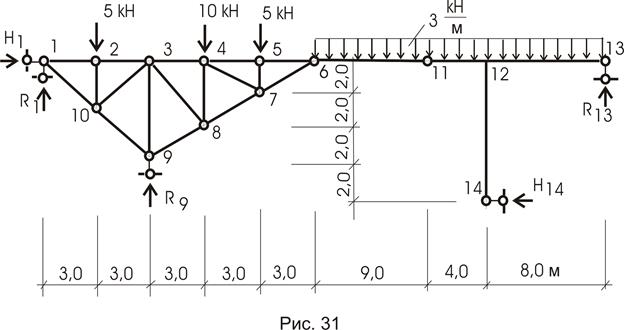
1.5 Комбинированная конструкция
Комбинированные конструкции – конструкции, состоящие из сочетания рам, балок, ферм. Для примера рассмотрим конструкцию, показанную на рисунке 31 (конструкция мостового перехода).
Расчет:
1. Кинематический анализ.
Для конструкции в целом
.
.
Расчленим конструкцию на ее элементы:
1-ый элемент – ферма
.
Ферма - геометрически неизменяемая конструкция (диск), опирающаяся на 3 опорных стержня, следовательно, является основной конструкцией. Балка и рама (второй и третий элементы) крепятся к ферме с помощью связей – шарнирами 6 и 11.
2. Опорные реакции (усилия) в связях
Расчленим конструкцию на три элемента: ферму, балку, раму.
1- ый элемент (рис. 32)
; 
.
; 
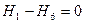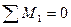или 
.
; 
или 
.
2 ой элемент (рис. 33а)
; 
.
; 
или 
(кн).
; 
.
|
|
|
Отсюда находим 
; из 2 уравнения 
.
3-ий элемент (рис.33б)
; 
.
; 
или 
.
; 
.
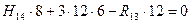Отсюда 
; 
; 
; 
.
Усилия в связях 2 и 3 элементов определены, что позволит определить и усилия в связях 1 элемента:
.
Из третьего уравнения:
,
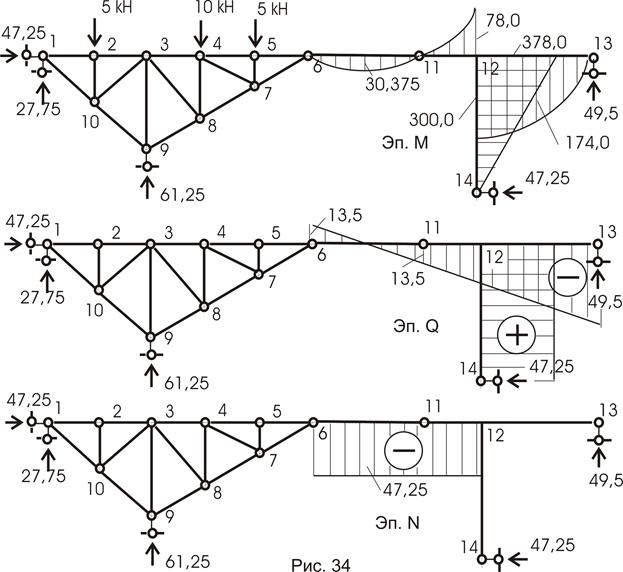
из второго:
; 
.
Знание усилий в связях позволяет одним из разобранных путей построить эпюры внутренних усилий в балке и раме (рис. 34) и определить усилия в стержнях фермы (таблица 2).
Таблица 2
| стержень | 1-2 | 2-3 | 3-4 | 4-5 | 5-6 | 6-7 | 7-8 | 8-9 |
| величина усилия | -19,5 | -19,5 | -23,25 | -26,98 | -26,98 | -24,32 | -28,82 | -36,31 |
| стержень | 9-10 | 1-10 | 2-10 | 3-10 | 3-9 | 3-8 | 4-8 | 4-7 | 5-7 |
| величина усилия | -42,78 | -39,25 | -5 | 3,53 | -10,85 | 10,44 | -12,5 | 4,50 | -5 |
Линии влияния
Линия влияния (л. в.) – это график изменения одного усилия (опорной реакции, реакции в связи, изгибающего момента, перерезывающего и продольного усилий) в определенном месте (сечении) конструкции от единичной безразмерной силы, которая движется по конструкции без ускорения, сохраняя при этом постоянное направление.
Линии влияния простых балок.
Рассмотрим простую балку на двух опорах (рис. 35а). Загружаем ее единичной силой Р = 1. Поскольку сила двигается по балке (скажем вертикального направления), то ее местоположение зафиксируем координатой х от опоры А.
Построим л. в. для опорной реакции RA.
Вычислим величину RA, рассмотрев уравнение статики 
.
;
.
Из выражения RA видим, что величина опорной реакции меняется по линейному закону. Поэтому можно задать два сечения х и по этим величинам RA построить график изменения реакции RA.
При 
, 
.
При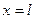 
(т. е. сила Р = 1 будет находиться на опоре В) 
.
Откладывая эти значения RA на одном графике и соединяя их прямой (рис. 35б), получим л. в. RA в пределах длины балки. Когда сила Р = 1 будет находиться в точке С, величина RA может быть вычислена из подобия треугольников или аналитически из полученной ранее формулы:
.
Читателю предлагается самостоятельно построить л. в. Rb и сравнить с графиком, показанном на рисунке 35в.
Разберем построение л. в. для Мк. Сечение «К» на расстоянии 4.0 м от опоры А (рис. 36а).
Поскольку Р = 1 двигается по балке, то она может оказаться как слева от сечения «К», так и справа от него. Необходимо рассмотреть оба положения нагрузки относительно сечения «К».
|
|
|
а) Р = 1 слева от сечения «К» (как показано на рис. 36а).
Изгибающий момент в сечении «К» можно подсчитать как от левых, так и от правых сил. От правых сил момент подсчитать удобнее – меньше слагаемых (меньше сил):
.
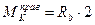Из этого выражения следует, что 
.
Следовательно, нужно построить л.в. Rb и все ее ординаты увеличить в 2 раза (рис.36б), но этот график будет справедлив только слева от сечения «К», т. е. там, где находится груз Р = 1. Эта прямая л.в. МК носит название – левая прямая. Рассмотрим второе положение Р = 1.
б) Р = 1 справа от сечения «К».
Момент в сечении удобнее подсчитать от левых сил (меньше сил на этой части балки):
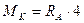или 
,
т. е. следует построить л. в. RA, ординаты которой следует увеличить в 4 раза, и этот график будет справедлив только справа от сечения “К” – правая прямая л.в. МК (рис. 36в).
Для получения полного графика л. в. МК совмещаем на одной оси обе прямые (левую и правую) л. в. МК (рис. 36г).
По такому же принципу строятся и л. в. для QK (рис. 36д) и других усилий.
Рассмотрим консольную балку (рис. 37). Построим графики изменения (л. в.) опорных реакций и внутренних усилий в сечении «К».
Линии влияния RA..
Реакция данной опоры определится из уравнения статики
; 
или .
Обратим внимание - в уравнение не вошла координата х. Следовательно, реакция опоры А постоянная, где бы ни находилась сила Р = 1 (рис. 37б).
Линия влияния HA..
Уравнение 
дает, что 
.
Линия влияния М A
Из уравнения 
получаем, что 
, откуда 
.
Знак минус говорит о том, что направление реактивного момента мы выбрали неверно, а само значение МА зависит от координаты х.
При 
.
При 
(где l – вылет консоли).
Линия влияния МА приведена на рис. 37в.
Линия влияния QK (перерезывающая сила в сечении К).
Рассмотрим положение груза Р = 1 слева от сечения (рис.37г).
Перерезывающую силу QK удобнее вычислить от правых сил, тогда
.
Левая прямая справедлива от заделки до сечения К (рис. 37е).
Когда груз Р = 1 окажется справа от сечения К (рис.37д), перерезывающую силу опять вычислим от правых сил:
.
Вновь заметим – величина QK не зависит от положения нагрузки на этом участке, т. е. QK – постоянная (рис.37е) и правая прямая справедлива от сечения К до конца консоли. В сечении К на графике л.в. наблюдается скачок на величину Р = 1.
|
|
|
Линия влияния МК (изгибающий момент в сечении К).
Подход к построению л.в. МК такой же, как и для QK. Предлагается проделать эти построения читателям самостоятельно и результаты сравнить (рис. 37ж).
Линии влияния усилий в ломаных стержнях (рамах).
Рассмотрим простейшую раму (рис.38). Будем считать, что Р = 1 двигается по горизонтальному стержню 2-3 и направлена вертикально.
Поскольку Р = 1 двигается по линии 2-3, то все графики строим по проекции этой линии (рис. 38).
Линия влияния Н1
Запишем выражение для определения Н1:
; 
, откуда находим 
.
При 
;
.
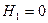График изменения Н1 показан на рисунке 38б.
Линия влияния Н3
; 
, откуда 
.
Знак минус указывает, что направление выбрано нами неудачно. Сменим его на противоположное. Другими словами, величина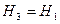 
.
Линия влияния R3
: 
; 
.
Это означает, что величина реакции R3 не зависит от положения нагрузки (рис. 38в).
Линия влияния M21 (момент в сечении 2 участка 2-1)
Величину изгибающего момента запишем как сумму моментов нижних сил, т. е. 
или величина момента меняется так же, как л.в. Н1, ординаты которой умножаются на 4 (м) (рис. 38г).
Линия влияния Q21 (перерезывающая сила в сечении 2 участка 2-1)
.
Уравнение говорит само за себя (рис. 38д).
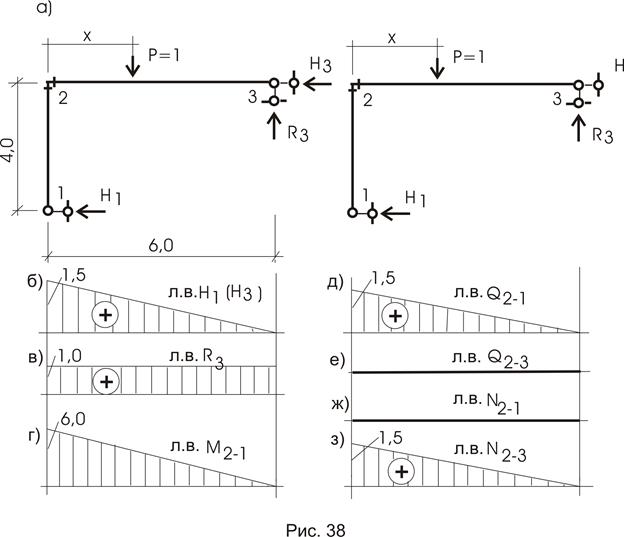
Линия влияния Q23 (перерезывающая сила в сечении 2 участка 2-3)
.
Здесь нужно считать, что сечение в узле 2 стержня 2-3 располагается бесконечно близко к узлу 2 (рис. 38е).
Линия влияния N21 (продольная сила в узле 2 участка 2-1) (рис. 38ж).
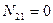(из проекции на ось стержня 2-1).
Линия влияния N21 (продольная сила в узле 2 участка 2-3) (рис. 38з).
(из проекции на ось стержня 2-3).
Линии влияния усилий в стержнях фермы
Рассмотрим ферму (рис. 39). Построим л. в. для усилий стержней 2-ой панели, а именно: N2-9; N9-8; N2-8; N2-3 и N3-8. Линии влияния опорных реакций строим по аналогии с л. в. реакций простой балки. Груз Р = 1 движется по верхнему поясу (рис.39б,в).
Линия влияния N2-9.
Наметим путь определения усилия N2-9. Проведем сечение, разрезав стержень 2-9 (рис. 40).
Рис. 39
Относительно этого сечения груз Р = 1 будет находиться слева и справа.
1) Р = 1 слева от сечения (на рисунке груз не показан).
Рассматривая правую незагруженную часть фермы, находим, используя одно из уравнений статики, усилие N2-9.
; 
или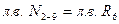 
.
Левая прямая справедлива при грузе в 1 узле.
2) Р = 1 справа от сечения 1 – 1 (правая прямая)
; 
;
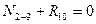(рассмотрели левую часть фермы – незагруженную).
.
Правая прямая справедлива от узла 2 до узла 5.
От узла 1 левой прямой до 2 узла правой прямой проводим передаточную прямую (рис. 40б).
|
|
|
Линия влияния N2-3.
Проведем сечение по стержням 2–3, 2-8, 9-8 и при нахождении усилия N2-3 будем пользоваться суммой моментов относительно узла 8.
а) Груз Р = 1 слева. Рассматриваем равновесие правой части.
; 
.
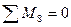Отсюда 
.
Линию влияния R6 мы увеличиваем в 
раз (рис. 40в). Левая прямая справедлива от узла 1 до узла 2.
б) Груз Р = 1 справа (правая прямая).
Рассматриваем равновесие левой части.
; 
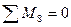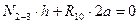
или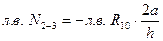 
.
Правая прямая (рис. 40в) справедлива от узла 3 до узла 5.
Между 2 узлом левой прямой и 3 узлом правой прямой проходит передаточная прямая, в данном случае совпадающая с левой прямой.
Линия влияния N2-8.
Используем уже проведенное сечение. В качестве исходного уравнения примем сумму проекций на ось «y».
а) Груз Р = 1 слева.
; 
.
Отсюда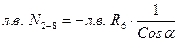 
(рис. 40 г).
График справедлив только от узла 1 до узла 2.
б) Груз Р = 1 справа от сечения.
; 
.
(рис. 40г).
Правая прямая 
будет справедлива от узла 3 до узла 5.
От узла 2 левой прямой до узла 3 правой прямой проводится передаточная прямая. Отметим особенность: для раскосов передаточная прямая занимает положение, близкое перпендикуляру к данному раскосу.
Линия влияния N9-8
Для этого усилия основным уравнением примем 
.
а) Р = 1 слева (левая прямая)
; 
.
(рис. 40д).
б) Р = 1 справа (правая прямая)
, 
.
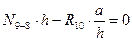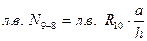(рис. 40д).
Линия влияния N3-8 (рис. 40ж).
Для определения данного усилия воспользуемся вырезанием узла 3. Расположение стержней, сходящихся в узел 3, попадает под частный случай: если в узел сходятся три стержня, два из которых лежат на одной прямой, то при отсутствии нагрузки в этом узле усилие в отдельно стоящем стержне
(N3-8) равно нулю. Следовательно, если сила будет находиться в узлах 1, 2, 4, 5, усилие 
.
Если узел 3 будет загружен силой Р = 1, то 
.
От узла 2 до узла 8 и от узла 3 до узла 4 на л.в. N3-8 будут занимать место передаточные прямые (рис. 40ж).
Далее читателям предлагается самостоятельно построить линии влияния для усилий в стержнях фермы и результаты сравнить с представленными решениями (рис. 41).
Линии влияния усилий в двухдисковой конструкции
Построения рассмотрим на примере двухдисковой рамы (рис. 42).
Линии влияния опорных реакций.
Линия влияния R1.
Вычисляем опорную реакцию R1:
; 
.
При Р = 1 слева от шарнира 3:
; 
.
При Р = 1 справа от шарнира 3:
; 
.
Решение системы 2-х уравнений с 2-мя неизвестными при Р = 1 слева от шарнира 3:
;
;
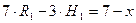дает 
. Придавая координате «х» крайние значения на этом участке, получим величину R1:
при 
,
.
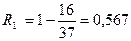При Р =1 справа от шарнира 3 получим систему двух уравнений:
;
,
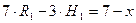решение которой дает: 
,
при 
;
;
.
График изменения 
смотрите на рис.42б.
Линия влияния Н1
Из полученных ранее уравнений при известном значении R1 находим величину Н1:
При Р = 1 слева от шарнира 3 
;
при 
;
.
При грузе Р = 1 справа от шарнира 3 
;
при 
;
;
.
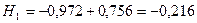По полученным значениям линия влиянии Н1 построена на рисунке 42в.
Линия влияния Н6.
Из общего уравнения равновесия конструкции:
; .
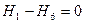Откуда следует, что 
, и следовательно, 
(рис. 42в).
Линия влияния R6.
Воспользуемся уравнением равновесия всей конструкции:
. 
.
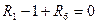Отсюда 
.
Линия влияния R6 показана на рисунке 42г.
Линии влияния внутренних усилий
Наметим сечения в узле 4 на стержне 4 - 6; в узле 4 на участке 4 - 3; в узле 4 на участке 4 – 5 (рис. 43а).
Сечение 4 на участке 4 – 6.
Линия влияния Q4-6.
Величина усилия Q4-6 вычисляется из условия равновесия нижней части (стержень 4-6):
.
Обратим внимание, что величина перерезывающей силы (Q4-6) от положения силы Р = 1 не зависит, следовательно, 
(рис. 42д).
Линия влияния N4-6.
Усилие N4-6 вычисляется как сумма всех сил на ось стержня, располагающегося ниже сечения 4 участка 4 - 6.
и, поскольку величина N4-6 не зависит от координаты х, можем утверждать: 
(рис. 42е).
Линия влияния М4-6.
Изгибающий момент в сечении 4 участка 4 – 6 вычисляется:
и опять - таки не зависит от места расположения Р = 1. Таким образом, 
меняется так же, как и 
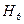, но все ординаты л.в. Н6 увеличиваются на 4 (м), т.е.. 
(рис.42ж).
Сечение 4 на участке 4 – 3 – 2.
Линия влияния Q4-3 (рис. 43б).
Величина перерезывающей силы в сечении 4 участка 4 – 3 – 2 (
) будет зависеть от положения силы Р = 1.
Сила Р = 1 слева от сечения 4.
.
Получили так называемую левую прямую.
Сила Р = 1 справа от сечения 4 – 3.
правая прямая.
Линия влияния N4-3 (рис. 43в).
Независимо от положения нагрузки Р = 1, величина N4-3 будет равна либо Н1, либо Н6, т. е.
.
Линия влияния М4-3 (рис. 43г).
Сила Р = 1 слева от сечения: 
(левая прямая).
Сила Р = 1 справа от сечения.
Здесь возможны два варианта вычисления:
а) 
, т. е. 
;
б) Силу Р = 1, находящуюся справа от сечения 4 стержня 4 – 3, зафиксируем ординатой х от узла 4 (рис. 43а). Тогда
или 
.
Линия влияния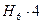 
уже построена. Остается при х = 2 добавить к значению –0,864 величину 2, т. е.:
; 
;
; 
.
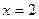Для усилий сечения 4 участка 4 – 5 линии влияния строятся как для консоли (рис. 43 д,е,ж). Предлагаем построить их самостоятельно.
Вычисление усилий по линиям влияния
Значение усилия может быть подсчитано от заданного вида загружения по линии влияния, построенной для этого усилия, по формуле:
,
где:
Рi - величина сосредоточенной нагрузки;
i – порядковый номер нагрузки;
yi -ордината линии влияния под силой Рi;
q - величина равномерно распределенной нагрузки;
лв - площадь линии влияния на участке приложения равномерно распределенной нагрузки.
Обратимся к примеру (рис. 44)
Вычислим величину реакции опоры С. Значение силы 15 кн умножим на значение линии влияния под силой (0,5) и получим:
.
Для сравнения нетрудно подсчитать реакцию из уравнения: изгибающий момент в шарнире В правых сил равен нулю:
, откуда находим R с = 7,5 кН.
Аналогично находим:
.
1.6 Определение перемещений
Перемещения точек конструкций и их элементов вычисляются по формуле Мора:
.
В выражении 
первые три слагаемые определяют перемещения точек от внешней нагрузки. Причем, из них учитываются для той или иной конструкции все три слагаемые (арочные конструкции) или одно слагаемое (ферма – слагаемое с N, рама – слагаемое с М).
Четвертое слагаемое в выражении определяет перемещения точек от осадки (перемещения) опор. И последние два слагаемых определяют перемещения точек от воздействия на конструкцию изменений температуры.
Рассмотрим по принципу независимости действия сил перемещения точек для различных конструкций от каждого воздействия отдельно.
Балки и рамные конструкции
Пример 1. Для балки, загруженной равномерно распределенной нагрузкой (рис. 45а), требуется определить:
1. Перемещение по вертикали точки К (
).
2. Перемещение по вертикали точки 3 (
).
3. Угол поворота точки 3 (
