 |
Окончательная эпюра моментов показана на рисунке 106.
|
|
|
|
д) Статическая проверка. Равновесие узла 1 (рис. 107) удовлетворяет. условию равновесия:
10,489 = 10,49.
Кинематическая проверка.
Выбираем основную систему метода сил и приложим в опору 2 по
вертикали силу 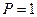 . Построим от нее М1 (рис. 108). Перемножим полученные эпюры
. Построим от нее М1 (рис. 108). Перемножим полученные эпюры 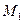 и Мок:
и Мок:
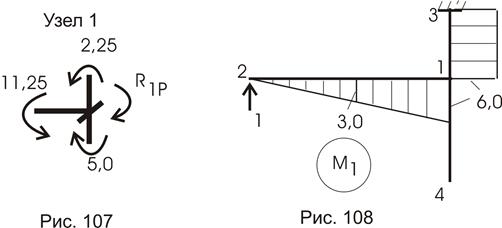




Погрешность составляет:

По эпюре Мок строим эпюру Qок уже разобранными ранее приемами (рис. 109а), по Qок построим эпюру Nок (рис. 109б).

Расчет рамы методом сил
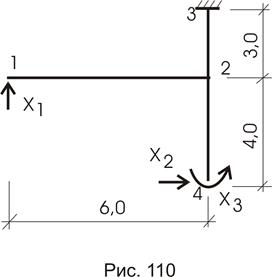
а) Основная система (варианты приводить не будем, рис. 110).
б) Канонические уравнения:



Вычисляем коэффициенты  и грузовые слагаемые -
и грузовые слагаемые -  . Эпюры моментов от единичных загружений и внешней нагрузки можно видеть на рисунке 111.
. Эпюры моментов от единичных загружений и внешней нагрузки можно видеть на рисунке 111.
Некоторые вычисления для Мр:
 (растянутые левые волокна).
(растянутые левые волокна).

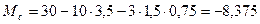 (в обоих последних случаях растянутые правые волокна).
(в обоих последних случаях растянутые правые волокна).

Для  применяем правило Верещагина:
применяем правило Верещагина:
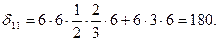

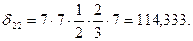
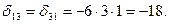
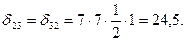



Для  используем правило Симпсона и Верещагина (для прямолинейных участков):
используем правило Симпсона и Верещагина (для прямолинейных участков):
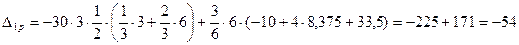 ;
;

 ;
;
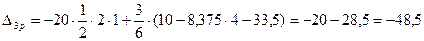 .
.
в) Решение системы уравнений:


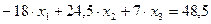
дает:  ;
;  ;
; 
г) Построение Мок.
Как и прежде  (рис. 112).
(рис. 112).
Сравнение Мок, вычисленных методом сил и методом перемещений, дает хорошие результаты. Дальнейший ход решения повторяется.
Глава 3. Расчет сооружений на устойчивость
3.1. Основные понятия
Устойчивость отдельного стержня или сооружения (конструкции) в целом есть способность стержня (конструкции) сохранять свою форму и геометрические размеры под действием внешней нагрузки.
Потеря формы стержня и его геометрических размеров происходит от нагрузки, которая называется критической. Расчет на устойчивость и направлен на определение величины этой критической нагрузки (или нагрузок).
|
|
|
Для определения величины критической силы Ркр одного стержня используется метод непосредственного интегрирования дифференциального уравнения сжато-изогнутой оси стержня. Решение этой задачи было получено Л.Эйлером в 1744 году:
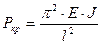 .
.
Эйлером и его последователями было показано, что величина  зависит от условий закрепления концов отдельного стержня. Это видно из таблицы 5
зависит от условий закрепления концов отдельного стержня. Это видно из таблицы 5
Использовать этот метод для совокупности стержней, представляющих конструкцию в целом, затруднительно из-за громоздкости вычислений. Были предложены статические методы: метод сил и метод перемещений (на их основе - и другие способы).
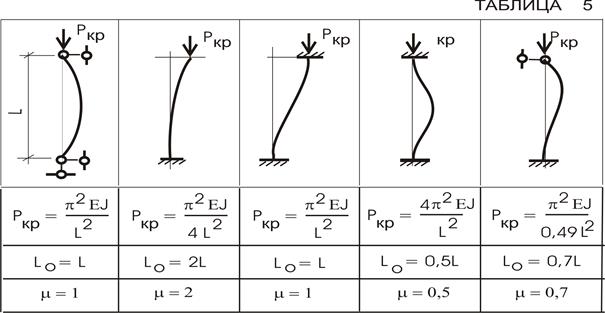
Наиболее практичным оказался метод перемещений.
Напомним: в методе перемещений в качестве неизвестных принимаются линейные и угловые перемещения  .
.
Общий вид канонических уравнений представим на примере с 3-мя неизвестными:
 ;
;
 ;
;
 .
.
Поскольку сам расчет на устойчивость предполагает прикладывать усилие вдоль стержня (стержней), то при расчете всю нагрузку, действующую на конструкцию (сооружение) (рис. 113б), распределяют по узлам.
Тогда реактивные усилия во введенных связях от внешней нагрузки будут равны нулю и система канонических уравнений становится однородной, т. е.:
 ;
;
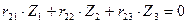 ;
;
 .
.

Такая система уравнений имеет два решения:
1) либо 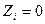 , т. е. перемещения узлов отсутствуют;
, т. е. перемещения узлов отсутствуют;
2) либо определитель системы уравнений равен нулю:

Первый случай нас не устраивает, поскольку нет перемещений – нет и вопроса устойчивости, т. к. только при наличии перемещений узлов происходит потеря устойчивости конструкции.
Остается второй случай:
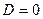 .
.
Коэффициенты  в определителе вычисляются как в методе перемещений из эпюр моментов при единичных перемещениях введенных связей, но с учетом продольного воздействия сжимающей силы
в определителе вычисляются как в методе перемещений из эпюр моментов при единичных перемещениях введенных связей, но с учетом продольного воздействия сжимающей силы  .
.
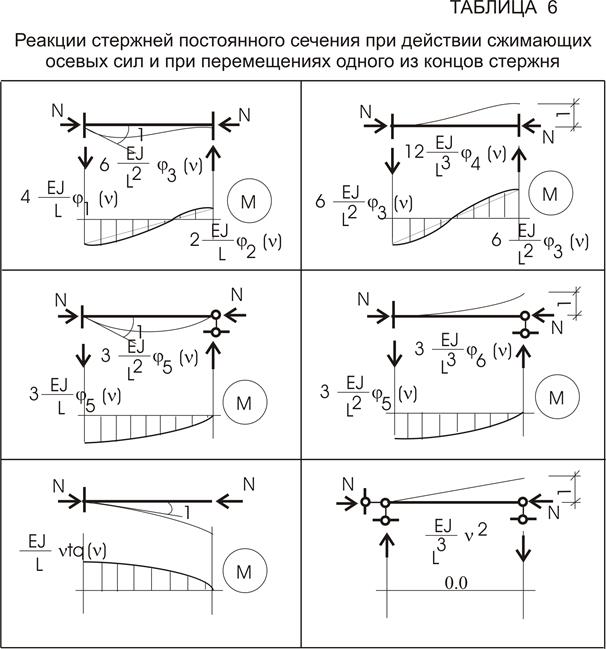
Для отдельных стержней с различными условиями опирания эти задачи решены и представлены в таблице 6.
|
|
|
Если присмотреться к величинам реактивных усилий, то заметим, что к известному значению от перемещения без влияния продольной силы добавляется сомножитель, учитывающий влияние сжимающих усилий. Значения этих функций имеют вид:
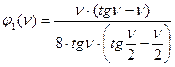 ;
;  ;
; 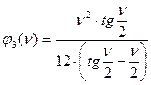 ;
;
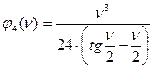 ;
;  ;
;  .
.
Функции 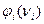 зависят от критического параметра
зависят от критического параметра  , который вычисляется по формуле
, который вычисляется по формуле
 ,
,
где 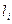 - длина
- длина  -го стержня;
-го стержня; 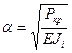 .
.
Определив все  в общем виде, подставим их в определитель. Раскроем определитель и получим уравнение устойчивости, решение которого производится методом подбора с использованием таблицы 7. Для этого назначается начальная величина
в общем виде, подставим их в определитель. Раскроем определитель и получим уравнение устойчивости, решение которого производится методом подбора с использованием таблицы 7. Для этого назначается начальная величина  , по которой определяются значения
, по которой определяются значения 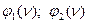 и т. д. Полученные значения
и т. д. Полученные значения  подставляются в уравнение устойчивости. Если результат вычислений не равен нулю при заданном значении
подставляются в уравнение устойчивости. Если результат вычислений не равен нулю при заданном значении  , то принимается новое значение
, то принимается новое значение  и до тех пор, пока уравнение не достигнет нуля (или будет близким к нулю). Последнее значение
и до тех пор, пока уравнение не достигнет нуля (или будет близким к нулю). Последнее значение  и есть тот критический параметр, соответствующий критической силе
и есть тот критический параметр, соответствующий критической силе  .
.
По величине  подбирается (или проверяется) длина стержня по выражению:
подбирается (или проверяется) длина стержня по выражению:
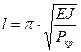 .
.
Расчетная же длина стержня  определяется из соотношения:
определяется из соотношения:
 ,
,
где μ – коэффициент, зависящий от условий закрепления концов стержня (табл. 5).
3.2 Примеры расчета
Пример 1.
Определить величину критической силы для стойки (рис. 114а) постоянной жесткости 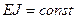 . Основная система метода перемещений для стойки показана на рис. (114б).
. Основная система метода перемещений для стойки показана на рис. (114б).
Эпюра моментов от единичного перемещения связи (угла поворота введенной заделки) с использованием таблицы 6 показана на рис. 114в. Каноническое уравнение запишется:
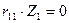 .
.
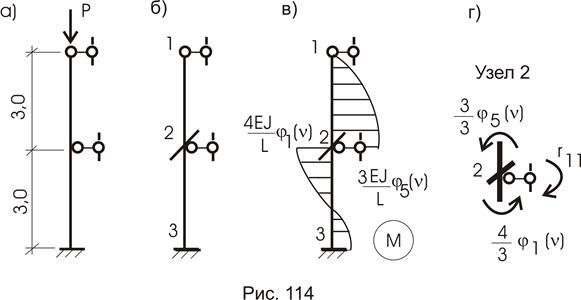
Критический параметр для обоих участков (стержней) одинаковый:
 ;
;
l = 3;  следует найти,
следует найти, 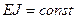 (по условию задачи).
(по условию задачи).
Величина 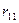 вычисляется из условия равновесия узла 2 (рис. 114г):
вычисляется из условия равновесия узла 2 (рис. 114г):
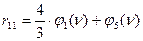 .
.
Уравнение устойчивости примет вид:

или
 .
.
Данное уравнение решаем путем подбора, используя таблицу 7 специальных функций.
Исследуя данное уравнение, замечаем, что одно из слагаемых должно быть величиной отрицательной. Из таблицы видим, что при малых значениях ( ) отрицательной будет функция
) отрицательной будет функция 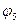 .
.
1) Принимаем  .
.
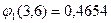 ;
;  .
.
Подставим их в уравнение устойчивости:
D = 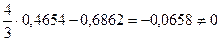 .
.
2) Примем 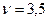 .
.
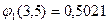 ;
; 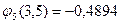 ;
;
D= 
 .
.
Решение находится между  , но ближе к 3,6 (по интерполяции).
, но ближе к 3,6 (по интерполяции).
ТАБЛИЦА 7
|
|
|
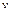
| 
| 
| 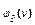
| 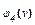
| 
| 
|
| 0,0 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
| 0,1 | 0,9997 | 1,0002 | 0,9998 | 0,9990 | 0,9993 | 0,9960 |
| 0,2 | 0,9987 | 1,0007 | 0,9993 | 0,9960 | 0,9973 | 0,9840 |
| 0,3 | 0,9970 | 1,0015 | 0,9985 | 0,9910 | 0,9940 | 0,9640 |
| 0,4 | 0,9947 | 1,0027 | 0,9973 | 0,9840 | 0,9893 | 0,9360 |
| 0,5 | 0,9916 | 1,0042 | 0,9958 | 0,9750 | 0,9832 | 0,8999 |
| 0,6 | 0,9879 | 1,0061 | 0,9940 | 0,9640 | 0,9757 | 0,8557 |
| 0,7 | 0,9836 | 1,0083 | 0,9918 | 0,9510 | 0,9669 | 0,8035 |
| 0,8 | 0,9785 | 1,0109 | 0,9893 | 0,9360 | 0,9565 | 0,7432 |
| 0,9 | 0,9727 | 1,0138 | 0,9864 | 0,9189 | 0,9447 | 0,6747 |
| 1,0 | 0,9662 | 1,0172 | 0,9832 | 0,8999 | 0,9313 | 0,5980 |
| 1,1 | 0,9590 | 1,0209 | 0,9797 | 0,8788 | 0,9164 | 0,5131 |
| 1,2 | 0,9511 | 1,0251 | 0,9757 | 0,8557 | 0,8998 | 0,4198 |
| 1,3 | 0,9424 | 1,0297 | 0,9715 | 0,8307 | 0,8814 | 0,3181 |
| 1,4 | 0,9329 | 1,0348 | 0,9669 | 0,8035 | 0,8613 | 0,2080 |
| 1,5 | 0,9227 | 1,0403 | 0,9619 | 0,7744 | 0,8393 | 0,0893 |
| π/2≈1,57 | 0,9149 | 1,0445 | 0,9581 | 0,7525 | 0,8225 | 0,0000 |
| 1,6 | 0,9116 | 1,0463 | 0,9565 | 0,7432 | 0,8152 | –0,0381 |
| 1,7 | 0,8998 | 1,0529 | 0,9508 | 0,7100 | 0,7891 | –0,1743 |
| 1,8 | 0,8871 | 1,0600 | 0,9447 | 0,6747 | 0,7606 | –0,3194 |
| 1,9 | 0,8735 | 1,0676 | 0,9382 | 0,6374 | 0,7297 | –0,4736 |
| 2,0 | 0,8590 | 1,0760 | 0,9313 | 0,5980 | 0,6961 | –0,6372 |
| 2,1 | 0,8436 | 1,0849 | 0,9241 | 0,5566 | 0,6597 | –0,8103 |
| 2,2 | 0,8273 | 1,0946 | 0,9164 | 0,5131 | 0,6202 | –0,9931 |
| 2,3 | 0,8099 | 1,1051 | 0,9083 | 0,4675 | 0,5772 | –1,1861 |
| 2,4 | 0,7915 | 1,1164 | 0,8998 | 0,4198 | 0,5304 | –1,3896 |
| 2,5 | 0,7720 | 1,1286 | 0,8908 | 0,3700 | 0,4793 | –1,6040 |
| 2,6 | 0,7513 | 1,1417 | 0,8814 | 0,3181 | 0,4234 | –1,8299 |
| 2,7 | 0,7295 | 1,1559 | 0,8716 | 0,2641 | 0,3621 | –2,0679 |
| 2,8 | 0,7064 | 1,1712 | 0,8613 | 0,2080 | 0,2944 | –2,3189 |
| 2,9 | 0,6819 | 1,1878 | 0,8505 | 0,1497 | 0,2195 | –2,5838 |
| 3,0 | 0,6560 | 1,2057 | 0,8393 | 0,0893 | 0,1361 | –2,8639 |
| 3,1 | 0,6287 | 1,2251 | 0,8275 | 0,0267 | 0,0424 | –3,1609 |
| π ≈3,14 | 0,6168 | 1,2337 | 0,8225 | 0,0000 | 0,0000 | –3,2899 |
| 3,2 | 0,5997 | 1,2462 | 0,8152 | –0,0381 | –0,0635 | –3,4769 |
| 3,3 | 0,5691 | 1,2691 | 0,8024 | –0,1051 | –0,1847 | –3,8147 |
| 3,4 | 0,5366 | 1,2940 | 0,7891 | –0,1743 | –0,3248 | –4,1781 |
| 3,5 | 0,5021 | 1,3212 | 0,7751 | –0,2457 | –0,4894 | –4,5727 |
| 3,6 | 0,4655 | 1,3509 | 0,7606 | –0,3194 | –0,6862 | –5,0062 |
| 3,7 | 0,4265 | 1,3834 | 0,7455 | –0,3954 | –0,9270 | –5,4904 |
| 3,8 | 0,3850 | 1,4191 | 0,7297 | –0,4736 | –1,2303 | –6,0436 |
| 3,9 | 0,3407 | 1,4584 | 0,7133 | –0,5542 | –1,6269 | –6,6969 |
| 4,0 | 0,2933 | 1,5019 | 0,6961 | –0,6372 | –2,1726 | –7,5060 |
| 4,1 | 0,2424 | 1,5501 | 0,6783 | –0,7225 | –2,9802 | –8,5836 |
| 4,2 | 0,1878 | 1,6037 | 0,6597 | –0,8103 | –4,3156 | –10,196 |
| 4,3 | 0,1287 | 1,6636 | 0,6404 | –0,9005 | –6,9947 | –13,158 |
| 4,4 | 0,0648 | 1,7310 | 0,6202 | –0,9931 | –15,327 | –21,780 |
| 4,4934 | 0,0000 | 1,8017 | 0,6006 | –1,0820 | –∞/+∞ | –∞/+∞ |
| 4,5 | –0,0048 | 1,8070 | 0,5991 | –1,0884 | 227,93 | 221,18 |
| 4,6 | –0,0809 | 1,8933 | 0,5772 | –1,1861 | 14,669 | 7,6160 |
| 4,7 | –0,1645 | 1,9920 | 0,5543 | –1,2865 | 7,8186 | 0,4553 |
| 3 π /2≈4,71 | –0,1755 | 2,0051 | 0,5514 | –1,2991 | 7,4038 | 0,0000 |
| 4,8 | –0,2572 | 2,1056 | 0,5304 | –1,3896 | 5,4023 | –2,2777 |
| 4,9 | –0,3607 | 2,2375 | 0,5054 | –1,4954 | 4,1463 | –3,8570 |
| 5,0 | –0,4772 | 2,3923 | 0,4793 | –1,6040 | 3,3615 | –4,9719 |
| 5,1 | –0,6099 | 2,5757 | 0,4520 | –1,7155 | 2,8130 | –5,8570 |
| 5,2 | –0,7629 | 2,7960 | 0,4234 | –1,8299 | 2,3986 | –6,6147 |
| 5,3 | –0,9422 | 3,0648 | 0,3935 | –1,9474 | 2,0668 | –7,2965 |
| 5,4 | –1,1563 | 3,3989 | 0,3621 | –2,0679 | 1,7884 | –7,9316 |
| 5,5 | –1,4182 | 3,8236 | 0,3291 | –2,1917 | 1,5455 | –8,5379 |
| 5,6 | –1,7481 | 4,3794 | 0,2944 | –2,3189 | 1,3266 | –9,1268 |
| 5,7 | –2,1803 | 5,1346 | 0,2580 | –2,4495 | 1,1235 | –9,7065 |
| 5,8 | –2,7777 | 6,2139 | 0,2195 | –2,5838 | 0,9302 | –10,283 |
| 5,9 | –3,6679 | 7,8727 | 0,1790 | –2,7219 | 0,7421 | –10,861 |
| 6,0 | –5,1594 | 10,727 | 0,1361 | –2,8639 | 0,5551 | –11,444 |
| 6,1 | –8,2336 | 16,739 | 0,0907 | –3,0102 | 0,3656 | –12,037 |
| 6,2 | –18,590 | 37,308 | 0,0424 | –3,1609 | 0,1700 | –12,643 |
| 2 π ≈6,28 | –∞ | +∞ | 0,0000 | –3,2899 | 0,0000 | –13,159 |
|
|
|
Примем  .
.
 или
или  ,
,
откуда
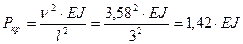 .
.
Расчетные длины стержней для обоих участков будут равны (используется табл. 1):
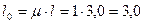 (м).
(м).
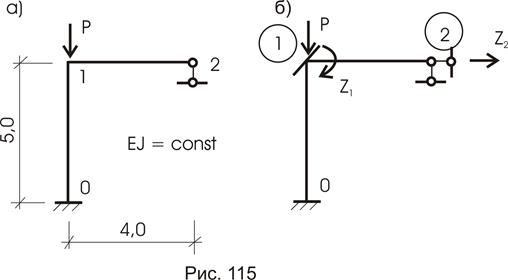
Пример 2.
Определить величину критической силы для рамы, приведенной на рисунке 115а.
Решение.
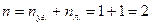 .
.
Здесь мы опускаем процесс подсчета числа неизвестных.
Основная система показана на рисунке 115б.
Система канонических уравнений запишется:

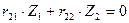 .
.
В этой системе должно быть 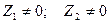 . Тогда должен равняться нулю определитель при неизвестных, т. е.
. Тогда должен равняться нулю определитель при неизвестных, т. е.
 .
.
Раскроем определитель:
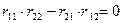 .
.
Произведем вычисления  .
.
Эпюры М1 и М2 (от единичных перемещений первой и второй связей соответственно) приведены на рисунке 116а,б.

Напоминаем: для сжатых стержней внешней нагрузкой (в нашем случае только стойка) эпюра изгибающих моментов берется из таблицы 6, а для стержней, не подвергающихся сжатию, принимается, как и в обычном методе перемещений.
Из эпюры М1 вырежем узел с первой связью (рис. 117 и здесь же показано вычисление r11).
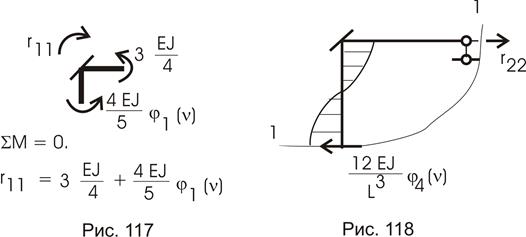
Из эпюры М2 сечением 1 – 1 определим  (рис. 118).
(рис. 118).
 ;
;  ;
;  .
.
Вырезая узел с первой связью (рис. 119), находим 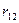 :
:
 .
.
Подставим полученные значения в уравнение устойчивости:
 .
.

Вынесем EJ. Получаем:
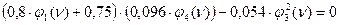 .
.
В полученном уравнении параметр устойчивости  один (т.е. для одного стержня).
один (т.е. для одного стержня).
Переходим к решению уравнения.
Принимаем  , тогда по таблице 7:
, тогда по таблице 7:
 .
.
Подставим в уравнение устойчивости:
D = 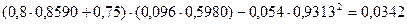 .
.
Принимаем  :
:
D =  .
.
Принимаем  :
: 
D =  .
.
Значение критического параметра находится между  и
и  с большим приближением к
с большим приближением к  .
.
Интерполируя, принимаем 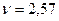 .
.
Критическая сила определится:
 .
.
Расчетная длина сжатого стержня, а именно стержня 0-1, определится:
 .
.
Пример 3.
Для заданной рамы и приложения нагрузки определить величину  и расчетные длины сжатых стержней (рис. 120а).
и расчетные длины сжатых стержней (рис. 120а).
Определяем основную систему метода перемещений (рис. 120б). Получим раму с 3-мя неизвестными. Определитель системы канонических уравнений при неизвестных приравняем нулю.
D =  ;
;

Раскроем определитель по элементам первой строки и приравняем результат раскрытия определителя нулю, т. е. получим уравнение устойчивости:
|
|
|
 .
.
Для вычисления  построим эпюры изгибающих моментов от перемещений введенных связей на единицу, используя таблицу 6 для сжатых стержней (рис. 121, 122).
построим эпюры изгибающих моментов от перемещений введенных связей на единицу, используя таблицу 6 для сжатых стержней (рис. 121, 122).
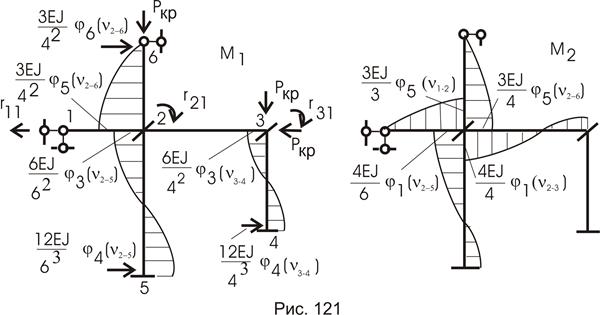
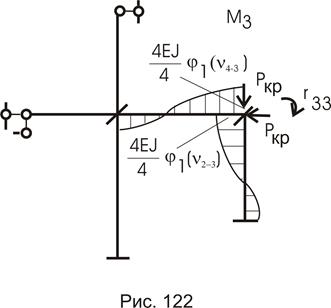
Из полученных эпюр видим, что критический параметр для стержней различный. Приведем их к одному, т.е. получим так называемые приведенные параметры  .
.
Распишем критические параметры для каждого стержня из общего выражения:
 ,
,
где, как мы уже отмечали,  .
.
При  . С учетом этого запишем:
. С учетом этого запишем:


 .
.
Примем больший критический параметр за  (можно сказать, за единичный). Тогда все другие, заметьте, будут выражаться через
(можно сказать, за единичный). Тогда все другие, заметьте, будут выражаться через  с коэффициентом меньшим единицы, а именно:
с коэффициентом меньшим единицы, а именно:
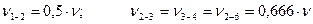 .
.
(Отметим, что это делается лишь для того, чтобы при использовании таблицы 7 не получилось так, что значения критического параметра в ней не окажется).
Вернемся к вычислению реактивных усилий -  .
.
Из эпюры М1 находим  :
:

 ;
;

 ;
;
 .
.
Из эпюры М2 находим  :
:
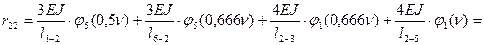
 ;
;
 .
.
Из эпюры 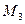 определим
определим 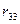 :
:
 .
.
Выпишем отдельно значения  , входящие в уравнение устойчивости:
, входящие в уравнение устойчивости:
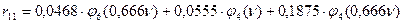 ;
;
 ;
;
 ;
;
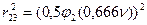 ;
;
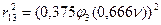 ;
;

и рядом запишем само уравнение:
 .
.
Значение критического параметра вычисляется из выражения:
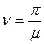 ,
,
где  , как нам известно, зависит от закрепления концов сжатого стержня (см. таблицу 5). Для первого стержня
, как нам известно, зависит от закрепления концов сжатого стержня (см. таблицу 5). Для первого стержня  , а для последнего -
, а для последнего - 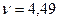 . Следовательно, значение критического параметра лежит в пределах от 3,14 до 4,49. В первом приближении примем
. Следовательно, значение критического параметра лежит в пределах от 3,14 до 4,49. В первом приближении примем  = 3.
= 3.
0,666  = 2,0; 0,5
= 2,0; 0,5  = 1,5.
= 1,5.
По таблице 7 определяем значения функций:
 ;
;  ;
;
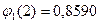 ;
; 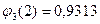 ;
;
 ;
;
 ;
; 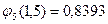 ;
;
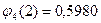 ;
; 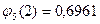 ;
;
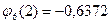 .
.
Теперь вычислим  :
:
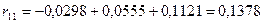 ;
;
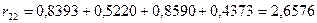 ;
;
 ;
; 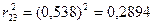 ;
;
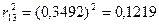 ;
;  .
.
Полученные значения подставляем в уравнение равновесия:
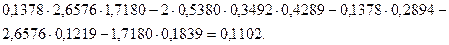 .
.
Как видим, результат не равен нулю.
Положим  ,90; 0,666
,90; 0,666  =2,6; 0,5
=2,6; 0,5  = 1,95.
= 1,95.
Значения функций:
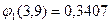 ;
; 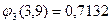 ;
;
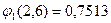 ;
; 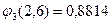 ;
;
 ;
;
 ;
; 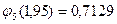 ;
;
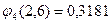 ;
;  ;
;
 .
.
Вычисляем  (промежуточные вычисления опускаем):
(промежуточные вычисления опускаем):
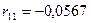 ;
; 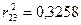 ;
;
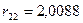 ;
; 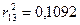 ;
;
 ;
; 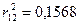 .
.
Вычисляем само уравнение:
 .
.
Интерполяция в предположении линейности уравнения дает  = 3,16.
= 3,16.
По условию закрепления стержней (табл. 5) вычисляем их расчетные длины, т.е.:
 ;
; 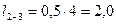 ;
;
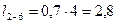 ;
;  ;
;
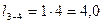 .
.
Используя расчетные длины стержней и критический параметр для них, определяем величину критических усилий (критическую нагрузку) для каждого стержня из выражения:
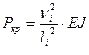 .
.
Тогда Р1-2 = 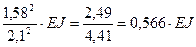 ,
,
а далее запишем только результаты:
Р2-3 = 1,102ЕJ; Р2-6 = 0,127EJ;
Р2-5 = 0,277EJ; Р3-4 = 0,275EJ.
Глава4. Расчет сооружений на динамическую нагрузку
4.1. Основные понятия
Виды динамических нагрузок
Периодическая нагрузка – нагрузка, вызванная движущимися частями стационарных механизмов (электродвигатели, турбогенераторы, различного типа станки и т.д.).
Импульсивная нагрузка – нагрузка, вызванная падающими грузами (молоты, сваебойные копры и т.д. и землетрясения).
Подвижная нагрузка – нагрузка, вызванная движением механизмов (поезда, автомобили, строительные и производственные краны и т.д.).
Перечисленные и другие виды нагрузок встречаются как в чистом виде, так и в их комбинациях.
Типы колебаний
Колебания бывают нарастающие, незатухающие и затухающие. Для нарастающих колебаний характерно нарастание по времени амплитуды – «а» и периода колебаний – Т (рис. 123). У незатухающих колебаний амплитуда и период колебаний остаются постоянными. Для затухающих колебаний характерно уменьшение по времени амплитуды и периода колебаний.
После снятия нагрузки, вызывающей колебания системы (конструкции), в ней продолжается колебательный процесс. Такие колебания называются свободными. В идеальных условиях свободные колебания не затухают. Однако на практике за счет сил сопротивления и сил трения такие колебания конструкции затухают.
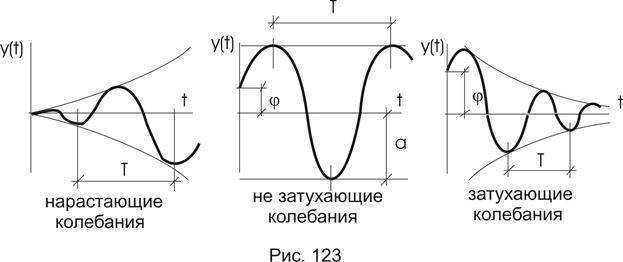
Если форма колебаний с течением времени не меняется, то такие колебания называются собственными. Название «собственные» связано с тем, что они зависят от собственных характеристик конструкции: величин масс и их распределением, жесткостных параметров, геометрии конструкции, видов опорных устройств и т.д.
Большое практическое значение имеют периодические колебания – колебания, удовлетворяющие условию:
y(t) = y(t+T),
где y(t) – перемещение массы в момент времени – t;
T - период колебаний.
Периодические колебания характеризуются:
- круговой частотой  (омега). Круговая частота (число колебаний за 2
(омега). Круговая частота (число колебаний за 2  секунд) вычисляется:
секунд) вычисляется:
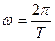 (сек-1);
(сек-1);
- технической частотой f, которая выражает число колебаний за одну секунду и вычисляется:
f =  (гц);
(гц);
- амплитудой колебаний а:
а = 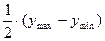 .
.
Периодические колебания, совершаемые по закону

 ),
),
называются гармоническими колебаниями, где  - фаза колебаний, а
- фаза колебаний, а  - начальная фаза колебаний.
- начальная фаза колебаний.
Понятие о массе конструкции
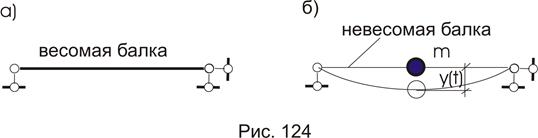
В расчетах на динамические нагрузки вес конструкции (скажем балки) распределяют по участкам, собирая его в весомую точку – массу m. Самый простой случай будет, если вес балки соберем в одну весомую точку и разместим ее в середине (рис. 124а). Значение массы подсчитывается по выражению:
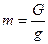 ,
,
где G – вес груза, равный весу балки, g – ускорение свободного падения.
Точка приложения массы (рис. 124б) имеет возможность перемещаться только по вертикали y(t). Тогда мы говорим - балка имеет одну степень свободы. Здесь степень свободы – количество возможных перемещений массы (масс).
Для более точного расчета вес балки можно сосредоточить в нескольких местах (рис. 125), получая балку с 2-мя, 3-мя степенями свободы и т.д. (в этих примерах углы поворота масс не учитываются).

Чем больше количество степеней свободы, тем сложнее расчет. Поэтому для каждого типа сооружения положение массы (масс) выбирается с учетом его специфики. Так, для водонапорной башни, где основная нагрузка находится наверху, массу размещают наверху (рис. 126), а для дымовой
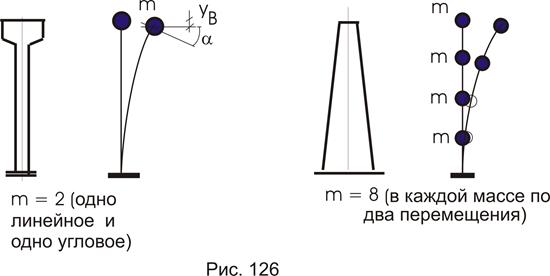
трубы использовать одну массу наверху просто нельзя, т.к. это в принципе не отражает работу трубы. В этом случае берутся несколько масс по ее высоте (рис. 126). Для рамы с тремя массами (рис. 127) мы имеем семь степеней свободы.

О методах расчета
Из методов расчета на динамические воздействия используют, в основном, два способа: статический и энергетический.
Статический способ основан на записи уравнений динамического равновесия, в которых учитываются силы инерции в виде произведения масс сооружения на ускорения, что вытекает из принципа Даламбера. Часто такие уравнения называются уравнениями движения, так как на самом деле равновесия системы нет- она колеблется.
Энергетический способ основан на применении закона сохранения энергии: сумма потенциальной и кинетической энергий упругой системы
является величиной постоянной по времени.
Наибольшее применение нашел статический способ расчета.
4.2 Расчет систем с одной степенью свободы.
Рассмотрим невесомую балку с одной массой (рис. 128а). На массу будут действовать силы (рис. 128б):

Р(t) – динамическая нагрузка;
J - сила инерции массы 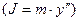 ;
;
R - сила сопротивления конструкции и внешней среды (R = Rк + Rср) ее колебаниям.
Уравнение равновесия дает:
P(t) – J - R = 0 или 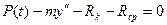 .
.
Рассмотрим свободные колебания, когда Р(t)=0 и силы сопротивления не учитываются: R=0. Тогда уравнение движения системы с одной степенью свободы записывается в виде дифференциального уравнения второго порядка:
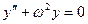 ,
,
где  2 =
2 =  - круговая частота,
- круговая частота,  - перемещение точки приложения массы при статическом воздействии единичной нагрузки в эту точку по направлению перемещения этой массы.
- перемещение точки приложения массы при статическом воздействии единичной нагрузки в эту точку по направлению перемещения этой массы.
Опустим процесс решения этого уравнения и приведем его результат для периода колебаний:
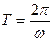 .
.
Перейдем к рассмотрению примеров.
Пример 1.
Для конструкции (рис. 129а) требуется определить круговую частоту  , период колебания Т и техническую частоту f. Дано: G = 40(кн), g = 9,81 (м/сек 2 ). Тогда m = Q/g = 4,08 (кнсек 2 ) / м.
, период колебания Т и техническую частоту f. Дано: G = 40(кн), g = 9,81 (м/сек 2 ). Тогда m = Q/g = 4,08 (кнсек 2 ) / м.
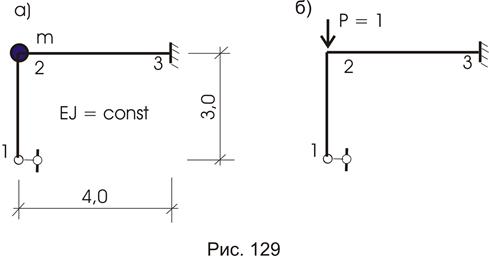
Решение.
Для определения круговой частоты  следует определить величину перемещения
следует определить величину перемещения


